SCI论文(www.lunwensci.com)
摘 要 : 数学难题主要表现为找不到解题的突破口,陷入无从下手的困境,有时认为解题思路 是正确的,但还是结果出错或思路走不到尽头,半途而废.影响这些问题的因素较多.而“看、想、 做”是解题的基本功,直接影响解题的成败.提升“看、想、做”的水平,对破解难题有重要作用.
G·波利亚所言: “掌握数学就是意味着善于解 题.”而一个题目的难易因人而言,不仅与个体是否 有充足的“粮草”有关,还与思考问题的方法和思维 方式有关.而“看、想、做”是解题的基本功,直接影 响解题的成败.下面以 2021 年浙江高考第 22 题第 (3) 问为例,从“看、想、做”进行剖析解题思路.
1 题目回放
2.1 看得清———有哪些? 是什么? 是怎样?
看是想的基础,没看清、没看准,会对解题思路 方向直接产生误判,甚至造成解题失败.因此,看清 是解题的基础,是确定解题方向的依据.俗话说 : 良
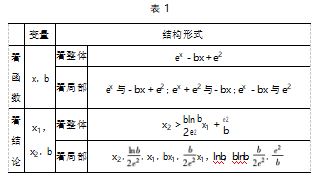
有何联系? 会产生什么作用? 见表 1.又如看图形 : 图形确定了吗? 若不定,与参数的关系怎样? 有无 过定点? 与坐标轴交点怎样? 单调性如何? 最高点 ( 最低点) 位置在哪? 图形变化趋势又是怎样? 特 别要关注函数极点(切点) 和零点变化范围.
一个数学式子,当你不去专注看它时,它只是一些字母和数字符号堆砌而成的数学式子,而当你带着思想进入到与它互动的状态时,它就成为你希望 的结果.在头脑中所构建所希望的样子是存在的,只不过被隐藏起来.
2.2 想得起——— 与谁类同? 能做什么? 还需做什么?
联想是由此及彼的思考,根据题型和所要做的 任务特点、式子结构和图形特征与储存在头脑中的 公式、概念、模式、命题、方法等,通过对比、类比、因 果、数形互化等方式进行联想,发现它们之间的关系,寻找解决思路,选择适合走向目标的解题路径.
解题往往是凭直接经验先尝试.此题要证的结
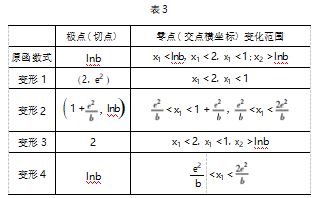
分别作函数f(x) 及其变形后各种函数的图形, 根据函数零点存在定理,借助图形的直观性,探究零 点位置变化规律.现将f(x) 及其变形后的各函数极 点(切点) 和零点变化范围归纳如下,见表 3:
不同的零点范围在对处理不同的问题时所产生 的效果也会不一样,“好”的函数容易发现函数零点 “好”的范围.联想目的是为了转化,因为一条信息 可能会联想到与此相关多条信息,因此在转化问题时,不能盲目选择化归方向,要盯住目标,以免走弯路,防止思路走入死胡同.正如波利亚所说 : 如果有 几条可能的途径,而其中没有一个是十分把握的,那 么,在沿着某一条路走得太远之前,最好对每一条都 稍加探索,不要过早地把自己局限于某一途径.
题目中式子结构“简与繁” ,条件与结论之间的 关系“明与暗” ,题型的“旧与新” ,都会直接影响看 题的效果,想问题的“浅与深”主导了解题的路向, 做题“粗与细”的习惯好坏决定解题的成败.在解题 的思维过程中,“看、想、做”心智动作紧密地联系在 一起,需要密切配合,协调作战.解题不仅能提高学 生的思维能力,培养学生分析问题、解决问题的能 力,还能培养坚忍不拔、锲而不舍的意志品质.在解 题教学中,教师不仅要还给学生思考问题的时空,做 到有机可思,更要让学生有法可究,增强学习力.
参考文献 :
[1]洪昌强.高考试题的“稳”与“活 ” ——— 以 2020 年和 2021 年浙江省高考压轴题为例[J].理科 考试研究,2022.29(19) : 25-27 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/69618.html