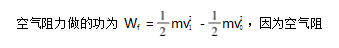SCI论文(www.lunwensci.com)
摘 要 : 在高中物理教学中,微元法是一种较为关键的解题法.在某些物理问题解析的过程中 能够起到化繁为简的作用,具有较强的应用价值.在文章阐述中以微元法为研究对象,旨在能够优化高中物理教学方法,为后续教学研究提供有效参考.
关键词 : 微元法,高中物理,解题
在涉及到变化物理量的研究中,我们通常是将全过程分为若干短暂小过程,或者是将整体分解为 微小的局部,亦或者是曲线看作是一小段一小段的 直线展开研究,进而归纳出适合全过程或整体的结 论.这种微小的过程或局部被称之为微元,这种方法 也被称之为微元法.目前在高中物理教学中,微元法较为常见,能够化抽象为具体.因此文章以微元法为 例,探讨高中物理解题教学中此种方法的具体应用策略.
1 微元法概述
在高中物理题目解析的过程中,微元法并不常用,但是起到的作用较大,其在运动类和电磁场类物 理问题解析的过程中,能够化繁为简,为学生提供解 题的技巧和思路.微元法中的“微”表示瞬间的物理 过程或短暂过程,“元”表示相对独立.微元法表示 从整体中选择一个微小过程,通过内外之间的联系 和规律来对整个物理过程进行了解和掌握.从数学的角度来分析微元法,即表示微元法类似于积分或者是极限过程,通过叠加即可以得出最终的结果和结论.一般来说,在微元法实际应用的过程中主要分 为以下几个步骤 : 首先确定研究对象 ; 其次选择微元 法 ; 再次借助物理规律对元的过程进行表达 ; 最后通过叠加求解得出最后的答案.
2 运动类物理解题教学中微元法的应用
运动类物理在高中物理教学中较为常见,包含 匀速、匀变速运动等等,如果采用常规思想和思维进 行解析,较为抽象.通过微元法的应用能够将抽象转 化为具体的问题,即在运动类物理问题解题的过程 中,选取微小的时间,确保在一定范围内不会出现较 大的变化,通过对路程或位移的求解得出最后的结 果.尽管对运动过程进行了分割,但是分割之后的各 个元之间仍然具有一定的规律性,因此在解析的过 程中只需要对相应的元过程叠加计算就能够解决物理问题,较为便捷.
例 1 水平的湖面上停着一艘船,船重记为 M, 船长记为 L,船员的重量为 m,现在船员站在船头的 位置,现接到指令,需要船员从船头走到船尾,在忽略船只阻力的情况下该船员从船头到船尾行走过程中船只的位移是多少?
解析 在本道物理题目解析的过程中,如果运 用运动学方法求解的难度较大,因此可以利用微元 法,配合整体思维,从而降低求解难度,解决物理问题.
解答 将船只与船员看作研究对象,根据题目 中忽略船员走动期间所受到的船只阻力,整体的系 统满足动量守恒的基本条件.在本道题目解析的过 程中对过程进行无限的分割,在较小的时间范围内 人的运动可以看作是匀速运动,船只和人在任意时 刻的速度可以将其记为 v1 和 v2 ,通过动量守恒定 律,从而得出 mv1 = Mv2 ,此时公式两边同乘 Δt,可得出 mv1Δt = Mv2Δt.因 Δt 较小,因此可以近似地将船只与船员的运 动看作是匀速运动,那么船只和船员位移大小则分别记为 Δs1 = v1Δt 和 Δs2 = v2Δt.
根据上述可知 mΔs1 = MΔs2 .通过对 上述划分的元位移进行叠加,可 知 mΣΔs1 = MΣΔs2 ,即 m s1 = Ms2 ,因 s1 和 s2 为船只和 船员在整个运动中的具体大小值,根据物理规律 L= s1 + s2 ,由此求出 s1 = mL/ (M + m) .
在位移问题解析的过程中,学生往往会被题目 的表象蒙蔽,从而找不到解题技巧陷入解题误区.如 果利用微元法解决位移问题,能够有效避免此种情况,使得题型变得简单便捷.
例 2 将一个物体竖直向上抛出,物体本身的 质量记为 m,抛出的速度记为 v0 ,已知该物体的运行速度与自身受到的空气阻力成正比,求 :
( 1) 在物体抛出到落地,空气阻力做了多少功,物体的瞬时加速度是多少?
(2) 物体在 t1 时间点的时候,高度是多少?
解析 根据题目中已知条件,可看出物体所做 的运动均为变速运动.物体在下落的时候速率为 v1 , 此时可以采用微元法来解决物理问题.
力为f = kv,物体下落最后的运动可以看作是匀速运 动,由此得出以 mg = kv1 ,在被抛出的时候物体产生了加速度,记为 a0 ,由此可知 ma0 = mg + kv0 .
(2) 物体在上升的过程中速度为 v,加速度为 a, 则- (mg + kv) = ma,则 a = -g-vg/v1.利用微元法 将物体在空中运动的过程划分为多个步骤,由此可 知 Δv = gΔt = -gΔt-vΔtg/v1 ,由此得出 0 -v0 = -gt - (g/v1 ) H,因此在 t1 时间点时,H = v1 v0 /g-v1 t.
在上述实例解析的过程中可以看出,微元法将 物体在运动中的过程看作是一个整体,并分解成多 个单元,通过拆解的方式帮助学生更好的理解,从而 使解题的过程也变得更加得简单和高效,久而久之学生便逐渐掌握了解题的技巧.
3 电磁场物理解题中微元法的应用
在高中物理教学的过程中,微元法不仅帮助学 生形成了较为便捷的解题技巧,还有效地拓展了学 生的知识视野,形成了较为清晰的解题思路.尤其是 面对高中物理教学中的电磁场问题,导体在实际运 动的过程中会受到安倍力作用,相应作用力大小也 会因此发生一定的改变,从而导致导体在磁场中运 动发生变化.在此类问题解析的过程中,不能直接应 用匀速或者是匀变速的物理规律对问题进行求解. 因此,在电磁场问题解析的过程中可以利用微元法, 将导体在电磁场中的运动进行无限的分割,并选取 其中较小的单元,将在此时间的运动看作是匀速运 动,借助物理的匀速或匀变速规律进行叠加计算,从而求解物理问题.
例 3 竖直平面中有一个正方形线框,电 阻 为 R , 质量为 m,边长为 L,平面 内包括垂直 向里 的磁场,线框 以 v0 的初速度水平抛 出,其方 向与 磁场方向始终保持垂直.已知磁场磁感应强度满 足 B = B0 + kz,Z 轴保持竖直 向下,重力加速度为g,求
( 1) 线框竖直方向速度为 v1 ,求其 中 瞬 时 电 流值?
(2) 复合场中运动期 间线框的最大电功率是多少?
(3) 线框从开始到瞬时速度为 v2 时候的耗时为 t,线框的总位移值是多少?
解析 在上述题目解析中,首先要考虑在电磁 场中导体的运动并非是均匀变化,因此不能利用匀 速或匀变速的物理规律进行求解.所以在本道题目 中采用微元法对题目进行分析,将导体运动的过程进行无限的分解,选取其中较小的微元进行求解.
解答 ( 1) 结合磁场中磁感强度的规律和正方向线框的规则特征,求出感应电流为 :
在上述案例解析的过程中,微元法的应用至关 重要.面对较为复杂的题型,微元法的应用不仅为学 生提供了解题思路,简化了解题的过程,并且在微元 法实际应用的过程中一定程度上拓展了学生的学科视野,为之后的学习做好了铺垫.
综上所述,在高中物理教学的过程中,微元法为 运动类和电场磁场类物理问题的解析提供了新的思 路和方向,能够化抽象为具体,应用的优势较为明 显.因此,在高中物理解题教学的过程中,教师要结 合例题的实际情况加强学生对微元法的认知,从而 帮助学生掌握微元法应用的解题技巧,促使学生的解题能力得到不断的提升.
参考文献 :
[1] 陈世福.高中物理解题中微元法的应用研究[J].数理化解题研究,2021 (25) : 81-82 .
[2]李衡斌.高中物理解题中微元法的应用[J].高 中数理化,2021 (16) : 30-31 .
[3]赖鹭传.高中物理解题中微元法的有效应用[J].数理化解题研究,2021 (19) : 81-82 .
[4]栾玉杰.妙用微元法,提升物理解题效率[J]. 高中数理化,2020(20) : 29 .
[5]郑成荣.“微元 法”在高中物理解题中的应用[J].中学物理教学参考,2020.49(12) : 75 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/69142.html