SCI论文(www.lunwensci.com)
摘 要: “说理”是学生借助分析、整合、表达来展现思考的过程和结果。有效的“说理”,便于学生增强数学 认知,发展思维能力。文章以课前、课中和课后三阶段为切入点,论述引导学生“说理”的策略,希望能使学生 获得良好发展,让数学课堂更精彩。
数学思维是数学学科的本质特征,亦是学生学习 数学的“工具”。数学思维串联起了从“四基”(基础 知识、基本技能、基本思想、基本活动经验) 到“四能” (发现问题的能力、提出问题的能力、分析问题的能力、 解决问题的能力)再到“三会”(会用数学的眼光观察 世界,会用数学的思维思考世界,会用数学的语言表 达世界)这一发展过程 [1]。基于此,一线教师、学者 总结出诸多切实可行的数学教学策略,“说理”策略是 其中之一。数学“说理”是指以各种数学情境为语境, 以 生活现象、数学活动、数学知识等为基础,借助语言 工具(符号语言、工具、图形语言、文字语言),发挥 理性思维作用,“说”思路,“说”方法,“说”思想,“说” 规则,“说”应用等,深入把握知识本质,发展思维能 力的活动。有效的数学“说理”,便于学生获得思维机 会,积极探究,不断地“说”,由此做到“三会”,增 强数学学习效果。
一、课前“说理”:设计学案,预习新知
课前是数学课堂教学的首要阶段。在此阶段,学 生要预习新知,做好课堂学习准备。学案能助力学生 预习新知。简言之,在学案任务的推动下,学生会理 清自主学习方向, 有针对性地学习新知, 建立良好认知。 同时, 学生会迁移新知认知, 解决学案中的练习题, 或 填写学案中的学习困惑, 借助“说”诊断自学情况, 明 确课堂学习要点, 增强课堂学习的针对性。基于此, 在 课前阶段,教师可设计学案,助力学生在预习新知中 “说理”。
以“平行四边形和梯形”为例,本节课的教学重 点之一是平行四边形的特征。围绕重点内容,教师可 设计如下学案(见表 1)。
在学案的助力下,学生积极思维,走进数学教材 中,探索平行四边形的特征。在自主探索后,学生迁 移已有认知,解决相关习题,“说”出预习问题。如此 学生便可心中有数地走进数学课堂,继续“说理”。
二、课中“说理”:多样活动,探究新知
(一)组织操作式“说理”活动
小学生的认知水平处于具体运算阶段,以形象思 维为主 [2]。在认知水平和形象思维的影响下,学生乐 于体验操作活动。在体验活动的过程中,学生会发挥 形象思维作用,分析数学现象,得出数学结论,建立 良好的数学认知。基于此,教师可以组织操作式“说 理”活动,让学生在操作过程中进行“说理”。
以“梯形的面积”为例,在本节课之前,学生探 究了正方形、长方形、平行四边形的面积公式推导过 程,积累了转化经验。教师依据学生学情,组织操作 式活动。在组织活动之前,教师提出要求:“请大家联 想推导正方形、长方形、平行四边形面积公式的过程, 归纳方法,试着动手操作,推导梯形的面积公式,并 当众描述推导过程及方法。”在这一要求的推动下,学 生积极思维, 回顾学习内容, 联想相关方法, 如转化法。 之后,学生纷纷发散思维,联想不同的方法,将梯形 转化为已知面积公式的平面图形。
在主动操作后,学生登台“说理”。如有学生将两 个完全一样的梯形模具拼成一个平行四边形。在操作 的同时,该学生逻辑清晰地表述:“梯形的上底 + 下底 的长度恰好是平行四边形的底边长。梯形的高和平行 四边形的高一样。所以,梯形的面积是平行四边形面 积的一半。平行四边形的面积公式是底 × 高。梯形的 面积公式则是(上底 + 下底)× 高 ÷2.”
学生通过体验操作式“说理”活动,不仅掌握了 数学知识, 还获取了数学思想与方法, 积累了活动经验。
(二)组织图像式“说理”活动
对于小学生而言,数学学习是从实物到图像再到 符号的过程。在此过程中, 学生会发挥形象思维作用, 剖 析图像,发现结论,建立数学认知,掌握数学思想与 方法。图像是数学“形”的具体表示,是学生认知“数”的 支撑。在课堂上, 教师可以组织图像式“说理”活动, 引 导学生与直观的图像互动,认真“说理”。
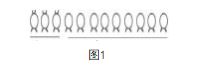
以“鸡兔同笼”为例, 在课堂上, 教师表达问题: “一个笼子里总共有 12 只鸡和兔子。这些鸡和兔子一 共有 30 条腿。请问,鸡和兔子各有多少只?”在学生 了解问题后,教师先指导他们使用列表法,探究鸡和 兔子的数量。接着,教师指导他们使用画图法。在指 导时,教师要求学生假设笼子里全是鸡。此时,大部 分学生发散思维, 想象画面, 认真作图, 直观分析, 理 清解题思路。之后,学生毛遂自荐,“说”思路。学生 代表展示图像(如图 1)并说道:“当笼子里全都是鸡的时候,一共有 24 条腿,少了 6 条。已知兔子有 4 条 腿。所以,少的 6 条腿,正是 3 只兔子的。所以,有 3 只兔子,9 只鸡。”
其他学生认真倾听,汲取经验。同时,学生因此 活跃思维,提出新的假设,如“假设笼子里全都是兔 子”,继而迁移已有认知,认真作图、解答、“说理”。
学生通过体验图像式“说理”活动,既轻松地解 决了数学问题,获得了多种问题解决方法,还掌握了 数形结合思想, 锻炼了数学表达能力和形象思维能力。
(三)组织符号式“说理”活动
数字、运算符号等是重要的数学语言。学生使用 数学表示文字、图像信息, 可以通过分析、比较、总结, 逐步得出数学结论,掌握数学知识,锻炼抽象思维能 力。基于此, 教师可以以数学文字、图像信息为重点, 组 织符号式“说理”活动。
以“商不变性质”为例,在课堂上,学生通过体 验多样活动,逐步了解了商不变的性质。于是,教师 要求学生用算式表示这一性质。在要求的驱动下,学 生进行逆向思维,根据“同时缩小”“同时扩大”“商 不变”这些关键信息,列出不同的算式。接着,学生 毛遂自荐,展示算式,认真“说理”。学生代表呈现如下两组算式(如图 2):
同时,学生还讲道:“第一组算式,除数和被除数 同时扩大 10 倍、100 倍、1000 倍, 商不变; 第二组算 式, 除数和被除数同时缩小 10 倍、100 倍、1000 倍, 商 不变。”在讲述的同时,学生代表重点强调了“同时缩 小或扩大相同的倍数”。其他学生认真观看、倾听,借 助数学算式理解商不变的性质。
学生通过体验符号式“说理”活动,不仅可以活 跃思维,将数学结论符号化,发展抽象思维能力,还 可以顺其自然地进行数学表达,提高数学表达水平。
(四)组织文字式“说理”活动
在学习数学的过程中,学生的数学词汇储备愈加 丰富。数学词汇是学生进行数学表达的基础。一般情况下,学生储备了丰富的数学词汇,就可以发挥思维 的作用,组织语言,表达自己对数学的理解。通过相 关表述,学生可以理清学习思路,获取学习方法,掌 握数学知识, 发展多样能力。对此, 在课堂教学中, 教 师可以依据学生的数学词汇储备情况, 组织文字式“说 理”活动,驱动学生迁移认知,积极表达。
以“圆的认识”为例, 在课堂上, 学生体验摸圆、 找圆、画圆、识圆、用圆活动,逐步了解了圆的基本特征。 基于此, 教师鼓励学生回顾五个活动, 联想圆的特征, 并进行描述。学生发散思维,记忆圆的不同特征。之 后,学生组织语言,描述圆的特征。学生代表说:“圆 是一个轴对称、中心对称图形。圆的对称轴是直径所 在的直线。圆中有无数条直径和半径。直径与直径、 半径与半径的长度永远相等。”其他学生有针对性地补 充,教师认真总结。
学生通过体验文字式“说理”活动,梳理、总结 了课堂学习内容,建立了完善的认知。
(五)组织应用式“说理”活动
学生学习数学是为了更好地体验生活,而解决数 学问题的过程正是学生“说理”的过程。学生可以“说” 思路、方法、应用等,增强对数学知识和问题解决的 认知,增强数学学习效果。鉴于此,教师可以依据学生 学情,紧抓现实生活,组织应用式“说理”活动。
以“长方体和正方体的表面积”为例, 在学生掌握 了长方体、正方体的表面积公式后, 教师可联系生活实 际,编创应用题,如“某品牌肥皂长 8 cm ,宽 5 cm, 高 4 cm 。为了提高销售量,超市准备将三块肥皂装在 一起进行销售。请你设计一下,怎样放这三块肥皂才 最节省包装纸,最少要使用多少包装纸?”在呈现应用 题后,教师给予学生充足的思考时间。
大部分学生能够积极思维,分析题目中的已知条 件和问题, 确定问题考查要点——最小表面积。之后, 学生在脑海中想象画面,按照不同的方式摆放三块肥 皂,画图并标注数据,计算长方体的表面积,继而选 出最小的表面积。在解决问题后,学生主动描述解决 问题的思路和方法。学生通过体验应用式“说理”活动,清晰地梳理 了解题思路,获取了解题方法,顺利地解决了问题。
三、课后“说理”:分层作业,应用新知
课后是数学课堂教学的拓展阶段,以数学应用为 主。学生的数学认知水平存在差异。在课后阶段,教 师要依据学生认知差异,分层设计作业,让每个学生 获得作业机会。同时,教师鼓励学生参与异质小组活动,合作“说理”,解决作业困难,实现“优带差,强 扶弱,对帮错”,提高学生的数学学习质量。
以“长方形和正方形的周长”为例,在课后阶段, 教 师以长方形和正方形的周长公式为重点,分层设计如 下作业:
在完成作业后,学生主动走进异质小组中。在小 组中,各组学困生“说”基础必做题的解决思路和方 法,中等生“说”巩固提升题的解题思路和方法,学 优生“说”拓展挑战题的解题思路和方法。在“说”的 过程中,其他组员认真倾听,发现问题,查漏补缺。
学生通过体验“说理”活动,不仅灵活地应用了 学习内容,还弥补了认知不足,丰富了解决问题的经 验,便于强化数学认知,提高解决问题的水平。
四、结束语
总而言之, 有效实施“说理”教学, 可以使学生在 “说理”的过程中,逐步增强数学认知,锻炼多种能 力, 获得良好发展。因此, 在组织数学教学的过程中, 教师要紧抓课前、课中和课后阶段,联系数学教学内 容,引导学生在课前预习中、在课堂活动中、在课后 作业中“说理”。在不断“说理”的过程中,学生会获 得多元发展,增强数学学习效果。
参考文献
[1] 康娘勉.基于深度学习的小学数学说理课堂的构 建[J].天津教育,2022(34):77-79.
[2] 许佰强.核心素养导向下构建小学数学说理课堂的 路径[J].亚太教育,2022(19):55-58.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/68923.html