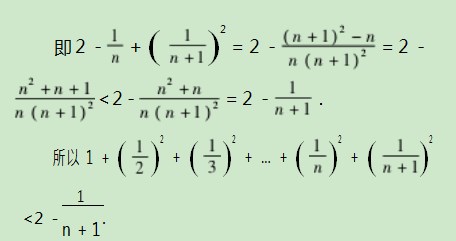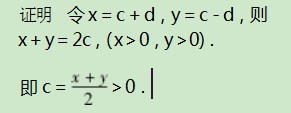SCI论文(www.lunwensci.com)
摘要:化归思想是高中数学教学中应用最广泛的一种思想.本文通过一些例题应用化归思想中的几种方法与原则对不等式进行证明.
关键词:化归思想;不等式证明;应用策略
不等式是基础数学中较为重要的内容,为高等数学的学习打基础,同时也是高考内容的重要考点.不等式的问题通常都会与其他章节的内容结合在一起进行考查,涵盖的内容知识量比较大.因此,在不等式的证明过程中,方法的运用比较灵活,可以通过方法的创新对不等式进行证明.在不等式的证明中采用化归思想的方法来解决问题就是一个很好的方法.将原始问题转化为新的较容易解决的问题,运用相应知识对新问题进行证明.最后将其还原到对原问题的证明.本文通过一些例题来探讨化归思想在不等式证明中的应用.
1化归思想的含义
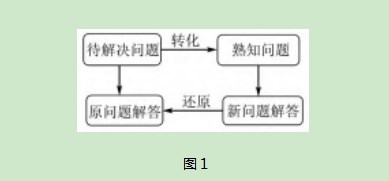
转化与化归思想是指将待解决的问题转化为熟知的问题,即化难为易、化繁为简,对新问题求解的一种数学思想方法.著名数学家罗莎通过对“化归法”的生动比喻,体现了化归思想的特点:将待解决的问题,经过转化,变为自己熟知的问题进行求解,最终回到原来问题的解决.这一解题过程可以用图1所示.
2化归思想的应用指导
2.1熟悉化归方法,能够灵活运用
在高中的数学解题中,教师经常让学生多做题,进行“题海战术”.通过大量的做题来提高解题效率,这种做法有一定的好处,但学生的思维得不到锻炼.化归方法有等价变形法、非等价变形法、引入参数法、换元法及待定系数法等一系列解题方法.学生在对不等式进行剖析的过程中,能够找到用化归思想中的一种方法进行解决.平常的教学中,教师要多对学生进行引导,锻炼学生的思维能力,对化归方法能够灵活运用,能够做到熟练掌握,且能够将问题有效转化.最终做到对不等式的有效证明.
2.2把握化归原则,进行简单转化
在高中阶段基础数学中,不等式证明的相关知识较为晦涩难懂,学生对于证明不等式的方法不够灵活,思维不够敏捷.在教学中,教师要向学生引入化归思想,引导学生把抽象的问题转化为形象具体的问题.学生能够理解简单化原则、熟悉化原则以及直观化原则,对于不等式的证明有更好的运用.将较难理解的问题转化为容易的问题,且能够用自己所熟知的知识对问题进行解决.对不等式进行简单转化,可以大大提高学生的解题效率.
3化归思想在不等式证明中的应用
分析观察发现,要证明的不等式直接证明有些困难.根据已知,能够联想到:sin2β+cos2β=1.即可以令a=xsinβ,b=xcosβ(x≤1).
证明令a=xcosβ,b=xsinβ,(x≤1),将a和b代入不等式左边,得
分析观察不等式,能够运用放缩法对不等式进行证明,使问题更简化.将左端从m=2开始逐步扩大,用归纳法对原式进行证明.
说明m=n+1时,该命题是真命题,即原不等式得证.
分析观察不等式左边是有关x和y的对称式,根据已知条件和不等式,可以运用三角代换进行证明.
证明因为x≤1,y≤1,令x=sinβ,y=cosθ,将sinβ和cosθ代入不等式的左端,得
分析已知条件为d+e+f+g=1,那么,能够取平均值为标准量,恰好使结果能够为1,可以引进参数α,β,γ,σ进行增量代换.
分析根据已知条件,要证x+y≤2会有困难,能够引入参数x和y做以变换,“x=c+d,y=c-d”可以使问题得到简化,方便于不等式的证明.
那么,x,c,y构成以c为等差中项的等差数列.
所以x3+y3=(x+y)[(x+y)2-3xy]=2.
即2c·(4c2-3xy)=2.即c·(4c2-3xy)=1.
分析观察不等式,不等式的右边为a+b+c,a+b+c,能够想到空间直角坐标系中,两点到原点距离的平方的表达式一样;不等式左边a1 a2+b1 b2+c1 c2可以看作空间中两个向量的内积,能够从这两者的联系着手对不等式进行证明.
证明设向量a=(a1,b1,c1),b=(a2,b2,c2),两向量的夹角为θ,
4结论
不等式是基础数学中极为重要的一部分,不等式的证明更是关键之处.证明不等式成立的方法有很多,诸如:柯西不等式法、基本不等式法、比较法、分析与综合法、换元法、放缩法、反证法、数学归纳法与几何法等.本文主要运用化归的思想对不等式进行证明,将原问题转化为熟知的、简单的以及容易解决的问题,最终还原到对原问题的解答.通过对几道例题的证明,从对于化归思想的原则上(熟悉化原则与简单化原则)及方法上(等价思想、不等价思想、对称代换思想、增量代换思想、和差代换思想与横向化归)的有效应用,使待证明的不等式转化为能够解决且熟悉的不等式,更有利于不等式的证明.不等式证明中,思想是灵魂,方法是关键.学生在运用化归思想证明不等式时,要能够熟练运用化归方法将问题有效转化,并能够掌握化归原则,对问题进行有效处理.
参考文献:
[1]彭乃霞,宋军.化归思想在递推数列中求通项的应用[J].数学通报,2011,50(07):49-51.
[2]官运和.数学方法论[M],北京:清华大学出版社,2020.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/66536.html