SCI论文(www.lunwensci.com)
摘 要 : 2022 年福州质检试题中的立体几何解答题有着难度低、得分易、入手宽、解法多、重基 础、显成效的特点,既能够很好地检验出高三学生经过一轮复习后立体几何问题的掌握情况,也能够体现教师的解题水平,是一道值得品鉴的问题.
1 问题呈现
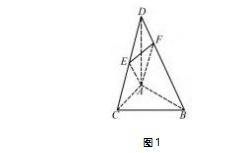
题目 ( 2022 年福州质检) 如图 1.在三棱锥 D-ABC 中,DA ⊥底面 ABC,AC = BC = DA = 1.AB =,E 是 CD 的中点,点 F 在 DB 上,且 EF⊥DB.
( 1) 证明 : DB⊥平面 AEF ;
( 2) 求二面角 A-DB -C 的大小.
2 命题意图
本题是一道立体几何的解答题,满分 12 分,其 中第( 1) 问 5 分,第(2) 问 7 分,具体考查如下 :
知识结构层面 : 考查空间中线面的位置关系、二面角的求法、向量方法在立体几何问题中的使用.
基本能力层面 : 考查推理论证能力、运算求解能 力与空间想象能力.
核心素养层面 : 考查直观想象、逻辑推理、数学 运算等核心素养.
数学思想层面 : 考查了数形结合、化归与转化、 函数与方程思想.
四翼评价层面 : 体现了“四翼”中的基础性与综 合性.
3 解法探究
3.1 第(1) 问解析
解法 1 因 为 DA ⊥ 平 面 ABC,且 BC ⊂ 平 面 ABC,所以 DA⊥BC.
因为 AC = BC = 1.AB =,所以 AC2 + BC2 = AB2.
所以 AC⊥BC.
因为 DA∩AC = A,DA,AC⊂平面 DAC, 所以 BC⊥平面 DAC.
因为 AE⊂平面 DAC,
4 教学启示
作为老师,应当积极归纳高考真题中的图形特 征,帮助学生培养空间想象能力.挑选常考的空间几 何体模型,让学生通过“眼观”,记住空间图形的结 构特征 ; 让学生通过“手绘”,增强空间想象能力 ; 最 后能通过“脑补”,在头脑中形成空间几何体.从某 种意义上来说,学生绘制的几何体的美观程度,在一 定层面上反映了该生空间想象能力的好坏.
注重基本定理的使用,关注问题求解的细节 ; 对 定理的记忆,必须做到“定理文字”“数学语言”“图 形表示”三管齐下 ; 对定理的应用,既必须“滴水不 漏”,也不能“画蛇添足”,如果教师能够解决证明过 程中的漏条件与添条件的问题,那么得分率的提高 将一马平川.
跳步易踩坑,踏实得满分,建系常规化,坐标逐 个求 ; 利用向量法求解坐标时,学生容易跳步走,特 别是对于中点、重心等点坐标,喜欢通过观察图形, 一步写出,这样的结果,对则全盘皆活,错则满盘皆 输,教师应当避免这样的情况发生,引导学生脚踏实 地,步步为营,特别是动点问题,对动点的坐标切不 可一步到位.
回归课本重基础,一题多变显神通.除了关注高 考的图形之外,课本也是很好的命题素材,事实上, 本题来自人教 A 版选修 2 -1 数学 P109 页例题 4 的 改编.
参考文献 :
[1] 中华人民共和国教育部.普通高中数学课程标准 (2017 年版 2020 年修订) [M].北京: 人民教育出版社,2020.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/66512.html