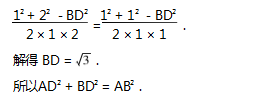SCI论文(www.lunwensci.com)
摘 要 : 对 2022 年高考数学甲卷立体几何学生答题情况的了解发现,很多同学第一问没找到 恰当的方法证明垂直,导致该题得分低或者未得分.现就本题第一问给出相应解法,从而归纳一些解题技巧.
关键词 : 平面几何,垂直,建系
1 原题呈现
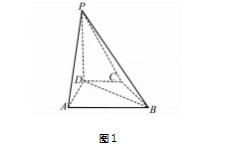
题目 ( 2022 年高考数学甲卷第 18 题第 ( 1 ) 问) 如图 1.已知四棱锥 P-ABCD 中,PD⊥平面 AB-CD,CD/AB,AD = CD = CB = 1.AB = 2.PD =根号2.证 明 : BD⊥PA.
2 试题解析
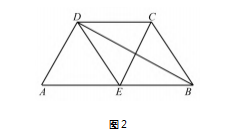
解法 1 如图 2.取 AB 中点 E,连接 DE,CE,DB.
因为 AB/CD,AB = 2.CD = 1.
所以 CD/BE 且 CD = BE.
所以四边形 DCBE 为平行四边形.
又 BC = BE = 1.
所以四边形 DCBE 为菱形.
所以 BD ⊥ CE.
同理可证 : 四边形 AECD 为平行四边形. 所以 AD/CE.
所以 BD⊥AD.
因为 PD⊥面 ABCD,所以 PD⊥BD. 因为 PD∩AD = D,PD,AD⊂面 PAD, 所以 BD⊥面 PAD.
因为 PA⊂平面 PAD,所以 BD⊥PA.
解法 2 由 AD = CD = BC = 1.AB /CD 知四边形 ABCD 为等腰梯形.
所以∠DAB + ∠DCB = 180°.
所以 cos∠DAB = -cos∠DCB.
在△ABD 和△CBD 中,由余弦定理知
解得 BD = 根号3.
所以AD2 + BD2 = AB2.
所以 BD⊥AD.
因为 PD⊥面 ABCD,所以 PD⊥BD.
因为 PD∩AD = D,PD,AD⊂面 PAD,
所以 BD⊥面 PAD.
因为 PA⊂平面 PAD,所以 BD⊥PA.
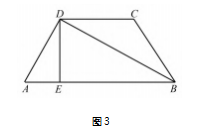
解法 3 如图 3.过点 D 作 DE⊥AB 交 AB 于点E,则在等腰梯形中,有 AE = 1/2.DE = 根号3/2.BE =3/2
所以BD2 = DE2 + EB2 = 3.
即 BD =根号3
因为 AD = 1.AB = 2.
所以AD2 + BD2 = AB2.
所以 BD⊥AD.
因为 PD⊥面 ABCD,所以 PD⊥BD.
因为 PD∩AD = D,PD,AD⊂面 PAD,
所以 BD⊥面 PAD.
因为 PA⊂平面 PAD,所以 BD⊥PA.
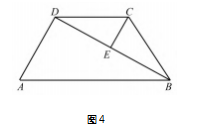
解法 4 如图 4.取 BD 中点 E,连接 CE. 在△BCD 中,CD = BC = 1.所以 CE⊥BD. 即∠DEC = 90°.
则在△DEC 与△BDA 中,
DE/BD=DC/BA=1/2
因为 AB/CD,所以∠EDC = ∠DBA.
所以△DEC∽△BDA.
所以∠BDA = ∠DEC = 90°.
所以 BD⊥AD.
因为 PD⊥面 ABCD,所以 PD⊥BD.
因为 PD∩AD = D,PD,AD⊂面 PAD, 所以 BD⊥面 PAD.
因为 PA⊂平面 PAD,所以 BD⊥PA.
解法 5 如图 5.取 AB 中点 E,连接 DE. 易知 CD/BE 且 CD = BE.
所以四边形 DCBE 为平行四边形.
所以 BC = DE = 1.
又 AD = AE = 1.所以△ADE 为正三角形. 即∠DAE = 60°.
在△DAB 中, 由余弦定理知
BD2 = 12 + 22 -2 × 1 × 2cos60°.
即 BD =根号3
因为 AD = 1.AB = 2.
所以AD2 + BD2 = AB2.
所以 BD⊥AD.
因为 PD⊥面 ABCD,所以 PD⊥BD. 因为 PD∩AD = D,PD,AD⊂面 PAD, 所以 BD⊥面 PAD.
因为 PA⊂平面 PAD,所以 BD⊥PA.
解法 6 由解法 5 知 DE = 1.
又 AB = 2.所以 DE = 1/2AB.
即 ED = EA = EB.
所以点 D 在以 E 为圆心,AB 为直径的圆上. 所以 BD⊥AD.
因为 PD⊥面 ABCD,所以 PD⊥BD. 因为 PD∩AD = D,PD,AD⊂面 PAD, 所以 BD⊥面 PAD.
因为 PA⊂平面 PAD,所以 BD⊥PA.
解法 7 由解法 5 知 △ADE,△DEC,△BEC 均 为正三角形.所以∠DCB = ∠DCE + ∠ECB = 120°.
在△CDB 中,由余弦定理知 BD =根号3
因为 AD = 1.AB = 2.所以AD2 + BD2 = AB2. 所以 BD⊥AD.
因为 PD⊥面 ABCD, 所以 PD⊥BD.
因为 PD∩AD = D,PD,AD⊂面 PAD,
所以 BD⊥面 PAD.
因为 PA⊂平面 PAD,所以 BD⊥PA.
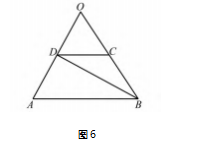
解法 8 如图 6.在底面四边形 ABCD 中,延长AD,BC 交于点 O,因为 AB /CD, CD =1/2AB,所以CD 为△OAB 的 中 位 线,即 C,D 分 别 为 OB,OA 中 点.又 OB = AB = 2. 所以 BD ⊥ OA.
即 BD⊥AD.
因为 PD⊥面 ABCD,所以 PD⊥BD.
因为 PD∩AD = D,PD,AD⊂面 PAD,
所以 BD⊥面 PAD.
因为 PA⊂平面 PAD,所以 BD⊥PA.
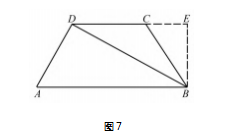
解法 9 如图 7.过点 B 作 DC 延长线的垂线,垂足为点 E,由解法 3 知 BE =根号3/2
又 BC = 1 ,所以 CE = 1/2
所以 DE = DC + CE =1/2
因为 PD⊥面 ABCD,所以 PD⊥BD.
因为 PD∩AD = D,PD,AD⊂面 PAD,
所以 BD⊥面 PAD.
因为 PA⊂平面 PAD,所以 BD⊥PA.
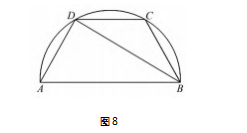
解法 10 如图 8.由 AB = 2.AD = CD = BC = 1. AB/CD,知四边形 ABCD 是以 1 为边长的正六边形 的一半.
所以 A,B,C,D 四点共圆,且以 AB 为直径. 所以 BD⊥AD.
因为 PD⊥面 ABCD, 所以 PD⊥BD. 因为 PD∩AD = D,PD,AD⊂面 PAD, 所以 BD⊥面 PAD.
因为 PA⊂平面 PAD,所以 BD⊥PA.
通过以上十种证明垂直的方法,涉及到的解题 方法有 : 勾股定理的逆定理、四点共圆问题、正余弦 定理、三角形的相似等,希望同学们从中可以受到启 发,对以后相关题目具有指引作用.
参考文献 :
[1] 徐胜林.2021 年全国高中数学联合竞赛加试(A卷) 平面几何题的证法赏析 [J].数 学通 讯, 2021 (22) : 56-59.
[2] 金磊,吕建恒.2021 年全国高中数学联赛平面 几何题 的几种证 法 [J]. 中学数学教学参考, 2021 (31) : 69-71.
[3] 赵 红梅.浅谈高中平面几何教学及实际应用 [J].数理化学习 (教研版) ,2019 (03) : 37-38.
[4] 冯艳妮.高中数学课程中平面解析几何内容设置的研究 [J].高考,2019 (05) : 139.
[5] 张晓兵.例说平面几何知识在高中数学中的应用 [J].高中数学教与学,2017 (17) : 13 -15.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/66466.html