SCI论文(www.lunwensci.com)
摘 要 : 通过平面向量基本定理推导笛卡尔平面直角坐标系下直线的截距式方程,结合仿射变 换中图象平行性与平直性不变的特点,将平面直角坐标系推广到仿射坐标系,推导出仿射坐标系下 直线的截距式方程,进而得到等和线的概念.
关键词 : 仿射坐标系,直线的截距式方程,等和线
在同一平面中相交于原点的两条数轴,如果它们的度量单位相等,称为笛卡尔坐标系,其中两条数轴互相垂直的笛卡尔坐标系,称为笛卡尔直角坐标系,否则称为笛卡尔斜角坐标系.笛卡尔平面直角坐标系是我们平时使用最多的坐标系.那么若两数轴 的度量单位不一定相等时就构成了平面仿射坐标 系.仿射变换是一种线性变换,能够保持图象的平行性与平直性,借助仿射变换这一特点,我们可以构建仿射坐标系.
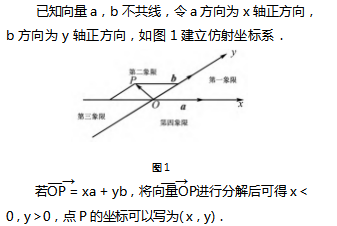
已知向量 a,b 不共线,令 a 方向为 x 轴正方向, b 方向为 y 轴正方向,如图1建立仿射坐标系.
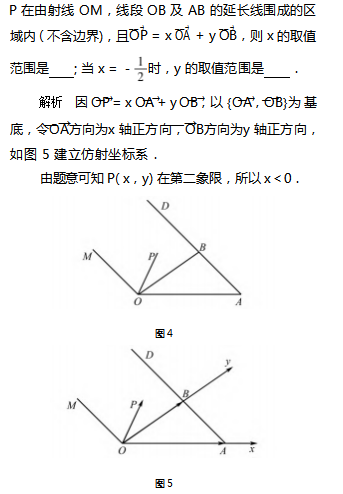
17 世纪初,笛卡尔建立了他的坐标系,这是变量数学的先导和基础,深刻地影响了数学的发展道 路.我们现在看来十分简单的笛卡尔坐标系,经过仿射变换成为仿射坐标系,借助平面向量基本定理的 推导让我们进一步地理解直线截距式方程就是等和 线的概念.向量是连接几何与代数的有效手段,通过 建系使点坐标化,进而几何的目标可以通过代数达 到,而代数的语言也可以用几何解释.
参考文献 :
[1] 苏凡文.研究高考题目,提高教研水平 [J].数学通讯,2014 (24) : 46-49.
[2] 代赵玉,许志城,魏俊潮.巧用等和线解决向量双变量问题 [J].数理化解题研究,2022 (25) :95-97.
[3] 钟建新.利用“等和线”解题 [J].数理化解题研究,2022 (04) : 67-68.
[4] 龙宇.利用“等和线”求解范围问题 [J].河北理科教学研究,2019 (04) : 4-6.
[5] 张玉虎.巧用向量等和线求解一类高考题 [J].数学教学通讯,2019 (12) : 84-85.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/66174.html