SCI论文(www.lunwensci.com)
摘 要
在“互联网+”环境下,结合适合的教学内容,采用翻转课堂教学模式,依照课前先学、课堂互动、课后延伸三个步骤, 通过制作微课视频、设计学习任务单、预设学生问题等方式构建课堂活动,激发学生主动参与、大胆发现探索的自主性,凸 显学生学习过程中的主体地位,促进初中学生学习自动力的提升。
学习自动力是一种自觉行为而非 自发行为,需通过适当的培养才可实 现。当前,互联网在全域范围内给教 育带来了前所未有的发展机遇和深刻 挑战, 日新月异的互联网环境是学生 需积极面对和主动适应的客观存在。 因此,我们应该在“互联网 +”环境 下,借助多元信息技术,实践好启发 式、探究式、讨论式、参与式教学, 激发学生主动参与、主动发现与探索的兴趣,促进学生学习自动力的提升, 让学生真正成为学习的主人。
一、着眼提升学生学习自动力的 课堂变革—教学模式的合理选择
教学有法,教无定法。没有一种 教学模式适合所有的教学内容,一种 教学模式必须与当前的教学内容、学 生学情乃至教师特征相契合。文章基于 苏科版教材数学八年级(上册)第 3 章 “勾股定理”第 1 节的内容展开探讨, 章节主要教学内容是探索勾股定理。
(一)先前活动经验支撑课堂探索 活动
学生在七年级学习整式乘法(单 项式乘单项式、单项式乘多项式、多项式乘多项式,乘法公式)时,通过 图形面积计算来获得数学猜想。本节 课也是借助图形面积的计算获得结论 的,因为有先前学习经验的迁移,大 部分学生可以通过观看微课视频进行 独立的尝试研究。当然,如果学生的 基础薄弱,可以在微课视频中回顾七 年级学习整式乘法时借助图形面积研 究问题的思路,唤醒学生的先前经验。
(二)勾股定理实践成就激发学生 探索热情
勾股定理揭示了直角三角形三边 之间的数量关系。在这之前,学生已 经了解了直角三角形内角的特点,也 知道作为一般三角形的三边关系(不 等关系),但不知直角三角形三边的确 定数量关系。通过对勾股定理的学习, 可以突破学生对直角三角形的初始认 识,激发学生的探究热情。当然,在 探索、发现勾股定理的过程中,计算 以斜边为边长的正方形面积时,学生 存在困难,为此,教师可以引导学生 采用多种方法尝试攻克这些困难,促 使学生主动而积极地参与探索活动, 促进学生学习自动力的提升。
综上所述,本节课采用翻转课堂的教学模式展开学习,可激发学生自 主学习、合作学习和探究学习的意愿, 促进学生学习自动力的提升。
二、搭建提升“学习自动力”的 平台—翻转课堂的教学实践
实施翻转课堂教学需要教师按照 课前先学、课堂互动、课后延伸三个 步骤展开,通过制作微课视频、设计 学习任务单、预设学生问题等方式来 组织课堂活动。
(一)课前先学:激发学习动力
客观而言,有些新知是可以通过 自学理解的,不需要传统教学中教师 的说教。“课前先学”便是让学生在学 习单的引导下,先自主进行学习。在 学习的过程中,遇见困难的问题时, 适时观看微视频,化解学习新知中的 难点。“课前先学”为学生提供了独立 思考的空间,促进学生主动学习,形 成良好的学习习惯,从而促进学生学 习自动力的提升。
1. 制作微课视频,引导学生“初学”
“初学”说起来容易,做起来不 易。探索新知的过程往往不是一帆风 顺的,需要充分的恒心及耐力。要让初中生静下心来攻克一个未知的问题, 其问题的趣味性弥足珍贵,这是让学 生保持好奇心和强烈的探究欲的根本。 因此,微课视频的设计应考虑:一是 视频中教学内容的呈现需要生动有趣, 例如,辅以生动活泼的动画音响等; 二是视频要预留给学生理解和解决问 题的空间,绝不能是平铺直叙,否则 有“灌输”之嫌;三是视频的内容既 要有知识的传授,更要有学习方法的 指导,真正体现助力学生自学的功能。
2. 设计学习任务单,引导学生 “深学”
将微课视频融入学习任务单中, 为学习赋予任务驱动,让本节课的学 习目标分解为具体的若干个小任务。 学生在学习任务单的引领下,有顺序、 有层次地展开深度学习,领悟“学什 么”“怎么学”“学得怎样”,让静态的 教科书变换为活跃的思考,充分凸显 知识的发生、发展过程。学生在此过 程中,不仅仅收获知识,更是多角度、 多方位发展能力。本节课的学习任务 单包含三个问题。
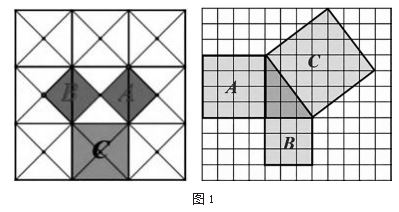
问题 1:相传 2500 多年前,毕达 哥拉斯从地砖图案中发现了直角三角 形三边之间的数量关系。现在,我们 也来观察一下这幅示意图(见图 1), 在此我把地砖的颜色给隐藏,让我们 可以清楚地发现图中每个小三角形都 是等腰直角三角形。假设每个小等腰直角三角形的面积为 1.图中三个正 方形 A 、B 、C 的面积分别是多少?三 个面积之间有什么等量关系?
问题 2:问题 1 中获得的结论是 在等腰直角三角形的前提下成立的, 那么,在一个任意的直角三角形当中, 这个结论是否还成立呢?
追问:如何求正方形 C 的面积呢?
问题 3:围绕“求正方形 C 的面 积”的讨论,你认为在方格纸上求一 个正方形的面积有哪些方法?请举例 说明。
(二)课堂互动:激活学习能力
“课堂互动”环节是将学生在“课 前先学”中获得的知识、活动感悟、 活动经验,在课堂中与教师和其他同 学进行交流、分享。这是学生对自己 之前的探索过程、结果的再次思考, 他将得到从其他同学或教师那里来的 不同思路、不同观点,当然,也包括 在先学阶段产生的疑问的释疑,这有 利于学生对获得的知识、技能及经验 的内化。与传统课堂相比,学生有更 多时间、更多机会与同伴和教师进行 交流。
1. 创设问题情境,激发探究欲望
建构主义认为:“知识的获得是学 习者在一定情境下通过人际协作活动 实现意义建构的过程。”为此,翻转课 堂要有与微视频内容相一致的教学资 源,并在适宜的问题情境下,将课堂互动持续而深入地推进。
实验:转动沙漏。要求学生认真 观察沙漏转动过程中的“变”与“不 变”(见图 2)。
问题 1:通过刚才的实验,你观 察到了什么?
问题 2:两个小正方形的面积之 和等于大正方形的面积。根据正方形 的面积计算公式,这个结论可以看成 直角三角形的两直角边的平方和等于 斜边的平方。那么,是不是所有的直 角三角形的三边都满足这样的数量关 系呢?
设计意图:用实验引入,激起学 生的兴趣,让学生在观察实验的过程 中,初步感受两个小沙漏的体积之和 等于下面大沙漏的体积;观察后进行 思考,如果忽略模型中厚度,可以得 到两个小正方形的面积之和等于大正 方形的面积,从而获得一个关于直角 三角形初步的结论:直角三角形的两 条直角边的平方和等于斜边的平方。
2. 设计探究问题,引发思维深入
“真正的学习活动在于把握和领悟 知识本身的意义,并能把它们转化为 自身的能量——智慧。”数学学习的真 谛在于思维的发展,而思维不是说出 来的,必须借助载体,而探究性问题 的解决是发展思维能力的关键。
探究 1:课本在探索“勾股定理”时,为何将直角三角形及三个正方形 置于方格纸上?除此之外,我们有没 有其他探索方法?
设计意图:让学生感受在方格纸 上探索勾股定理,其目的是便于学生 计算三个正方形的面积。又通过三个 正方形的面积关系去发现直角三角形 三边的数量关系。
探究 2:类似地,我们可否借助 探索“勾股定理”的方法,探究锐角 三角形和钝角三角形对应的三个正方 形的面积关系呢?
设计意图:既然直角三角形的三 边有那样的数量关系,那么类似地, 锐角三角形三边有怎样的数量关系 呢?我们依然可以通过三个正方形的 面积关系来发现锐角三角形的三边关 系,同样,对钝角三角形也是如此。
3. 规范探究程序,提高学习品质
课堂研讨需要更多学生参与,但 我们不能仅仅关注参与的广度,而是 要关注参与的深度,提升学生学习自 动力必须建立在参与有广度、有深度 的基础上,为此,在组织学生开展探 究活动时,需要强调两点。一是注重 指导学生的探究方法,探究前任务是 否明确,探究活动的要求是否明晰。 二是加强评价,采取灵活多样的评价 方式。教师的评价力求精准,不是笼 统地说“好”与“不好”,而要陈述 “好”的具体表现,以及“不好”的具 体表现,让学生心服口服。当然,也 可以将自我评价与同伴评价结合起来, 将结果评价与过程性评价结合起来, 充分发挥评价的激励功能。
(三)课后延伸:激扬学习个性
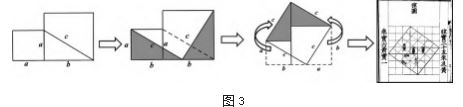
提升学习自动力不仅要训练学生 对学习内容认知的能力,更需要完善 学习态度、学习品质等具有个性化的 情感与思维特质。因此,在课后的延 伸阶段,可以给予学生更多空间,学生可以采用自己喜欢的方式研究感兴 趣的问题,教师无须加以限制。比如, 本节课课后,可以向学生介绍中国历 史上关于勾股定理证明的两颗璀璨明 珠(说明,图 3 和图 4 选自四川省成 都市石室中学邓燕老师的教学设计):
(1)赵爽弦图的证明思路(见图 3)
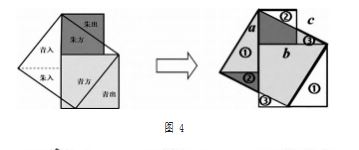
(2)东汉数学家刘徽的“青朱出 入图”的证明方法(见图 4)。
当然,要提升学生的学习自动力, 还需要将所学得的知识、方法、经验 迁移到新的情境实践中,内化为自身 的素质。也可以提出更为发散性的问 题,比如,基于以上两种证明方法提 出问题:“对比刚才呈现的三种证明方 法,如果我们从变换的角度看,思考 它们有什么共同特点? ”
三、结语
在互联网高速发展的今天,学习 自动力的培养迫切需要和网络技术进 行有效衔接,这对学生自主学习、创 新学习、终身学习能力的培养具有重要意义。因此,让学生顺应并借助 “互联网 +”的信息化时代,学会自主 学习,更好、更快地形成学习自动力。
参考文献:
[1] 何克抗 . 建构主义─革新传 统教学的理论基础 [J]. 电化教育研 究 ,1997(3):3-9.
[2] 李四海 . 化学课堂教学促进学 生可持续发展策略研究 [J]. 安庆师范学 院学报 ( 自然科学版 ),2005(4):125-127.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/65540.html