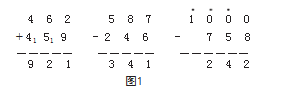SCI论文(www.lunwensci.com)
摘 要: 解题教学是小学数学教学的重要组成部分。目前小学生在解题时仍然存在解题过程混乱、结果不正确等 问题。文章基于小学数学解题教学案例,梳理了学生解题错误的原因,同时指出教师可以从基础教学、思维培养 教学、解题习惯培养教学三个角度出发开展解题教学工作,以期提高小学数学教学质量。
关键词: 小学数学,解题错误,归因,对策
引 言
在小学数学解题过程中,学生难免会因自身知识储备不够丰富、数学解题思维不够灵活等而出现错误。 此外, 一些学生会在相似的题目上重复犯错。为此, 小 学数学教师有必要探析学生解题错误的根本原因,同时基于根本原因采取相应的优化措施,从根本上解决学生 解题错误的问题。
一、小学生解题错误归因
(一)基础不牢固造成解题错误
目前在数学解题过程中,小学生存在错误地判断 问题考点、错误地应用数学概念、错误地套用数学公 式等问题,最终导致答题错误。究其原因,在于小学 生并未牢固掌握基础知识 [ 1] 。例如,在北师大版数学 四年级(上册)“除法”一课的习题教学中,有问题如 下:张老师带领 21 名学生游湖, 每条船能够坐 4 人,要 使学生全部坐上船,一共要租几条船?这一问题涉及 除法算理、有余数的除法算法等基本知识点。然而, 有 的学生基础知识不牢固,不能明确总人数与船载人数 之间的数量关系,无法列出正确的算式;有的学生由 于对算理、算法掌握不牢,在列出算式后计算时出现 错误答案。
(二)方法不灵活造成解题错误
小学数学内容丰富,题目形式变化多端 [2] 。小学生只有灵活应用不同的解题方法,才能够正确解决数 学问题。但是,部分学生在解题时存在惯性思维的问 题,如解题思路同质化,解题方法套路化等,不能以灵活的思维探究数学问题, 最终出现解题错误。例如, 在北师大版数学四年级(上册)“运算律”一课的习题 教学中, 有问题如下:用简便算法计算 98×32 的结果。 在解答这一问题时,很多学生将 98 拆分为 90+8. 将 32 拆分为 4×8.但仍然难以进行简便计算,反而增 加了计算量,容易造成计算错误。究其原因,在于这 一算式并未以符合乘法交换律、乘法结合律、乘法分 配律的一般形式出现。然而,部分学生习惯直接套用 a ×b ×c=a ×c ×b 、a ×(b+c ) =a ×b+a ×c 等公式解决 25×32×4、125×97×8 等形式规范的数学问题, 不能 对另外形式的问题进行拓展思考, 最终造成解题错误。
(三)做题不检查造成解题错误
小学阶段,不乏知识基础扎实、能力水平良好的 学生[3]。但这类学生在解决数学问题时仍然会出现错误。 例如,学生对三位数除以两位数的算理、算法掌握十 分扎实,且能灵活应用试商方法,但由于计算时代错 数值, 忘记退位, 最终导致解题错误。由此可以发现, 部分学生具备正确答题的能力,但由于自身马虎、不 认真而未能正确计算,也未能自我纠查出错误。
二、避免小学生数学解题错误的教学对策
(一)筑牢基础,扫除解题障碍
1. 趣味教学讲解知识,提升解题认知
数学知识具有一定的复杂性与抽象性。小学数学 教师应根据小学生的认知发展特征合理优化教学方 法,如采取情境、游戏等趣味教学方法,融入故事、 视频等趣味教学元素, 调动学生的理论学习积极性, 使学生在主动学习的过程中理解知识,进一步提升学 生的认知水平,为学生正确分析问题、解答问题奠定 基础。
例如, 在北师大版数学二年级(下册)“加与减”一 课的解题教学中, 为了让学生能够明确 462+459、587- 246、1000-758 等计算问题所考查的知识点,顺利运用 正确知识解决问题,教师需要先让学生理解三位数加 三位数(包括进位加)、三位数减两位数、三位数(包 括退位减)的算理与算法,帮助学生奠定解题基础。 但是,相关计算原理具有一定的抽象性,学生在计算 时容易忘记进位或退位,造成计算错误。要想让学生 快速理解相关知识,教师可以采取游戏教学法为学生 讲解计算原理。例如,教师可以在课内组织“卡片游 戏”:教师不断出示带有数学加减法问题的卡片,能快 速说出答案的学生晋级,剩余学生淘汰。之后,教师 依次出示 700-200、500+400 等几百加、减几百问题的 卡片,700-50、150-70、300-150 等几百几十加减几百 几十的问题卡片, 985-251、321+123、245-105 等几百 几十几加减几十或几百几十几的问题卡片,组织学生 快速抢答。此外,教师还可针对淘汰学生组织“复活 赛”,让他们翻阅教材、笔记,回想算理、算法,之后 再为他们出示相应题卡,正确解决题卡问题最多的学 生可以“复活”,继续参加比赛。所有学生均可在“卡 片游戏”中思考相关算理、算法, 巩固算数知识基础, 提高运算能力。完成游戏教学后,教师再对游戏结论 进行总结:三位数加(减) 三位数时, 要保证被减数、 减数相同数位对齐,不同位数分别相加减,并将得数 落在相应数位上,如果有进位则加 1.如果有退位则减 1.在此基础上, 教师再出题并引导学生应用具体算理、 算法解决问题(如图 1),有利于学生根据算理、算法 正确列出竖式并计算出问题答案。
2. 拓展教学,渗透数学思想,丰富解题内涵
将数学思想渗透进小学数学课程教学中,有利于 拓宽学生的数学学习视野,丰富学生的解题思路。在 完成基础知识教学后,教师可以围绕课程教学主题收 集、整理相应的数学思想教学内容,之后通过例题呈 现的方式为学生渗透数学思想, 指导学生在解答例题、 剖析例题的过程中感悟数学思想方法的奥妙,使学生 学会应用不同的数学思想与方法解决问题。
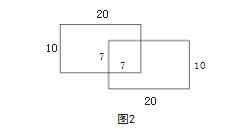
例如,在北师大版数学三年级(上册)“周长”一 课的解题教学中,有一个比较复杂问题的如下:图中不 规则图形是两个长方形组合在一起的,求这个图形的周 长。
这其实是一道非常规的求图形周长的问题。学生 多会按照普通方法求解问题,先求出不同部分线段的 长度,之后将不同部分线段长度相加,不仅计算步骤 烦琐,还容易在计算中出错。针对这一问题,在进行 解题教学时,教师可以先为学生渗透转化思想:转化 思想是化复杂为简单, 化含糊为明朗的一种数学思想。 在解决数学问题时,我们可以先观察题目特征,分析 题目中的问题是否可以转化为更加直观、更加明朗的 问题,之后用更加简单的方法解决问题。
说明转化思想的内涵后,教师可以指导学生应用 转化思想解决此数学问题:“根据转化思想,我们可 以使用移补的方法将复杂的不规则图形转化为标准图 形,如三角形、正方形、平行四边形、长方形等。根 据原题内容,我们可以应用转化思想将组合图形移补 成新的标准图形——长方形。此长方形的长为 20+20-7=33. 宽为 10+10-7=13.之后,我们可以使用求图形 周长的计算公式求得移补后标准图形的周长:(33+13) ×2=92.”
这样,教师通过拓展教学,渗透转化思想,可以 让学生掌握化复杂为简单的解题方法,从而提高学生 的解题效率。
(二)活跃思维,提升正确解题能力
机械套用数学公式、数学模型是导致学生错误解 题的主要原因之一。学生之所以机械套用数学公式, 是 因为未能理解数学公式本质。为此,教师可以在小学 数学教学中组织专项习题练习,通过一题多变、一题 多解练习,加深学生对类型问题的理解,使学生明确 数学公式、数学模型本质,掌握合理分析问题及合理 应用数学公式、数学模型的要领,从而提升学生解题 能力。
1. 在练习中组织一题多变活动,提升分析能力
在小学数学解题教学中组织一题多变教学活动, 可 以让学生有更多迁移练习的机会,从而提升学生的数学分析、数学迁移、数学应用等能力。在具体练习中, 教师可以先围绕课程教学主题搜罗典型例题,之后围 绕典型例题设计变式问题, 组织学生在课上解答题组。
例如,在北师大版数学五年级(上册)“多边形的 面积”一课的解题教学中,针对本课教学内容,教师 可以搜罗以下应用例题。
例题:有一批圆木堆成梯形, 最上面一层有 3根,最 下面一层有 8 根,相邻两层相差 1 根,一共堆了 6 层,这 堆圆木共有多少根?
根据例题给出的信息,可以将求圆木根数的问题 转化为求梯形面积的问题, 之后套用计算公式 S梯形=(上 底 + 下底) × 高 ÷2 进行解答,得到这堆圆木共有 33 根的答案。
为了让学生进一步理解此类问题的内涵,教师还 可以设计类似问题,供学生分析、思考、探究。
变式 1:一堆钢管, 最上层 5 根, 最下层 10 根, 每 相邻两层差 1根,一共有6 层,这堆钢管一共有多少根?
变式 2:一堆钢管, 最上层 1 根, 最下层 11 根, 每 相邻两层差2根,一共有6 层,这堆钢管一共有多少根?
变式 1 仍可看作求梯形面积的问题,变式 2 可以 看做求三角形面积的问题,可以分别应用面积求解公 式 S 梯形 = (上底 + 下底) × 高 ÷2 与 S 三角形 = 底 × 高 ÷2 解决问题。完成变式问题教学后,教师可以让学生 讨论不同问题的解题过程,让学生在讨论过程中进一 步锻炼问题分析能力。
2. 在练习中落实一题多解,发展多元思维能力
在实际教学中,教师可以分析本课教学内容与其 他课程教学内容的关联,之后综合不同知识点的关联 设计解题方法多样化的数学问题。教师可以组织学生 应用不同的方法解决问题,并鼓励学生分享不同解 法,使学生在思考、运算、分享的过程中认识到数学 解题方法的不唯一性,从而发展多元解题思维能力。
例如,在北师大版数学六年级(上册)“比的认 识”一课的解题教学中, 教师可以综合本课教学内容、 过去教学内容设计问题:如果有 140 个橘子, 按照 3 ∶ 2 分应当怎样分?之后,组织学生以小组为单位讨论问 题,让学生通过讨论发展多元解题思维能力。
生 1:可以先将橘子平均分成 5 份,之后按照比 例相乘,算出不同部分橘子数量,具体计算过程如 下:140÷(3+2) = 28(个),28×3 = 84(个),28×2 = 56(个)。
生 2:可以先将橘子平均分成 5 份,之后先计算出“3”比例份额的橘子数量, 之后用总数量减去“3” 比例份额的橘子数量, 得到“2”比例份额橘子数量, 具 体计算过程如下:3+2 = 5. 140÷5 = 28(个),28×3 = 84(个),140-84=56(个)。
生 3:可以将比例问题转化为分数乘法问题,具体计算过程如下:3+2 = 5.140×3/5=84(个),140×3/5=56(个)。
这样,教师先通过呈现具体问题激活学生的解题 思维,之后组织学生围绕问题展开讨论,能使学生在 思考问题、分析问题、讨论解法的过程中学会综合应 用加、减、乘、除等多种方法解决问题,形成多元解 题思维能力。
(三)培养习惯,培养纠错改正素养
教师应以平常心看待学生的解题错误,并采取恰 当的方法培养学生纠错、集错的学习习惯,以此发挥 “错误”的育人价值,避免学生再次犯相同的错误。 为此,教师应在小学数学解题教学中积极组织习题检 查活动、习题纠错活动等教学活动。在活动中规范学 生的解题行为,逐渐培养学生自我查错、自我纠错、 自我改错的习惯,提升学生的正确解题素养。
结 语
综上所述,造成小学生数学解题错误频频的根本 原因主要在于学生对基础知识的掌握不够充分、解题 思维不够灵活、未养成检查的习惯。教师只有明确学 生的根本错误原因,并基于此采取针对性的教学对 策,才能有效矫正学生错误的思维习惯, 提高学生审题、 解题的准确率。为此,教师应不断提升自身专业教学 素养,坚持问题导向,明确学生的根本错误原因,同 时针对学生的错误原因采取有效的教学对策,弥补学生 的学习漏洞,矫正学生错误的解题思维习惯,培养学生 分析问题、解决问题的能力,提高小学数学教学质量。
[参考文献]
[1] 吴杨.小学数学高年级问题错因及矫正措施思考[J].小学生,2022(12):49-51.
[2] 缪莉莉.以“错”为师 以正认知:小学数学课堂中 的错题转化对策[J].教育界,2022(21):56-58.
[3] 刘红红 .小学高年级数学系统化错题教学环节分布策略[J].读写算,2022(31):111-113.
作者简介:黄美珠(1978.12-),女, 福建南安人, 任教于南安市梅山中心小学,一级教师,本科学历。
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/65181.html