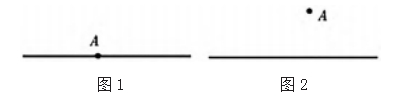SCI论文(www.lunwensci.com):
摘 要
“直线、射线、线段”在教学中需要构建教学主线,梳理重点内容,解读教学价值。实践探究建议从直线认知、概念辨析、 语言转化三部分开展教学探究,引导学生探索新知,总结归纳。本文将围绕“直线、射线、线段”的知识重点开展教学探讨。
[关键词] 直线 射线 线段 公理 概念
“直线、射线、线段”是初中几何学习的起始内容,是 最为基本的几何图形,是后续图形探究的基础,也是重要 工具。教学中需要合理设计环节,使学生掌握对应知识, 发展学生的空间几何观,培养学生的推理能力,下面开展教学探讨。
一、构建主线,明晰教学重点
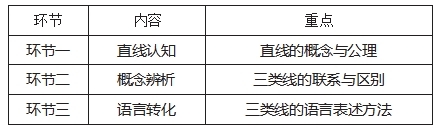
“直线、射线、线段”属于几何概念教学, 该章节内容 的教学方式可为后续几何图形的学习提供参考。教学中要充分解读教材,合理重构,围绕知识重点构建教学主线。 对于“直线、射线、线段”的教学主线,可以解读为“直 线认知 →概念辨析 →语言转化”。
针对上述主线,可分三个环节开展教学。其中:环节 一为直线认知,引导学生掌握直线的表示方法;环节二为 概念辨析,引导学生发现直线、射线、线段的区别与联系; 环节三为语言转化, 引导学生巩固直线、射线、线段的表 示方法,掌握数学语言。
而关于章节内容的教学价值,可以解读为四方面内容: 一是基于教学主线,按照“模型— 图形— 文字—符号”来 深入探究对应的知识概念;二是从几何图形的形状、大小、 位置关系三部分入手进行探究,掌握几何的研究方法;三是学习几何语言,掌握几何图形的规范表示;四是探究过程积累经验,培养逻辑思维,促进综合素养的提升。
基于上述主线研究与教学价值解读, 实际教学中建议 采用探究发现与归纳总结的方式。引导学生参与探究活动, 在实践操作中发现问题、提出猜想、验证猜想、归纳结论, 完成知识的探究总结与能力提升。
二、探究实践,掌握直线公理
“直线”是基本的几何图形之一,该环节的教学重点有两点: 一是直线的公理, 二是直线的表示方法。对于“直线公理”这一事实,学生不太熟悉,主要体现在两方面: 一是经过两点有一条直线的“存在性”,二是经过两点只有 一条直线的“唯一性”。教学中建议采用自主操作、实践探 究的方式,引导学生得出直线的公理,深刻理解公理中所隐含的存在性和唯一性。而直线表示方法教学中,建议借助直观多样的图像,开展辨析思考。
(一)“一点”出发,引出概念
实际教学可按照“生活举例 → 实践操作 → 启发思考” 的方式设计探究活动,引导学生思考。
生活思考: 如果要将准备好的木条固定在墙面上,至 少需要几枚钉子?
操作活动: 在平面内有一点 A, 请在该平面内画一条直 线 l。
启发思考: 所画直线与点是怎样的位置关系? 有几种 情形?
引导学生操作实践,呈现两种位置情形,即图 1 中直 线过点 A,图 2 中点 A 在直线上。在此基础上开展进一步 引导,让学生过点 A 再画一条直线 m ,让学生思考直线 l 与 m 的位置关系,引导学生感知两条直线的相交关系,以 及直线相交的概念,重点教学“交点”概念。
(二)“两点”探究,公理生成
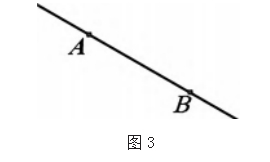
经过上述探究, 学生已经了解到过平面内的一点可以 画无数条直线,在此基础上进一步引导学生探究思考:过平面内的两点,可以画几条直线?
教学中设定两点 A 和 B,让学生过两点绘制直线(如 图 3),小组讨论,从而得出结论:过两点只可以绘制一条 直线。教学时需要从“存在性”和“唯一性”视角开展辨 析,引导学生思考是否还有其他的直线,并生成公理 — 经过两点有一条直线,并且只有一条直线,即两点确定一 条直线。关于该定理, 引导学生深刻理解其中的“有”所 表述的存在性,“只有”所隐含的唯一性。
(三)直观呈现,辨析表示方法
上述活动中学生已经绘制了多条直线, 该环节可将直 线组合在同一图像中,从辨析区分角度来探索直线的表示 方式。
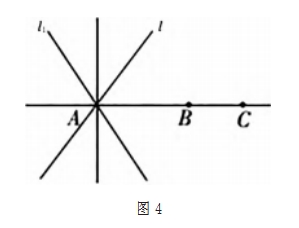
如图 4 所示,如何来表示经过 A 、B 、C 三点的这条 直线?
设问 1 :怎样用大写字母来表示直线?是否还有其他 的方法?
设问 2 :直线 AB 和直线 BA 是否表示同一条直线,若 表示同一条直线,是否可以将字母的顺序调换?
教学中引导学生探索直线的表示方式,形成三种方法: 一用两个大写字母(如 AB);二用一个小写字母(如 l); 三是字母与数学的组合(如 l1 )。同时引导学生辨析对于过 多点的直线,其表示方法是否一致,是否会出现混淆。
三、对比认知,发现联系区别
直线、射线与线段是相近的概念,学生很容易混淆 三者,在完成直线教学后,可以从知识生长视角开展进 一步探索,生成射线与线段的概念。再从端点个数与延 伸情况两方面来进行联系与区别的辨析。
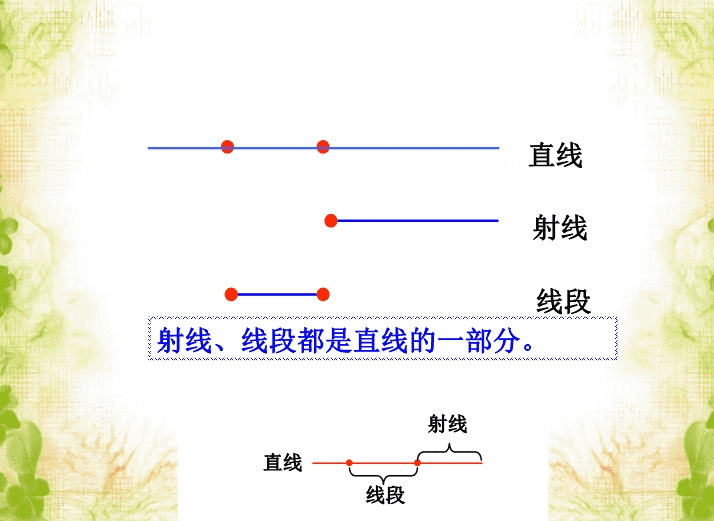
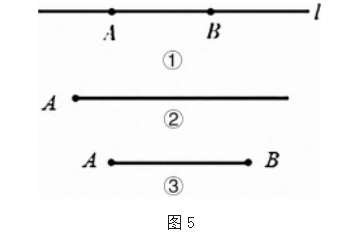
实际教学以直线为射线与线段的概念生长点, 呈现如 图 5 所示的直线 AB,进行衍生设问。
设问 1 :若将直线上点 A 的左侧擦去,如图 5- ②, 则 该线还是直线吗?
设问 2 :若再将线上点 B 的右侧也擦去,如图 5- ③, 则该线又是什么?
教学中通过直观的图形来给出射线与线段的概念, 同 时引导学生关注图形中三线的特征, 从端点视角进行总结。 而对于延伸性的辨析,则可以从长度测量视角加以解读。
活动设计:呈现图 6 所示的图形,让学生思考其中有 哪些直线、射线和线段。
设问 1 :请表示图中的线段、射线和直线。
设问 2 :对于直线 AB,是否可以测量其长度?射线 AO 和AB 呢?
设问 3 :线段 AB 和 AO 的长度又是否可以测量?
教学中基于图形开展延伸性探讨, 从长度测量视角进行分析, 学生可以直观地得出结论。关于直线、射线、线段的联系与区别探讨,可以引导学生进行列表对比,即让 学生按照下表进行知识梳理,掌握三线的表示方式,关注三线的延伸性、端点个数、长度是否可以测量,形成完整 的知识体系。
四、语言转化,提升综合能力
几何是一种特殊的语言,章节中的直线、射线、线段 同样是一种几何图形,三线的表述是教学的重点,这就要 求教师在实际教学中合理设计环节,灵活实现图形与语句 之间的转化。探究训练建议结合具体情形,关注其中的位 置关系和线的表示方法。
本章节中需要引导学生掌握点与直线的位置关系,以及 两直线的相交关系表示。教学引导建议采用语言互化表述的方式, 即完成“直观图形”与“语言描述”的对应转化。
(一)描述图形关系
以点在直线上和两线相交为例,教学呈现如图 7 所示 的图形,引导学生思考。
设问 1 :图 7 的①和②中分别含有哪些几何图形?
设问 2 :如何描述图①中点 P 和 l 的位置关系?
设问 3 :图②中的直线 m 和 n 是什么位置关系?如何 来描述?
教学中引导学生按照“图形确认 → 关系确定 →语言描 述”的思路来加以分析。以图①为例,图形为直线 l 与点 P → 两者为重合关系 → 点 P 在直线 l 上,或直线l 经过点 P。显然同理图②中有直线 m 、直线 n 和点 O →两者相交 → 直线 m 与直线 n 相交于点 O。
(二)作图呈现关系
而对于图形关系的表述还可以采用读题绘图的方式来引导,即引导学生根据语言描述来绘制图像,该方式可视为对图形关系的直观呈现。
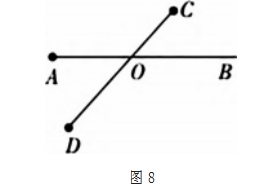
教学中可分步描述, 引导学生作图, 以两线的相交关系为例,如图 8。
请根据如下描述作图:①在平面内取两点 A 和 B ;②作出线段 AB ;③在线段 AB 上取一点 O ;④作线段 CD,使 线段 CD 与线段 AB 相交于点 O。
上述根据语言描述作图, 隐含了两大内容: 一是文字 语言与图形之间的转化关系;二是作图的逻辑顺序,尤其是两线相交的做法。教学中要注意引导学生提取文字中的 关键词,根据位置关系作图操作。同时语言与图形的转化 过程中隐含了数形结合方法,教学中要引导学生思考,体 验转化过程,提升学生的素养。
总之,“直线、射线、线段”是几何部分的基础知识, 其中的知识与技能是后续几何探究的基础。教学中建议采 用启发式、发现式、直观的教学方法,将重心转移到学生 的探究体验上,引导学生操作实践、猜想总结,深刻领悟 直线公理,掌握表示方法,能够灵活进行转化语言,让学 生在知识探索中获得能力的提升。
参考文献:
[1] 章静静 . 展开想象,感悟特征 — “直的线—射 线和直线”教学设计与意图 [J]. 数学教学通讯,2020(4) : 24-25.
[2] 吉裕艳 . 例谈同课异构的互慧价值— 以“直线、射 线、线段”同课异构为例 [J]. 中学数学, 2020(8) :5-6+10.
[3] 孙洁 . 基于“同质课”的小初衔接教学实践与思 考 — 以“线段、射线、直线”为例 [J]. 中学数学教学参 考, 2021(20) :61-63.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/63751.html