SCI论文(www.lunwensci.com)
摘 要: 数形结合是研究数学问题的基本方法,它包含“以形助数”与“以数辅形”两个方面.几 何画板把代数的精确刻画与几何图象相结合,为数学学习提供一种新的学习环境,使数学思维形象 化,使学习者亲历数学知识的形成以及探索规律的过程.
关键词: 几何画板,数学思想,深度学习
问题 1 如图 1.四边形 ABCD 是边长为 4 的正 方形,一个动点 P 从点 A 出发,沿着边 AB→BC→ CD →DA 运动,返回点 A 后停止运动,设点 P 走过的路 程为 x,将线段 AP 的长表示成x 的函数f( x).
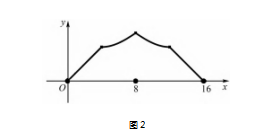
这是 2019 年湘教版必修第一册习题 3.1 的 15 题的第一 问.得到 f( x) 表达式后,可以知道函数的 定义域、值域、单调性,还有什么特性? 一时不知道. 利用几何画板作出函数图象,如图 2.图象类似钢笔 的笔头,我们称为“笔头线”.图象的对称轴为直 线 x = 8.我们再回到问题情境,通过思考点 P 的 运动,线段 AP 长度的变化情况,也可得出图象的 对称轴. 由函数的图象归纳性质是研究函数的一 种方法,但 不 能 只 依 赖 图 象 归 纳 性 质,因 部 分 图 象得出结论未必可信,所以要提高利用函数解析 式获得性质的能力.
问题 1 可以得到如下变式:
如图 3.正五边形的边长为 1.一 个动点 P 从 点 A 出发,沿着边 AB→BC→ CD→ DE→ EA 运动, 返回点 A 后停止运动,设点 P 走过的路程为 x,将线段 AP 的长表示成 x 的函数 f( x).
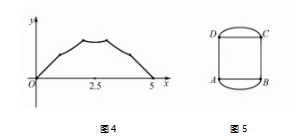
由问题 1 的解题经验,可以根据题意得出图象 的对称轴是 x = 2.5.但函数的图象还不太明了,利 用几何画板可以作出来,如图 4.
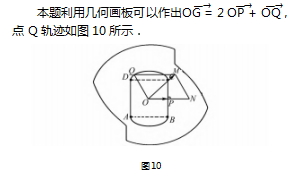
问题 2 如图 5.O 为边长为 2 的正方形的中 心,以 O 为圆心的两段圆弧 AB,圆弧 CD 与线段 AD,BC 组 成 一 个 环 道,P,Q 是 环 道 上 两 个 点,
本题 是 网 上 一 道 流 行 的 题 目,也 出 现 过 错解.本文提 供 详 细 的 解 答,但 是 要 弄 清 本 题 的 本
几何画板可以将一些抽象问题具象化呈现出 来,使我们更加直观地了解问题本质; 几何画板,让 思维的过程可视化,探究的过程不断深入,我们在不 断动手动脑、学思结合、数形互补中,思维能力得到了深度发展.
参考文献:
[1] 郑毓信.数学深度教学的理论与实践 [M].南京: 南京凤凰教育出版社,2020: 10.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/63134.html