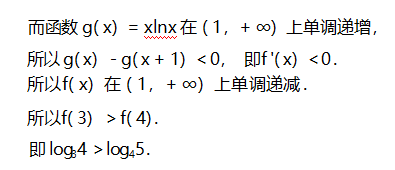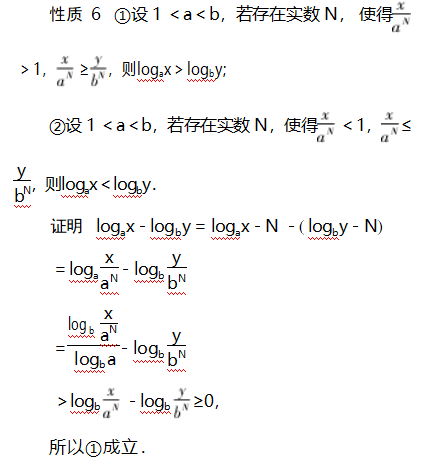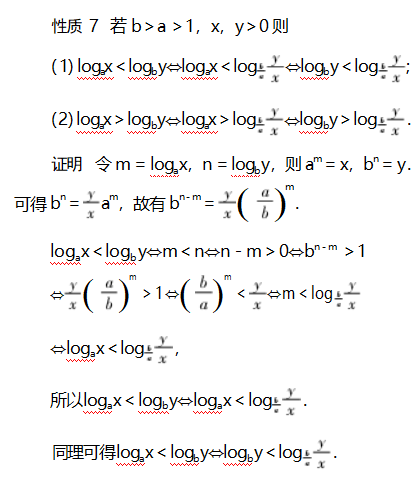SCI论文(www.lunwensci.com)
摘要:不同底数不同真数的对数比较大小问题,有没有规律可循?通过利用教材课后习题,挖掘隐藏在其背后的解题方法、数学思想,从特殊命题拓展出一般性的命题,顺利解决了对数比较大小问题,学生在活动过程中培养了四基四能,发展学生数学运算、逻辑推理等核心素养.
关键词:对数,比较大小,数学运算,核心素养
对数比较大小问题是每年高考的热点题型,题型杂方法多,重点考查数形结合思想、化归转化思想,以及数学抽象、数学运算、直观想象等核心素养,那么对于底数不同、真数也不同的对数比较大小,究竟要应用什么方法予以解决呢?本文以人教A版必修第一册一道习题为例对该问题进行探究.
1试题呈现
2解法探究
评析通过构造函数,研究函数的单调性,利用单调性比较大小,也是我们常用的一种策略,解题教学中要给予充分的关注.
3解题反思
本题中两个对数的底数和真数具有规律性,我们可以将它推广到一般性结论.
4高考真题链接
比较大小问题是经典的题型,教材中蕴含有多种解题方法,如作差法、构造法、单调性法、基本不等式法、不等式性质法、分析法、中间量法、图象法等,充分挖掘教材中的解题方法,通过一题多解教学,培养学生的数学运算能力,促进数学思维的发展,培养学生发散思维能力,同时也让学生进一步体会到不同知识之间的紧密联系.通过对习题的拓展,学生依据从特殊到一般的推理,从特殊的命题log3 4>log4 5出发,得到一般性的命题:若b>a>1,n>0,m≥1,则有logam+n(bm+n)<loga b,从具有规律的底数、真数关系的对数比较大小问题,归纳出了一般性的不同底数、不同真数的对数比较大小性质6、性质7,在活动过程中,提高了学生发现问题、提出问题的能力,培养和发展了数学抽象、逻辑推理、数学运算等核心素养.
参考文献:
[1]中华人民共和国教育部.普通高中数学课程标准(2020年修订版)[M].北京:人民教育出版社,2020.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/60980.html