SCI论文(www.lunwensci.com)
摘 要
本文赏析特级教师朱国荣的“圆柱的解决问题”一课。朱老师借助圆柱形体,让学生感悟“倒过来”的转化;借助斜截圆柱, 让学生感悟“倍拼”的转化;借助三角形面积,让学生感悟“添补”的转化。
[ 关键词 ] 圆柱问题,转化思想,教学赏析
素养导向和能力立意的数学课堂不仅要关注基础知识 和基本技能的教学,更要关注基本思想和基本活动经验, 发展学生的“四能”和“三会”。本文赏析了朱国荣的“圆 柱的解决问题”一课,他借助生活情境特级教师,让学生 提出问题并体会“倒过来”的转化;借助计算斜截圆柱的 体积,让学生想到“倍拼”的转化;借助计算三角形的面 积,让学生感悟“添补”的转化。整节数学课,从一个问 题引出一类问题,让学生在知识的前后联系中感悟转化思 想的应用。
【教学片段】
片段一:借助圆柱形体,感悟“倒过来”的转化
1. 借助生活情境,提出数学问题
师: 今天朱老师带了一瓶水,原来水是满的。现在有 点渴了,我要喝几口。看了这个情境后,你觉得可以解决 哪些数学问题?
(有的学生说“还剩多少水”,有的学生说“喝了多少 水”,有的学生说“一共多少水”。)
师: 你觉得在这三个问题中哪个问题最容易解决?
生 1: 一共有多少水。
生 2: 还剩多少水容易解决。一共多少水和喝了多少 水,上面是一个有点像圆锥的不规则图形,不好算。
师: 如果要求还剩多少水,要知道什么?
生: 要知道这个水杯的底面直径和现在水的高度。
2. “倒过来”转化,计算不规则图形
师: 要求一共多少水,朱老师喝了多少水是个关键问 题,谁有想法?
(有的学生说:“先做一个记号,把水给灌满,再把水倒进一个规则的容器里或者量杯里,就能算出来”;有的学 生说:“不规则图形我们是算不了的,所以我们把它倒过 来。下面就是一个圆柱体,我们知道圆柱体体积怎么求, 所以就可以算出喝了多少水。”)
师: 当我们遇到不规则图形的时候,可以把它转化为 规则图形。(教师实物演示。)你怎么知道它们的形状变了, 体积是不变的?
生: 这个瓶子总体积是不变的,剩下的水也是不变的, 所以倒过来之后喝了的水也是不变的。
师: 用一个巧妙的办法把不规则图形转化为规则的圆 柱体了。(出示题目:一瓶装满的矿泉水,朱老师喝了一 些,把瓶盖拧紧后倒置放平,无水部分高 10 厘米,内直径 是 6 厘米。朱老师喝了多少水?) 同学们,列式计算并写上 答案。
生: π 乘 6/2 的平方等于 9π,再乘 10 等于 90π 立 方厘米,90π 立方厘米等于 90π 毫升。
师: (出示题目:一个内直径是 8 厘米的瓶子里,水的 高度是 7 厘米,把瓶盖拧紧倒置放平,无水部分是圆柱形, 高度是 18 厘米。这个瓶子的容积是多少?)同学们,先独 立思考,再两人交流一下怎样做最简捷。
生: 先求高是 7 厘米的,再求高是 18 厘米的,最后把 它们合起来。π 乘 8/2 的平方,再乘 7 加 18 的和,等于 400π 立方厘米,400π 立方厘米等于 400π 毫升。
3. “倒过来”转化,寻找前后知识联系
师: 同学们,我们用“倒过来”的方法把不规则图形 变成规则图形。在以前的学习中,“倒过来”的方法碰到 过吗?
生: 我记得以前学正方体体积的时候,把不规则物体 放在水里,看它水面上升的高度乘它的底面积。
师: 如果是这样的橡皮泥或者泥,当我们无法计算它 的体积时,我们可以把它放到一个量杯里,一下子看出这 个梨的体积是 250 立方厘米。
片段二:借助斜截圆柱,感悟“倍拼”的转化
1. 自主探索,发现斜截圆柱的转化
师: 上星期我到一个画室看到很多同学在画素描,然 后我看到有一位同学画了一个圆柱,另外一位同学在画这 样一个物体(出示图片)。作为一个数学老师,我想两个问 题,你们猜猜我想哪两个问题?
生: 体积怎么算?表面积怎么算?
师: 这是我想的第二个问题,我还在想左边叫圆柱, 右边叫什么?我回来后问美术老师他不知道,然后我查了 一下,它叫斜截圆柱。观察一下,你能想办法求它的体积 吗?四人小组交流一下。
生 1: 把斜截圆柱放到容器里,看水上升的体积。
生 2: 再弄一个和它完全一样的斜截圆柱,然后把它们 叠起来,拼成一个完整的圆柱。先算出圆柱的体积,再除 以 2.
师: 我们算这个完整圆柱需要知道底面直径和高,底 面直径可以量出来,它的高怎么算?
生: 把最短的一边和最高一边加起来,就是这个完整 的圆柱的高。
生 3: 可以先求出 1 立方厘米的木头有多少重,然后用 这个斜切圆柱的重量去除以那 1 立方厘米的重量,就知道 它有多少立方厘米。
生 4: 把斜截圆柱上面这一段切掉,下面是一个圆柱, 上面再补一个跟它完全一样的图形,除以 2 就能算出上面 部分,再加上下面的圆柱。
生 5: 沿着最低点和最高点的中间划一刀,拼成一个圆 柱。这个圆柱的高是最高加最低除以 2.
2. 独立思考,计算斜截圆柱的体积
师: 看来你们的方法可不少,这个斜截圆柱底面直径 是 10 厘米,最高点是 12 厘米,最低点是 8 厘米,你们自 己选一个方法算出它的体积。
生: π 乘 10/2 的平方,再乘 8 加 12 的和,再除以 2 等于 250π 立方厘米。
师: 猜一猜他是用哪种方法计算的?
生: 他是把两个完全一样的斜截圆柱拼成一个完整的 圆柱体,再除以 2.算出一个斜截圆柱的体积。π 乘 10/2 的平方是这个圆柱体的底面积,8 加 12 的和是这个圆柱体 的高。
3. “倍拼”转化,寻找前后知识联系
师: 同学们,刚才我们算这个斜接圆柱体积的时候,转化方法是找一个完全一样的图形拼成新图形。在小学阶 段学过的数学里,你回忆一下有没有碰到过这样的“倍拼” 转化?
生 1: 我们学梯形的面积的时候是把两个完全梯形拼起 来,这个梯形可能是一个正方形、一个平行四边形或者是 一个长方形。
生 2: 我们学三角形面积的时候,把两个完全一样的三 角形拼起来变成正方形、长方形或者平行四边形,把它们 除以 2 就是三角形的面积了。
片段三:借助三角形面积,感悟“添补”的转化
1. 独立思考,计算三角形面积
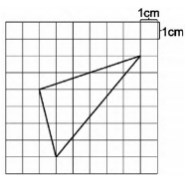
师: 同学们,如果你的学习过程留下的只是面积公式, 你的数学是学不好的,你还要学会转化的方法。求三角形 的面积,你会计算吗?试一试吧。
生 1: 我把三角形分成两个上下三角形,上面三角形的 高是 2 厘米,底是 4 厘米;下面三角形的高是 4 厘米,底 是 4 厘米。这个三角形的面积是 4×4÷2 + 4×2÷2=12(平 方厘米)。
生 2: 这样做是不对的,这条底不是 4 厘米,比 4 厘米要长一些。我是这样做的:我在三角形的外面框了一个正方形,用正方形的面积减去 3 个三角形的面积就是这个三角形的面积。3 个三角形的面积分别是 6×2÷2=6(平方厘米),4×1÷2=2(平方厘米), 5×6÷2=15(平方厘米),所以中间三角形面积是 6×6 - (15 + 6 + 2)=13(平方厘米)。
生 3: 我们可以框出一个梯形,用梯形的面积减去 2 个三角形的面积。梯形面积是(1 + 6) ×6÷2=21(平方 厘米),2 个三角形的面积分别是 2×6÷2=6(平方厘米), 4×1÷2=2(平方厘米),所以中间三角形面积是 21 - 6 - 2=13(平方厘米)。
2. 跨界领域,寻找各种转化方法
师: 我们今天学习了转化的解决问题的策略,转化 的方法是多种多样的,比如,把瓶子倒过来,拼一个完 全一样的图形,把它补成一个新图形等。在计算中我们也经常用到转化,小数乘小数我们把它转化为整数乘整数,异分母分数加减法我们把它转化为同分母分数再计算。你还想到 什么?
生: 我们简便计算 99 乘 99 的时猴,把 99 看成 100 来计算。
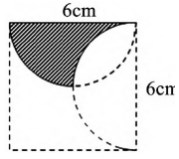
师: 转化在数学中到处都是。你能用转化方法求阴影 部分的面积吗?
【教学赏析】
朱老师在这节课中的教学理念深深点醒了我,我们不 仅要让学生获得基础知识和基本技能,更要发展学生的数 学核心素养。
一、获得数学思想方法,形成数学核心素养
《义务教育数学课程标准(2022 年版)》中指出:学生 的学习应是一个主动的过程,认真听讲、独立思考、动手 实践、自主探索、合作交流等是学习数学的重要方式。学 生获得数学活动经验和形成数学核心素养需要教师在平时 的数学课堂上日积月累地渗透,比如,在教长度单位、面 积单位和体积单位这类课时,要让学生在动手操作中形成 长度单位、面积单位和体积单位的概念,发展他们的量感; 又如要在教学平行四边形、三角形和梯形面积计算这类课 时,让学生通过丰富的操作活动,体会和运用转化的思想 方法,获得转化的基本活动经验。
这样,学生才会在这节 “圆柱的解决问题”中想到不 同的解决问题的方法,串联起前后知识的不同转化方法, 实现活学活用的效果。
二、鼓励学生独立思考,延长学生思考时间
数学学习是学生个体利用已有知识和生活经验去探索 和解决未知问题的过程,不仅能帮助他们发现解决问题过 程中的不足,还能让他们感受到解决数学问题的成功感。 在数学学习过程中,教师要舍得花时间让学生安静地思考, 学会从不同角度寻找问题的正确答案,不应该过早地给予 提示,阻碍他们的思考。
在朱老师的数学课上,他出示题目问题后先让学生安 静地读题,理解题目的意思和要求;再给予学生充分的时 间让他们思考,独立完成解题过程;最后是全班汇报,当汇报过程中学生出现歧义时,他会组织学生四人小组交流 自己的想法,从他人的解题思路中寻求启发。这样,当学 生在独立作业或单元测试时,他们才会静下心来独立思考, 从不同角度的思考中想到正确的解题方向。
三、减少重复机械训练,创设新的问题情境
“熟能生巧”是指学生经常面对同样情境的题目时会非 常熟练,提高了这类题的解题速度和正确率;但“熟能生 笨”是指学生面对同样的题目时,他们只是凭借记忆解题, 缺乏了新的思考和探索。在朱老师的数学课堂上,他围绕 转化思想,创设了各种丰富的情境,利用不同的题目串联 起了倒过来、倍拼、添补等不同的转化方法,还从“空间 与图形”领域跨界到“数与代数”领域,帮助学生整体把 握数学知识的结构。
总之,朱老师创设了具有真实性、挑战性和复杂性的 任务情境,让每个学生都享受安静的思考时光,经历了最 初的“想不到”到中期的“想错了”到最后的“想对了” 的过程,他们或通过自己的思考解决一类题,形成数学思 想方法和数学活动经验;或在他人的分享中突然顿悟,找 到自己“想不到”或“想错了”的问题根源,修正和完善 自己思考过程中的知识漏洞。
参考文献:
[1] 苏芹 . “圆柱的体积计算公式及其应用”教材简析 与教学建议 [J]. 小学数学教育,2021(Z2):84-86.
[2] 曹海娟 . 多元建构,让思维渐次深入—— “圆柱解 决问题”教学实践与思考 [J]. 小学数学教师,2018(01): 36-40.
[3] 朱丽红 . 关注核心内容让数学复习课增值—— 以苏 教版六下《圆柱和圆锥的整理与复习》的教学为例 [J]. 江 苏教育,2019(49):54-56.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/55122.html