摘 要 :随着我国课程改革的持续推进，对教学质量的要求也正不断提升，数学是三大主课之 一，其对于提高学生的成绩、逻辑思维等皆具有重要意义. 但由于传统的“题海战术”已很难满足现 代高中数学的教学需求，因此，高中的数学教师应当对自己的教学方式、方案等进行改善，不断提升 学生的解题能力，为学生的高考奠定基础. 本文主要阐述在高中数学解题过程中，采用转化思想的 作用和方法，并以实例对所提出的方法进行佐证，希望能为有关人员提供参考.
关键词 : 高中数学;转化思想;解题;方法策略
高中数学的教学重点不仅仅只是让学生掌握数 学的基本知识和理论 ,其实践性和难度都比初中数 学高得多 , 因此 ,在高中数学的教学过程中 ,不应只 让学生通过“刷题”来提升自己的解题能力 ,教师应 将数学思维、数学思想融入教学过程中 ,让学生能够 捕捉到解题的方法、重点、思维 ,快速高效的进行解 题. 转化思想是数学解题思想的重要思想 ,其可将复 杂的问题简单化 ,陌生问题熟悉化 ,有助于学生思维 严谨性的提升 , 良好的解题习惯也会随之逐渐形成 , 进而能撬动学生的思维 ,在启智明理中促进学生自 主学习 ,从而提高教学质效.
1 转化思想在高中数学解题中的意义
高中数学题目(尤其是理科数学) 的难度和抽 象性皆明显高于初中数学 ,学生在解题过程中 ,教师 可以将转化思想运用于解题过程中 ,进而达到快速 解题的目的. 转化思想要求学生通过侧面或反面整 理解题思路 ,寻找突破口 ,把复杂、抽象、困难的问题 转变为成一个或若干个自己熟知的或能解决的问 题. 在学习数学的过程中 ,大部分学生会将一个较难的问题通过分解、变形、代换、平移、旋转、伸缩等多 种方式 ,将之转化为一个或几个自己熟悉的基本的 问题 ,从而求出答案. 在解答一元二次方程时 ,学生 可以将一元二次方程通过因式分解转化为一元一次 方程.
2 在数学解题过程中利用转化思想的策略
2. 1 将复杂问题简单化
复杂问题简单化 ,可以是一个数学公式 ,一个数 学概念 ,一个数学定义 ,也可以是有关数学公式的记 忆 ,数学定义的证明等等. 下面我就如何简单数学问 题说我的几点看法 : 一、用自己熟悉的、精简的语言 阐述数学概念和定义. 这样有利于加强概念、定义的 理解和记忆. 比如 ,在我讲抛物线方程的时候 ,抛物 线方程与焦点位置有密切关系 ,抛物线方程一次项 即是焦点所在位置. 而切抛物线的焦点与抛物线方 程的系数的四分之一倍数有关. 这里我用自己的语 言向同学们总结. 抛物线的方程要么是 x2 等于好多 y ,要么是 y2 等于好多 x ,这主要就看焦点位置了 ,如 焦点在 x 轴 ,一次项就是 x ,所以方程就是 y2 等于好多 x. 以次类推. 当面临一道结构复杂直接解答会难 以上手的问题时 ,可将该问题划分为一个或多个简 单的问题 ,逐个解答. 例如以下题目 :
2. 2 将常量转变为自变量
变量转化多用于含有 X 未知数的不等式问题 , 在做该类题目时 ,需根据题目的条件求出参变量的 取值范围 ,虽然该类题目的做题方法多 ,即 :对其分 类讨论、数形结合、分离参数、利用函数性质 ,但次过 程较为复杂 ,出错了较高 ,若能使用变量转化则可事半功倍. 例如以下例题 :
例 1 设 a ,b 是两个实数 ,A = { (x ,y) ∣ x =n , y =na +b ,n ∈ z } , B = { (x ,y) ∣ x =m ,y =3 m2 + 15 ,m ∈z , }C = { (x ,y) ∣ x2 +y2 ≤ 144 }是否存在 a ,b 使得 ( 1 )A ∩ B ≠ ;(2) (a ,b ) ∈ C 同时成立.
方法一 假设存在(x ,y) ∈A∩B ,则相应的直线 y =ax +b 与抛物线 y =3x2 + 15 有公共点.
即 :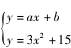 
得 3x2 +15 =ax +b
△ =a2 -12(5 -b ) ≥0 ,即 -a2 ≤12b -180 ,a2 +b2 ≤ 144 两不等式相加得 b2 ≤ 12b -36 ,即 (b -6)2≤0 ,故 b =6. 把 b =6 代入得 a2 ≥108 与 a2 ≤108 . 所以 a2 =108 ,所以 a =6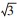 
或 a = - 6 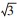,b =6. 再代入原方程得 3x2 ± 6 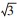+9 =0 解得 x = ± 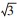∉ Z ,所以 a ,b 不存在.
方法二 当然对于式子 3x2 + 15 =ax + b 即 ax +b - (3x2 +15) =0 ,则式子 ax + b - (3x2 + 15) =0 可看作以 a ,b 为变量的直线方程 ,又因为(a ,b ) ∈ C 即 a2 +b2 ≤144 也可看作以 a ,b 为变量的圆及圆内的点 ,探究该直线与圆的位置关系圆心到直线的距
离 :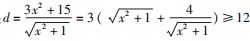
(但当且仅当
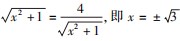时取等号而x∈z 但 ± 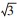∉z ,所以 a ,b 不存在.
分析 以该题为例 ,解法一采用 X 为变量 ,带 入过程较为复杂 ,计算量大 ,学生在解题的过程中 ,容易出现作物;而解法二是将 a、b 等转变为变量 ,将 X 作为常量 ,转化思维 ,解题过程简单易懂 , 由此看 出解决此题选 a ,b 为变量 ,x 为常量同样是可以找 到一种优质的解法. 如何设定主元 ,对学生的思维能力的要求较高 ,主元选定之后 ,有助于用方程或函数 思想来解决问题.
2. 3 将抽象问题形象化
学生在解答抽象问题时 ,往往会出现找不到解 题思路的情况 ,尤其是函数问题 ,此时便可采取抽象 问题形象化的解题方法解决 ,将抽象问题形象化主 要有换元法、凑合法、待定系数法、利用函数性质 法等.
2. 3 . 1 换元法
即用中间变量表示原自变量 x 的代数式 ,从而 求出f(x ) ,这也是证某些公式或等式常用的方法 ,此法解培养学生的灵活性及变形能力.
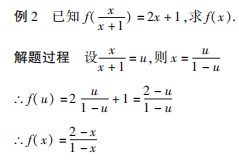
分析 该问题从直观上将属于一道抽象函数问题 ,常规的方程解法其过程相对抽象和复杂 ,设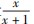
=u ,x 换为 u 采用抽象问题形象化 ,能够将难题、怪 题或超出课程范围的题目转化为简单、熟悉的问题 , 将问题形象化 ,方便解题.
2. 3 . 2 凑合法
该方法是在已知f(g(x ) ) =h (x )的条件下 ,把 h (x )并凑成以 g(u )表示的代数式 ,再利用代换即可求f(x ). 此解法简洁 ,还能进一步复习代换法.
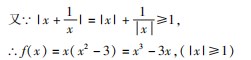
2. 3 . 3 待定系数法
先确定函数类型 ,设定函数关系式 ,再由已知条件 ,定出关系式中的未知系数.
2. 3 . 4 利用函数性质法
主要利用函数的奇偶性 ,求分段函数的解析式.
例题 已知 y =f(x ) 为奇函数 , 当 x > 0 时 , f(x ) =lg(x +1) ,求f(x ).
解析 ∵ f(x )为奇函数 ,
∴ f(x )的定义域关于原点对称 ,故先求 x < 0 时的表达式.
2. 4 静态问题动态化
部分数学问题在以静态的思路进行解题可得出 结果 ,但过程复杂 ,学生在做题过程中容易出错 ,因 此 ,在做该类题目时 ,可将静态问题动态化 ,即 :通过 研究变动情况对题目可能出现的特殊情况进行分 析 ,进而简化解题过程 ,防止错误的发生.
例 5 设 F1 ,F2 为椭圆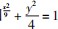
的两个焦点 ,P为椭圆上一点. 已知 P ,F1 ,F2 是一个直角三角形的三个顶点,且
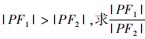的值.
分析 改题目的直角位置为得到确定 ,因此 ,在 解题过程中 ,我们需要先确定直角可以确定的位置 , 在以分类的方式对直角的位置进行确定 ,最后对所 有可能出现的可能进行汇总 ,进而得出范围. 解答问 题则可要让 ,F1 和 F2 动起来 ,对其进行分类讨论 ,以 提高解题的效率.
转化思想是数学解题思想中的重要部分 ,其可 将复杂的问题转化为简单问题 ,抽象问题转化为具 象问题等 ,可帮助学生提升解题效率 ,降低错误率的 发生 ,对于学生提高成绩具有重要意义. 其次 ,转化思 想可有效锻炼学生的思维逻辑能力 ,提升其做题的严 谨性 ,进而使其做事的思维能力、严谨性得以有效提 升 ,为其未来的发展奠定坚实基础. 因此 ,高中数学教 师在教学过程中 ,应将该思想广泛运用 ,帮助学生领悟 解题方法 ,掌握解题能力 ,为其高考提供坚实保障.
参考文献 :
[1 ] 王萍，周顺珍. 关于转化思想方法在高中数学解 题中的应用探讨[J ]. 数学之友，2019 (01 ) :49 -50 .
[2 ] 吴晔. 转化思想在高中数学解题中的应用[J ]. 数学大世界(下旬)，2018 (09 ) :69 +68 .
[3 ] 陈铿熙. 巧借转化思想，让高中数学解题“柳暗 花明”[J ]. 福建中学数学，2019 (05 ) :40 -41 .
[4 ] 郭婧涵. 转化思想在解题中的应用[J ]. 中学数 学教学参考，2017 (27 ) :56 .
“产出导向法”是文秋芳教授创建的旨在改进中... 详细>>
如何设计有效的环境治理政策, 是学术界和政策... 详细>>
