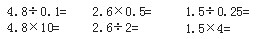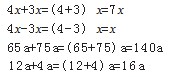SCI论文(www.lunwensci.com)
摘 要
小学阶段的数学教学要时刻关注学生各方面能力的培养,如注意力、适应力、创造力、抗挫力等。其中,洞察力的培养尤为 重要。敏锐的洞察力可以让学生在学习过程中不迷路,透过“看得到”的部分,感知“看不到”的内涵;明白“看不见”的内涵 决定了表象,逐渐揭开事物原本的面貌,明白知识之间的前因后果和脉络走向。因此要用不同的方法去培养学生的洞察能力,从 细微探究到纵观全局,让学生的思维得到延伸,从而构建数学模型。
[ 关键词 ] 小学数学课堂 洞察力 思维 探索学习
小学生学习数学的过程就是一个打开并探索未知世界 的过程,在无数次的上课、听课、评课过程中,笔者感觉 到,不少课堂教学“教师只管教,学生只管受教”,时间长 了,学生就自然地习惯了这种接受型的学习模式,他们的 学习能力得不到有效提高。陶行知先生曾坚定地说过:教 学的核心问题是“教学生学”,教学过程要以过渡到学习过 程为目的地。的确如此,学生的内心世界很丰富,教师的 任务就是引导学生通过自己敏锐的洞察力去探索学习,从 而产生巨大的能量,这种能量可以让人产生多种发展的可 能,使他慢慢“变成他自己”。
洞察力的培养并非一朝一夕,它是学习者深入了解事 物或探究问题本质的能力,学生的洞察能力强弱异势,好 奇与探究是他们的天性,这一天性恰恰说明了他们对周围 世界那么多的惊异和无数的提问。作为教师,培养他们深 层次的洞察能力义不容辞,所以,小学阶段的数学课堂, 应当是在教学中融进对学生洞察能力的追寻和开发。
一、对比:在数学学习中关注思维的延伸
(一)着力对比,凸显思维的求异存同
培养小学生的思维方式有很多,比较、类比、抽象、 概况、猜想和验证等都可运用于实践。课堂中、习题中, “比较”是很常见的思想方法之一,它需要学生运用一定的 经验和积累进行,多次运用“比较”的方法也能促进学生 的思维得到很好的延伸,同时,他们的洞察能力在“比较” 中悄无声息地被培养和激发起来。例如,在教学小数乘除 法之后,根据教材安排,学生尝试按题组计算填写得数:
不难发现,让学生在一组一组的计算地时候,他们的 洞察力被激发成“启动”状态,他们在尝试完成了第一组 题之后似乎是尝到了“甜头”,迫不及待地想要去尝试第二个题组,好证明自己第一次洞察到的“小秘密”。学生边做 边在观察着、思考着,根据自己的洞察力和理解力发现每 个题组包含的一些规律。部分学生会发现:一个数 × 比 1 大的数 = 积(大于原数),一个数 × 比 1 小的数 = 积(小 于原数);一个数 ÷ 比 1 小的数 = 商(大于被除数),一个 数 ÷ 比 1 大的数 = 商(小于被除数)。随后,教师有层次 地引导交流:“还有什么规律?”“题组式子的数字之间有什 么关系?”通过比较,学生会发现两个式子中乘除号后面的 两个数的乘积竟然都是“1”。在交流、辨析中把刚才自己 洞察出来的规律与其他同学洞察出的结果进行结合,教师 再帮着梳理提升,抽象概括出完整的结论,建立数学模型。 之后举一反三,出示升华之后的应用:
有了之前的洞察异同、比较挖掘和梳理提升,学生再 来做这类计算题就得心应手了:部分学生会如饥似渴地探 究缘由,部分学生会手不释卷地发现奥秘,可以说,智慧 的大门是学生自己打开了!纵观整个引导过程,既顾及了 一部分分析能力较弱的学生,让他们用自己的洞察能力收 获了自信,同时,也发展了一部分学习能力较强的学生, 他们用强大的洞察力发现规律,总结方法,学生的求异思 维和探究能力均得到了很好的锻炼,大家在比较、合作、 交流中相互促进共同提高,学生的思维始终处于被激活、 准备深挖的状态。
(二)着力选择,凸显思维的辩证平衡
在教学中,教师不仅仅要让学生了解知识的特点,更 要让学生把自己了解到的知识特点和实际要解决的问题结 合起来,辩证地看待问题,做出正确的选择。例如,教学 “扇形统计图”,首先引导学生对比:“之前,我们学过的三 类统计图,条形、折线、扇形统计图各有千秋,你们能说说它们的异同之处吗?”待学生归纳完之后,教师继续深 入:“每种统计图都有各自的特点,我们先要观察数据的特 征,后决定解决这个问题选择哪类统计图比较合适。大家 想一想,若要完成“六年级跳绳达标率的统计”,我们应该 选择何种统计图比较合适呢?”
六(1) 班达标率 90%, 六(2) 班达标率 95%, 六 (3)班达标率 87%,六(4)班达标率 94%。
毫无疑问,这时候学生思维强烈的求知欲被打开,达 标率就是要统计达标人数与总人数之间的占比情况,且要从 图中可以直观地看出数量的多少,便于比较。通过每个学生 敏锐的洞察力和一番唇枪舌剑之后,最终达成一致:扇形统 计图通常是表示部分与部分、部分与整体之间的关系,在 这个题目中比较占优势,但它不能清楚地显示具体的数量, 所以这道题用条形统计图表示比较合适。题中虽然出现的 是百分数,由于各个班级的总人数各不相同,就意味着 4 个 班这些百分数的单位“1”不同,所以不能用同样的圆形表 示整体。通过这样的选择过程,学生分析数据的能力得到了 培养,他们的洞察能力也得到了锻炼和提升。统计图的选择 究竟合适不合适,是对学生思维延伸的开启。选择了适合 的统计图,就便于大家看到有效的信息从而对数据进行分 析和描述,洞察能力的精准度就在不知不觉中被提升了。
二、细化:在数学学习中关注方法的指引
小学生天然地怀抱对世界的好奇,即使在幽暗的环境 下,只要有一丝微弱的烛光—— 旧知铺垫,他们的洞察能 力就会很容易被唤醒,学生会运用自身已有经验探究新知。 所以数学课堂中要巧妙运用旧知识铺垫,让学生在数学学 习中体会数学知识各部分之间存在着密切的内在联系,铺 垫就像体育课前的热身活动,能轻松地唤起学生对新知的 探索欲望,对接下去内容的理解和掌握有指引方向的作用。
例如,数学苏教版五上“化简含有字母的式子”,教 师在第一次磨课时,直接让同学用自己的想法说说为什么 “3x+4x=7x”,班级里顿时陷入了尴尬的安静,等了许久也 未见一个同学有想法。显然,孩子们思维迟缓的原因就在 于他们的洞察力并没有被激活。
第二次磨课,为了使这个知识点更为自然地生长,教 师改进细化,以旧知导入,用细微的变化唤醒他们的洞察 力,让学生在出现问题前就发现问题:
【添正方形】
师: 小芳在他下面摆了同样个数的正方形,正方形摆 了多少个?为什么?
生:x 个,因为摆了同样个数的正方形。
师:是的,在这个问题中,正方形和三角形的个数相 同,我们就用同一个字母 x 来表示摆的个数,也就是摆了 x 个三角形和 x 个正方形。
师:摆正方形用了多少根小棒呢? “4x ”中 “4”表示 什么?“x ”表示什么?“4x ”表示什么?
这些铺垫看起来简单,但是对于孩子而言,要深入事 物或问题,首先要让他们积累很多必要的知识,如 3x 和 4x 的意义,如果不理解这些基础知识,就很难深入下去,就 只能看到事物的表面。所以,这些细节的变化就是在帮助 他们唤醒各自的洞察力,把 3x 和 4x 的意义理解透彻之后, 再让他们用自己的知识证明“3x+4x=7x”,同学们的思维 犹如从黑暗中走向光明,顿时小手如雨后春笋般林立。
生 1: 3x 表示 3 个 x ,4x 表示 4 个 x ,3 个 x 加上 4 个 x 就等于 7 个 x。
生 2: 可以画线段图,先画 3 段,再画 4 段,每段都是 x ,3x+4x=7x。
生 3: 看到这个式子我想到了乘法分配律,把 x 看作是 一个数,在 3×x 和 4×x 中都有一个相同的乘数是 x ,这时 就可以用乘法分配律来计算哦!
细化知识点作为铺垫,是由教到学逐步放手的过程, 很多时候,设计用旧知导入新授课可以实现新旧知识的无 缝对接,让新知的学习在旧知的延伸中发生。其实这个过 程就是教师领着学生在一定程度上还原前人探索和发现这 一块知识的过程,如若多次接触这样的形式,并都能顺利 衔接,那么他们再次遇到类似的情况就轻车熟路了,看穿 事物的“真相”也就不难了。整个过程中,孩子的思维都 是活跃的,尤其是激发出了管理自身知识的能力,方法多 样化,充分挖掘学生已有的知识储备,从而引导学生用旧 知识证明新知识,成为知识、方法、洞察能力的主动建构 者和创造者。
三、提炼:在数学学习中关注重难点的升华
探索一个有研究性的问题比出示一百个答案更重要。 首先,我们要围绕一个核心,提出一个能激发学生共同来 探究的问题,对教学重难点的突破是很有意义的。在这个 突破的过程中,学生聚集思维,融会贯通自己已有的知识 点,探究出各种适合自己的答案,然后同屏汇聚,共同来 洞察每种方法的优点和不足,最后提炼出简单化、精练化的最优方案。
学生的方法有很多,为了对本课重难点进行提炼与升 华,教师开始引导学生洞察所有方法的共同点,那就是这 些方法都是在把“异分母分数”转化成大家已经学过的知 识或方法来思考;再引导学生洞察这些方法的不足之处: ①如果每一个分数都去画图耗费时间且不精准, 比较麻 烦; ②找中介数来比大小局限于部分分数,不具有普遍性; ③转化成小数计算量太大,且计算的时候容易算错……同 学们进行了充分的交流之后,对通分的方法继进行续提炼: “为什么原来不能比的分数通分后就可以比了?”原来通过 通分后就变成了“同分母分数”了,分数单位相同就可以 比较它们的大小了。通分的方法适用于所有分数的大小比 较,这样的提炼,使学生的数学认知顺利生成。在整个探 究过程中,从一开始的用多种方法比较,到后来的比较这 些不同的方法,再到最后的消除疑问,这就是提炼的过程。 这个过程使学生不断地储备与释放他们内在的知识,同时, 他们的洞察能力不断萌芽和不断壮大。
又如在教学苏教版五上“化简含有字母的式子”的时 候,教师让学生找一找刚才解决的这几个问题,得出的四 个式子有没有共同的地方。
课件呈现之前解决的四组算式,让学生自己去发现 “共同的地方”。于是,孩子们开始了各自洞察能力的大 比拼:
生 1: 这些式子中都含有字母。
生 2: 这些式子计算时都运用了乘法分配律。
生 3: 同一个式子中字母不变。
生 4: 同一个式子中数字相加或者相减了。
最终进行汇总提炼,得出“化简”的基本方法。孩子 们在讨论中抽象出数学模型,在交流中感悟数学建模的过 程,丰富了从直观向抽象转变的学习经验。学习并没有到 此结束,教师继续深入挖掘孩子的洞察能力,继续提炼:“再观察比较计算前的式子和计算后的式子,你更喜欢哪一 个呢?为什么?”在孩子们发现化简后的式子更为简单之 后,让学生从“3x+4x”和“7x ”中选择一个式子计算 x=9 时的值。教师采用了开放式选择,帮助学生积累解决问题 的经验。洞察能力强的学生,最喜欢的就是这种挑战, 因 为他们有着敏锐的洞察力。在他们的带领下,多数学生都 会发现原来代入化简之后的“7x ”进行计算更简单,真正 做到了活学活用,不断地走向实践世界,整个提炼的过程 成就了有价值的学习!
四、梳理:在数学学习中沟通联系、构建模型
教师在实施课堂教学的过程中,要考虑本节课的学习 对学生的能力发展有什么潜在的价值,学完这节课之后, 对学生的个人发展有无助推作用,对学生的关键能力有什 么指引作用,甚至是对社会发展需求有什么贡献,作为教 师要经常创造生生对话的机会,鼓励学生走上讲台、自信 地表达、勇敢地质疑,让学生掌握学习的主动权,有明鉴 万里的经验。教师做一个倾听者,不急于点破,不急于总 结,不急于练习,等待学生更强烈的洞察力迸发出来再沟 通,主动发现,体验自由构建模型的乐趣,因为学生的参 与、体验、建构才是数学思维形成不可或缺的过程。
比如学习完“多边形的面积”之后的整理与练习,通 过梳理之前学过的平面图形——平行四边形、三角形、梯 形的面积公式的推导过程有什么共同的地方,孩子们自然 会深度洞察推导方法、过程和相互之间的联系,发现这些 推导过程都是把未知的知识转化为已知的内容,再由已知 的内容推导出未知的公式,真正体验到了转化思想和模型 思想,全面地、系统地建构面积计算的知识体系。
五、结语
唤醒学生的洞察力,是小学数学教学不可或缺的培养 使命,敏锐的洞察力不是天生的,而是在实践和活动中训 练培养出来的本领,是不断地思考、总结、凝练从而轻易 拿捏的产物,即使在新情境中,也可以瞬间反应的能力。 第一片树叶凋落,我们就闻到了秋天来临的味道;第一只 小手高高举起,我们就看到了他们能力提升的细微迹象。 数学教学不就是需要我们培养学生具有这种一叶知秋的洞 察能力吗!
参考文献:
[1] 武维民,张秋爽 . 跟吴正宪学教数学 [M]. 上海:华 东师范大学出版社,2019.
[2] 孙朝仁,孙焱 . “教、研、写”一体化 [M]. 南京: 江苏凤凰教育出版社,2019.
[3] 成尚荣 . 儿童立场 [M]. 上海:华东师范大学出版社, 2018.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/54727.html