SCI论文(www.lunwensci.com)
【摘要】算理是小学生在数学学习中的重要内容。笔者结合自身亲历的教学实践 ,探讨小学数学算理教学的 一些设计及策略 。在模仿中 ,帮助学生初步理解和认识算理;在说理过程中 ,让算理学习更有深度与广度;在纠 错中 ,优化算理思路;在题组训练中 ,搭建算理理解的阶梯;在变式中 , 内化算理知识理解算理本质。
【关键词】算理教学,小学数学,教学策略
小学生学好算理知识将为日后的其他数学知识 的学习打下良好的基础。算理教学是学生深化理解算 理的过程 ,是巩固和应用算理算法的过程 。算理知识 的学习和练习过程 ,也是学生思维训练的过程 。在教 学实践中 ,有时过多地追求算法多样化 ,增加估算教 学的内容等措施 ,造成部分学生没办法在短时间内及 时掌握当天所学的算理知识;或者会准确运算 ,却不 知道其中的算理 , 没法形成一个完整的知识系统;或 者没能灵活运用算理算法解决实际问题;更多的学生 是算理本质理解不透彻 , 口算速度慢 ,正确率下降。因 此 ,算理教学的设计与选择 ,对学生的算理知识的掌 握有很大的帮助。
一、模仿,是对算理的初步理解和认识
多年以来 ,模仿一直被认为会造成学生能力的降 低 ,很多人都很排斥“模仿”在学习中的应用 ,抑制学 生的模仿行为。在小学阶段 ,学生的年龄小 ,感性模仿 力强 , 可以快速模仿对象的外部特征及行为动作 ,他 们在学习过程中 ,常常会不自觉地无意识地对事物的 外表和动作进行模仿。改善模仿训练的质量 ,可以提 高学生的学习质量。
例如教学乘法分配律 43×17+57×17 时 , 有一部 分学生还不太理解 43×17+57×17 表示“43 个 17 和 57 个 17 的和”,学习时他们会先依照教材上的描述和操 作程序 ,结合教师的讲解及示范的活动步骤 ,通过模 仿来完成第一次的练习 。在接下来的交流讨论中 ,其 他同学一系列语言与动作演示下 ,学生在继续模仿中 初步理解到“在算两个数分别与第三个数相乘再相加 时 ,可以先算两个数的和 ,再算与第三个数的积 ,这样 做更简便”。再做类似的题目时 ,学生就会在头脑中出现前期产生的表象 ,乘法分配律的运算技能就得到科 学地迁移 。这时的模仿是一种仿效 ,是对解题规则的 准确复制。学生从中积累乘法分配律的数学知识与技 能 ,从而形成经验;也促进心智模式的自觉调整 ,主动 学习算理知识 ,让自己成为算理学习的主人。
在算理学习中 ,学生如果不理解算理 ,不能熟练 掌握法则 ,直接导致学生在计算中存在很多问题 。要 使学生的运算能力有个质的飞跃 ,必须让学生深刻理 解算理 ,而且还得在理解算理中精准地记忆 。小学数 学课本中的例题与练习的设置常常是有关联的 ,那些 关联就是便于学生在模仿练习中 ,实现对算理理解和 记忆的最佳方法。
二、说理,让算理学习更有深度与广度
在课堂上 ,这样的场景你有经历过吗? 教师提出 一个问题 ,请第一个学生回答 ,得到的答案不满意 ,迫 不及待请下一个学生起来回答 , 得到的答案又不满 意 ,再来一个学生继续回答 ,似乎仍然不满意 ,继续请 下一个学生回答 ,终于说出了教师预设的答案 ,教师 心里松了一口气 ,说:“给他掌声。”啪-啪-啪!接着讲 下一题了 。这时的学生确实得到了正确的答案 ,却留 下一脸的茫然 ,刚才那些答案为什么是错的 ,为什么 只有最后一个答案是正确的 。没来得及细想 ,下一题 又得开始了。长久下去 ,学生对知识背后的原理掌握 不到位 ,解题思维不灵活 ,不利于学生对数学能力的 提高和培养。小学数学算理课堂教学中 ,说理是对算 理知识的逻辑性的展示 ,教师利用有条理的说理进行 算理教学 ,创设说理契机。如学习“408×12”时 ,408 中 间的 0 可以省略吗? 为什么? 教师留给学生说理的时 间 ,学生会得出很多与众不同的想法 ,在交流讨论中锁定理由 ,对因数中间有 0 的乘法算理算法的形成具 有重要的启发。
又如 ,在学习 2.35 ×3 时 ,教师请学生在黑板上板 演 ,集体订正结果之后:
师:小数乘整数是怎么计算的?
生:把 2.35 扩大 100 倍 ,算 235×3=705 ,705 缩小 100 倍是 7.05 ,所以 2.35×3=7.05.
师:你从哪里知道扩大 100 倍啦?
生:2.35 里有 235 个 0.01.
师:你听得真认真 ,请你把刚才的过程再说一遍?
生:235 个 0.01 乘以 3 , 得到 705 个 0.01 , 就是 7.05.
在教师的适时引导下 ,学生发现小数与整数之间 是有联系的 ,而且还可以转化 ,引导学生从简单的参 与转化为带着思考的参与 ,“为什么可以这样转化? ” “是怎样转化的?”揭示出小数乘整数的发展和形成的 根据 。说理中 ,理解并掌握了小数乘整数都是先转化 成整数乘整数来计算的 ,找准算理的“源”与“流”。学 生更是在思考、讨论、交流、倾听中 ,让小数乘整数的 算理学习更有深度与广度。
课堂上说理的目的是将所学的算理知识与学生 自身的思维进行碰撞 , 借助学生已有的学习生活经 验 ,通过自己的语言及思维方式 ,探析算理与客观事 物或以前的定律、规律之间的关联 ,教会学生透过现 象理清算理知识的本质 ,从多方面思考问题 ,养成追 根究底的习惯 ,拓宽学生联想的空间 ,充实算理的教 学内容 ,更加深入地探寻算理 。让学生与教师一起承 担“说理”的角色 ,激发学生的说理热情 ,在师生之间 和生生之间的争辩中 ,激活思维 ,体验说理过程的趣 味性 ,是转变算理知识输出的一种有效途径 。不能为 了节约时间 ,按时完成起初制定的教学计划 ,采取填 鸭式的满堂灌 ,或者只是教师一个人在说理 ,这样的 说理是多么无趣 ,无法引起学生的共鸣 ,只会降低算 理知识的讲解及学生的基础能力。
三、纠错,是一种优化算理思维的过程
错误是一种经历 ,也是一种学习 。只要有学生成 长的地方 ,就会有学生出错的地方 。而学生出错的地 方恰恰真实地反映了学生学习过程的心理。有些还包 含着学生创造性的东西。如果此时的教师一味地埋怨 学生上课不注意听讲 ,批评错误 ,那教师也将错过一 次学生的成长机会。不如以“错”为营 ,把学生的错误当作一个问题的情境 ,启发学生从不同的角度审视问 题 ,挖掘错误中的潜在智力因素。
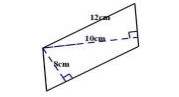
例如 ,计算如下平行四边形的面积。
有个学生的结果:12×10=120(平方厘米)
当学生的答案一出现 , 其他学生就开始窃窃私语 。学生对自己的解题过程也开始了怀疑 ,“自我否 定”与他原有的知识观念开始冲突 ,促使他对已完成 的思维过程进行一次周密而批判性的再思考。他来了 一句“老师 ,我反悔了。”“为什么想反悔? ”“算平行四 边形的面积时 ,必须用底和它对应的高相乘 。而我刚 才的 10 不是 12 对应的高。”学生通过错题反思 ,意识 到“错误”的根本原因所在 ,对平行四边形的面积的计 算有了一次重新思考 ,对先前的认知进行了一次新的 构建 ,成功地实现了对算理思维的一次优化 。既有利 于问题的解决 ,也促进学生认知水平的发展。
在课堂上 ,教师有针对性地讲解学生现场生成的 错题 ,不仅使出错的学生本人有一种自我反思 ,其他 学生也会产生一种小小的触动 , 并会迅速集中注意 力 ,关注错题 ,在好奇心和好胜心的驱动下 ,会对错题 进行评价。这时学生的意识里会有“为什么我们的运 算符号或过程会不一样?”“区别在哪里?”“错在哪?” “怎样运算才是正确的? ”等等一系列问题 , 由师生之 间和生生之间的互动中 ,挖掘出错误中潜在的智力因 素 ,对问题进行一种自主剖析 ,使学生明白其中存在 的问题 ,认知结构得到重新平衡 ,优化算理思维的过 程。
四、题组,是搭建算理理解的阶梯
在教学中 ,通常会发现很多题目之间是有内在联 系的。有的题型结构相似 ,有的数量关系一样 ,有的解 题方法相同 ,等等。教师根据这些题目特点 ,经过有效 的编排 ,使得几个问题前后存在着联系 ,或解决一系 列问题的方法发生变化 , 引导学生挖掘问题的本质 , 找到问题的规律。帮助学生巩固知识的算理算法 ,拓 展思维 ,用“练一组题 ,通一类题”的效果 ,代替“题海 战术”。
例如 ,23×3 23×12 123×12 123×112
(1)请列竖式完成上面算式。
(2)说一说 ,你是怎样算 23×3 和 23×12 的? 这两 个算式的结果有联系吗?
(3)你还能找出其他有联系的两个算式吗?
(4)你还会算 1234×12 吗? 1234×112 呢?
通过这组题目 ,以 23×3 训练旧知 ,作为新知 23× 12 的切入口 ,成为突破难点 ,形成算理算法的重要途 径 。用四个层级问题来引领学生计算、观察、对比、分 析 ,思考:23×12 里有 4 个(23×3) ,23×12 比 123×12 少 了 100 个 12 , 123×112 比 123×12 多了 100 个 123.每 两个算式之间的联系又是如何分别在竖式中体现出 来的? 学生在边计算边思考中 ,理解了多位数乘法的 算理 ,第(4)小题 1234×112 的计算 ,学生也能独自顺 利解决了 。这些层级问题让学生从“会计算”走向“会 推理”的一种创造性思维 ,让隐性规律显性化 ,抽象算 理具体化 ,算理知识过程化 。同时彰显了题组所蕴涵 的数学思想、数学方法、学习策略等价值 ,做到“题”尽 其用 ,最大程度提高题组练习效率。
精简又综合的题组 ,就好比是学生学习算理知识 过程中的一个梯子。这些算理题组 ,有的描述不同 ,有 的情景不同 ,有的呈现方式不同 ,但解决的策略、思路 和本质却是相同或相似的;而有的情景相同 ,却关系 不同 ,或意义不同 ,或本质不同 。这些似是而非 ,似同 非同的题目编为题组 ,就如按难易程度设计成层层递 进的梯子 ,也可设计成对比型的梯子 ,还可以设计成 互逆型的梯子。学生沿着台阶一步一题 ,一步一步地 向上走 , 在掌握与解决单个算理之外 , 通过比较、辨 析 , 了解各算理的本质 ,沟通几个算理规律前后的联 系 ,帮助学生头脑中形成一个稳固的算理知识系统。
五、变式, 内化算理知识理解算理本质
在数学学习中的变式 ,是对题中的各种感性材料 变换表现形式 ,在各种表现形式中突出数学恒在的本 质特征 ,只变换事物的非本质特征 ,帮助学生提高对 算理内在本质和规律的掌握能力 ,在学生内部形成一 种相对较稳固的算理和算法 ,对内化的算理知识系统 化 ,实现对学生数学素养的综合培养。例如:
原题:有一张梯形卡片 ,上、下底的和是 28 厘米 ,高是 8 厘米 ,则这张卡片的面积是( )平方厘米。
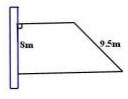
变式:学校靠墙围了一块科技种植园(如图) ,一共用了 37.5米长的篱笆。这块科技种植园的面积是多少平方米?
变式后 ,求科技种植园的面积其实就是求梯形的 面积 。上底和下底的和需要用 37.5 米的篱笆长去掉 9.5 米。这些已知条件变得更为感性 ,而与原题的题型 结构和数量关系 ,甚至解题方法都没有变 ,学生思想 有了一个很好的活动条件 ,使学生深刻地理解求梯形 面积需要知道所求梯形的上底与下底之和及高 ,帮助 算理知识的内化。
练习时 ,学生的参与度很高 ,在展示和表扬中找 到了学习数学的自信。感受“变”与“不变”的快乐 ,战 胜思想的僵化与惰性 ,培养了思维的创新 ,领略着数 学的无限魅力 ,学习数学的兴趣就更浓了 。同时为学 习乘法分配律做好了铺垫。
算理题目是永远做不完的 ,变式教学是一种很不 错的新尝试 , 它会让算理知识的呈现方式更为多元 , 增进学生对算理知识的多角度的理解与认知;在“不 变”与“变”中启发学生思考 ,拓宽学生的思维 ,并让算 理知识得到很好的延伸;把复杂的算理知识简单化 ,让 学生更容易体验成功的快乐等 。在算理教学中 ,算理 学习资源的积极利用 ,从不同角度、不同层次和不同 背景的变化去分析算理知识的变式 , 去说明算理 ,有 意识地启发学生去除非本质属性的干扰 ,从“变”的想 象中 ,对学习资源进行审辩 ,再深度加工 ,从中分辨出 本质与非本质属性的区别 ,发现“不变”的算理本质 , 在变式中深刻理解算理知识 ,用以少胜多来提高学生 算理学习效率。
总之 ,算理教学必须点燃学生学习算理知识的热 情 ,挖掘算理课堂的趣味性 , 以引导学生理解算理为 核心 ,让学生经历算理的形成过程 ,深入地研究算理 , 增强算理知识的科学性 ,体会算理所蕴涵的数学逻辑 思维的优越性 ,提高算理教学教育性 , 以积累数学活 动经验 ,提高学生的各种能力。
参考文献:
[1]李德.模仿式学习在小学数学课堂中的应用[J]. 新课程 •中旬,2018(5):13.
[2]顾亚龙 .让题组模块“会说话”[J]. 教育 视界 , 2015(4):13-15.
[3]周晓萍. 以“变”促“活”以“变”入“深”以“变” 求“广”—例谈变式题的设计策略[J].科学大众(科 学教育),2018(11):61.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/51873.html