数学建模视角下对 2022 年高考卷剖析论文

 

SCI论文（www.lunwensci.com）：

　　摘  要 :本文主要从 2022 年高考卷试题入手剖析 ,从数学建模视角洞察其命题目的 ,剖析高考 题本质原理 ,挖掘数学建模这一核心素养导向 ,夯实基础 ,理解数学本质 , 引导学生形成数学知识系 统 ,助力高三备考.

　　关键词 :核心素养;数学建模;建模情景;模型构造;模型还原

　　数学建模作为核心素养的一项关键部分 ,在处 理分析实际问题时往往可以做到事半功倍. 如果能 把问题进行模型化 ,数据就可以可视化 ,图形就可以 立体化. 本文以 2022 年高考题为例剖析数学建模本 质 ,进而有效培养学生的建模思维.

　　1 建立模型构造

　　高中数学建模构建的核心就是几何与代数有机 融合. 突破数学代数结构特征与几何知识相关 ,能够 从数学问题挖掘、构建几何模型去解决.

　　例 1    (2022 年新高考 Ⅰ 卷第 4 题) 南水北调 工程缓解了北方一些地区水资源短缺问题 ,其中一 部分水蓄入某水库. 已知该水库水位为海拔 148 . 5m 时 , 相 应 水 面 的 面 积 为 140 . 0 km2 ; 水位为海拔157 . 5m时 ,相应水面的面积为 180 . 0 km2 ,将该水库 在这两个水位间的形状看作一个棱台( 如图 1 ) ,则 该水库水位从海拔 148 . 5m 上升到 157 . 5m 时 ,增加 的水量约为( 7 ≈2. 65)(       ) .

　　A. 1 . 0 × 109 m3                    B.  1 . 2 × 109 m3

　　C.  1 . 4 × 109 m3                  D.  1 . 6 × 109 m3
 

图　1

　　解析  依题意可知棱台的高为 MN = 157. 5 - 148. 5 = 9( m ) ,所以增加的水量即为棱台的体积 V.

　　棱台上底面积 S = 140. 0km2  = 140 × 106 m2 ,下 底面积 S′ = 180. 0km2  = 180 × 106 m2 ,

　　所以 V =h (S + S′ +)

　　=  × 9 × ( 140 + 180 + ) × 106 = 3 × ( 320 + 60 7 ) × 106
 

　　≈ ( 96 + 18 × 2. 65 ) × 107

　　= 1. 437 × 109

　　≈1. 4 × 109 ( m3 ) .

　　例 2    ( 2022 年全国高考甲 卷 理 科 第 7 题)

　　在长方体 ABCD - A1 B 1 C 1 D1   中 , 已知 B 1 D 与平面 ABCD 和 平 面 AA1 B 1 B 所 成 的 角 均 为 30 ° , 则(        ) .

　　A. AB = 2AD

　　B. AB 与平面 AB1 C1 D 所成的角为 30°

　　C. AC = CB1

　　D.  B1 D 与平面 BB1 C1 C 所成的角为 45°
 

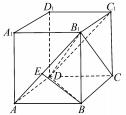
图　2

　　解析  如图 2 ,不妨设 AB = a ,AD = b ,AA1  = c , 依题以及长方体的结构特征可知 ,B1 D 与平面 AB- CD 所成角为∠B1 DB ,B1 D 与平面 AA1 B1 B 所成角为∠DB1A ,所以 sin30° =  = , 即 b = c ,B1 D = 2c=  ,解得 a =  2 c.
 

　　对于 A ,AB = a ,AD = b ,AB =  2AD ,A 错误 ;

　　对于 B ,过点 B 作 BE⊥AB1  于点 E ,易知 BE ⊥ 平面 AB1 C1 D , 所 以 AB 与 平 面 AB1 C1 D 所 成 角 为∠BAE ,因为 tan ∠BAE = 所以∠BAE≠30° ,B 错误 ;

　　对于 C ,AC ==  3 c ,CB1  =  =  2 c ,AC≠CB1 ,C 错误 ;

　　对于 D ,B1 D 与平面 BB1 C1 C 所成角为∠DB1 C ,sin ∠DB1 C = =  = ,而 0 < ∠DB1 C < 90° ,所以 ∠DB1 C = 45°. D 正确.
 

　　故选 D.

　　例 3    (2022 年新高考 Ⅰ 卷第14 题) 写出与圆 x2  + y2  = 1 和(x - 3)2  + (y - 4)2  = 16 都相切的一条 直线的方程_____ .

　　解析  如图 3 , 圆 x2  + y2  = 1 的圆心为 O ( 0 ,0 ) ,
 

图 3

　　半径为 1 , 圆 (x - 3)2   + (y - 4)2   = 16 的圆心 O1   为(3 ,4) ,半径为 4 ,两圆圆心距为 ,等于 两圆半径之和 ,故两圆外切.

　　如图 3 ,当切线为 l 时 , 因为 kOO1  = , 所以 kl  = -  .
 

　　设方程为 y = - x + t ( t > 0) ,

　　点 O 到 l 的距离 d = = 1 ,
 

　　解得 t = .
 

　　所以 l 的方程为 y = -x +  .
 

　　当切线为 m 时 ,设直线方程为 kx + y + p = 0 ,其 中 p > 0 ,k < 0 ,
　　由题意，得

　　解得 k=-

    　　    p=

　　所以 y = x - .
 

　　当切线为 n 时 ,易知切线方程为 x = - 1 ,

　　所以答案为 y = -x +或 y = x - 或 x= - 1 .

　　2 突破建模情景

　　常规问题很难解决时 ,我们通过构建数学模型 , 调整思维角度 ,敢于构想新的问题意境 ,往往柳暗花 明又一村.

　　例 4    (2022 年新高考Ⅱ卷第 12 题) 若 x ,y 满足 x2  + y2  - xy = 1 ,则(       ) .

　　A.  x + y≤1          B.  x + y≥ - 2

　　C.  x2  + y2 ≤2        D.  x2  + y2 ≥1

　　解析  因为 ab≤() ≤( a ,b ∈R) ,

　　由 x2  + y2  - xy = 1 可变形为

　　( x + y )2  - 1 = 3xy≤3( )

　　解得 - 2≤x + y≤2.

　　当且仅当 x = y = - 1 时 ,x + y = - 2 , 当且仅当 x = y = 1 时 ,x + y = 2 ,所以 A 错误 ,B 正确 ;

　　由 x2  + y2  - xy = 1 可变形为

　　( x2  + y2 ) - 1 = xy≤. 解得 x2  + y2 ≤2.

　　当且仅当 x = y = ± 1 时取等号 ,所以 C 正确 ; 因为 x2  + y2  - xy = 1 变形可得

　　(x - )2  +y2  = 1.

　　设 x -  = cosθ ,y = sin θ ,

　　所以 x = cosθ +sin θ ,y =sin θ.
 

　　因此 x2  + y2  = cos2 θ + sin2 θ + sin θ cosθ
 

　　= 1 +sin2 θ -cos2 θ +
 

　　= +sin (2 θ - ) ∈ [ ,2 ].
 

　　所以当 x =  ,y = - 时满足等式.

　　但是 x2  + y2 ≥1 不成立 ,所以 D 错误.

　　故选 BC.

　　例 5     ( 2022 年 新 高 考 Ⅰ 卷 第 7 题)设 a =0. 1e0. 1 ,b =  1  c = - ln0. 9 ,则(       ) .

　　A.  a < b < c          B.  c < b < a

　　C.  c < a < b           D.  a < c < b

　　解析  设f(x ) = ln ( 1 + x ) - x (x > - 1 ) , 因为 f ′(x ) = - 1 = -  ,
 

　　当 x ∈ ( - 1 ,0) 时 ,f ′(x ) > 0 ,

　　当 x ∈ (0 , + ∞ ) 时 ,f ′(x ) < 0 ,
　　
　　所以函数f(x ) = ln ( 1 + x ) - x 在(0 , + ∞ ) 单调 递减 ,在( - 1 ,0) 上单调递增.

　　所以f() <f(0) = 0.

　　所以 ln - < 0.
 

　　故 > ln  = - ln0. 9 ,即 b > c.
 

　　所以f( - ) <f(0) = 0.
 

　　所以 ln +  < 0.
 

　　故 < e - .
 

　　所以e<
  .

　　故 a < b.

　　设 g(x ) = xex  + ln ( 1 - x ) (0 < x < 1) ,

　　则 g′(x ) = ( x + 1 )ex  +  = . 令 h(x ) = ex (x2  - 1) + 1 ,h ′(x ) = ex (x2  + 2x - 1) ,

　　当 0 < x <  2 - 1 时 ,h ′ ( x ) < 0 , 函数 h ( x ) = ex (x2  - 1) + 1单调递减 ,

　　当 2 - 1 < x < 1 时 , h ′ ( x ) > 0 , 函数 h ( x ) = ex (x2  - 1) + 1单调递增 ,

　　又 h(0) = 0 ,

　　所以当 0 < x <  2 - 1 时 ,h(x ) < 0 ,

　　所以当 0 < x <  2 - 1 时 ,g′(x ) > 0 , 函数 g(x ) = xex  + ln ( 1 - x ) 单调递增.

　　所以 g(0. 1) > g(0) = 0.

　　即 0. 1e0. 1  > - ln0. 9 ,所以 a > c

　　故选 C.

　　例 6    (2022 年全国高考甲卷理科第 16 题) 已 知 x = x1  和 x = x2  分别是函数f(x ) = 2ax  - ex2 ( a > 0 且 a ≠1) 的极小值点和极大值点. 若 x1  < x2 ,则 a 的取值范围是_____.
　
　　解析  由题知f ′ ( x ) = 2lna ·ax  - 2ex.

　　因为 x1 ,x2  分别是函数f(x ) = 2ax  - ex2   的极小 值点 和 极 大 值 点 , 所 以 函 数 f (x ) 在 ( - ∞ ,x1 ) 和 ( x2 , + ∞ )上单调递减 ,在 (x1 ,x2 )上单调递增. 所以 当 x ∈ ( - ∞ ,x1 ) ∪ ( x2 , + ∞ )时 ,f ′ ( x ) < 0 , 当 x ∈ ( x1 ,x2 )时 ,f ′ ( x ) > 0.

　　若 a > 1 时 ,当 x < 0 时 ,2lna ·ax  > 0 ,2ex < 0 ,则 此时f ′ ( x ) > 0 ,与前面矛盾.

　　故 a > 1 不符合题意.

　　若 0 < a < 1 时 ,则方程 2lna · ax  - 2ex = 0 的两 个根为 x1 ,x2 , 即方程 lna · ax  = ex 的两个根为 x1 , x2 ,即函数 y = lna · ax  与函数 y = ex 的图象有两个 不同的交点.

　　因为 0 < a < 1 ,所以函数 y = ax  的图象是单调递 减的指数函数.

　　又因为 lna < 0 ,所以 y = lna · ax   的图象由指数 函数 y = ax  向下关于 x 轴作对称变换 ,然后将图象 上的每个点的横坐标保持不变 ,纵坐标伸长或缩短 为原来的 lna 倍得到 ,如图 4 所示.
 

图　4

　　设过原点且与函数 y = g ( x )的图象相切的直线的切点为 (x0 ,lna ·ax0 ) ,则切线的斜率为 g′ ( x0 ) = ln2 a ·ax0 .

　　故切线方程为 y - lna ·ax0  = ln2 a ·ax0 ( x - x0 ). 则有 - lna ·ax0  = - x0  ln2 a ·ax0 .

　　解得 x0  = .
 

　　则切线的斜率为ln2 a ·a= e ln2 a.

　　因为函数 y = lna ·ax  与函数 y = ex 的图象有两 个不同的交点 ,所以 e ln2 a < e ,解得 < a < e.
 

　　又 0 < a < 1 ,所以 < a < 1.
 

　　综上所述 ,a 的范围为（ ,1 .）

　　例 4、例 5、例 6 分别通过构建一种数学函数模 型的形式 ,把复杂问题简单化 ,重点考查学生的数学 建模能力.

　　3 回归数学模型还原

　　数学模式讲究数学问题的属性迁移 ,在数学模 型维度解决 , 回归到认知的问题.

　　例 7    (2022 年新高考Ⅱ卷第 3 题)  图 5 是中 国古代建筑中的举架结构 ,AA′ ,BB′ ,CC′ ,DD′是桁 , 相邻桁的水平距离称为步 ,垂直距离称为举 ,图 6 是 某古 代 建 筑 屋 顶 截 面 的 示 意 图. 其 中 DD1 , CC1 , BB1 ,AA1  是举 , OD1 ,DC1 , CB1 ,BA1  是相等的步 , 相邻桁的举步之比分别为= 0. 5 , =k1 ,  =k2 ,= k3 . 已知 k1 ,k2 ,k3  成公差为 0. 1 的等差数列 ,且直线 OA 的斜率为 0. 725 ,则 k3  = (       ) .

 

图　５　　　　　　图　6

　　A. 0 . 75       B. 0 . 8       C. 0 . 85       D. 0 . 9

　　解析  取 OD1  = DC1  = CB1  = BA1  = 1 ,则 CC1  = k1 ,BB1  = k2 ,AA1  = k3 .

　　依题意 , 有 k3   - 0. 2 = k1 , k3   - 0. 1 = k2 , 且

　　DD1  + CC1  + BB1  + AA1

　　OD1  + DC1  + CB1  + BA1  = 0. 725.

　　所以

　　故 k3  = 0. 9 ,故选 D.

　　例 8    (2022 年北京高考卷第 9 题)已知正三 棱锥 P - ABC 的六条棱长均为 6 ,S 是△ABC 及其内 部的点构成的集合. 设集合 T = {Q ∈S PQ≤5} ,则T 表示的区域的面积为(       ) .

　　A.         B.  π       C. 2π       D.  3π
 

　　解析  如图 7 ,设顶点 P 在底面上的投影为 O ,
　　连接 BO ,则 O 为△ABC 的中心 ,且 BO =  × 6 × = 23 ,故 PO = = 2 6 .
 

图 7

　　因为 PQ = 5 ,故 OQ = 1.

　　故 S 的轨迹为以 O 为圆心 ,1 为半径的圆. 而△ABC 内切圆的圆心为 O ,半径

　　故 S 的轨迹圆在△ABC 内部 ,故其面积为π. 故选 B.

　　例 9   (2022 年北京高考卷第 10 题)在△ABC 中 ,AC = 3 ,BC = 4 , ∠C = 90°. P 为△ABC 所在平面内的动点，1且PC=1，则的取值范围是(    ).

　　A.  [ - 5 ,3]              B.  [ - 3 ,5]  

　　C.  [ - 6 ,4]              D.  [ - 4 ,6]

　　解析  依题意如图 8 建立平面直角坐标系 ,则 C ( 0 ,0 ) ,A ( 3 ,0 ) ,B ( 0 ,4 ).
 

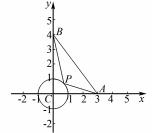
图 8

　　因为 PC = 1 ,所以点 P 在以 C 为圆心 ,1 为半径的圆上运动.

　　设 P ( cosθ ,sinθ ) ,θ ∈ [ 0 ,2π ] ,

　　所以 = ( 3 - cosθ , - sinθ ) ,

　　= ( - cosθ ,4 - sinθ ).

　　所 以 =  ( - cosθ )  ×  ( 3 - cosθ )  + (4 - sinθ ) × ( - sinθ )

　　= cos2 θ - 3cosθ - 4sinθ + sin2 θ

　　= 1 - 3cosθ - 4sinθ

　　= 1 - 5sin ( θ + φ) ,其中 sinφ = ,cosφ = . 因为 - 1≤sin ( θ + φ)≤1 ,
 

　　所以 - 4≤1 - 5sin ( θ + φ)≤6.

　　即 ∈ [ - 4 ,6 ]. 故选 D.

　　例 7、例 8、例 9 分别通过把数学复杂问题回归数 学模型 ,体现出高考命题注重应用性 ,增强试题灵活 性 ,减少死记硬背和机械刷题 ,突出数学建模优势.从以上 2022 年高考题得到数学建模本质 ,需要 广泛知识面、高度开放性和灵活性 ,核心在于利用所 学知识分析问题和解决数学问题的能力 ,进一步培 养学生的数学建模能力.

　　参考文献 :

　　[ 1 ]  中华人民共和国教育部. 普通高中数学课程标 准[M ] . 北京 : 人民教育出版社 ,2018 .