SCI论文(www.lunwensci.com):
摘 要 :在物理学习中 ,经常遇到动态平衡问题 ,物理中的动态平衡问题是指通过控制某些物 理量 ,使物体的状态发生缓慢变化 ,而在这个过程中物体又处于一 系列的平衡状态. 这类问题的特 征是 :“缓慢”移动 ,“缓慢”是指物体的速度极小 ,计算时可以认为速度始终为零 ,也就是说没有加 速度. 因此 , 习题中出现" 缓慢" 移动无论是直线运动还是曲线运动都可以作为动态平衡问题处理. 高中物理中“动态平衡问题”分析是力学重要的知识点 ,也是每年高考的常考点 ,此类问题主要有 “ 一恒一定向”、“ 两变力恒定夹角”、“ 大 Y 模型”三种题型 ,解决此类问题的常规方法有“ 图解法”、 “ 拉密定理”、“ 大 Y 模型”等方法 ,但在争分夺秒的高考考试中这些方法显得那么的“ 不和谐”,本 文把这些方法进行升级理解 ,从而“秒解”动态平衡问题.
关键词 :秒解;动态平衡 ;升级理解;三力平衡;数形结合思想
1“ 一恒一定向”
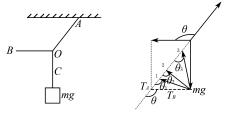
“ 一恒一定向”即为物体所受的三力中有一个 力恒定 ,一个力的方向恒定. 如图 1 所示 , OA、OB、 OC 为三根细绳 ,保持 O 点不动 ,B 绳顺时针旋转 , 分析两绳中的拉力变化情况?
图1 图2
(1) 常规解法— 图解法 ,对 O 点受力分析如图2 所示.
观察图形可知 ,B 绳的拉力先减小后增大 ,A 绳 中的拉力一直减小.
(2) 方法升级理解( 口决 :不转的力随方向变化 的两力的夹角增大而增大 ,减小而减小 ,当方向变化 的两力垂直时转动的力最小 ,往两边都增大)
认真分析可知 , 随着 B 绳顺时针旋转 ,两绳的 夹角减小 , 同时观察 A 绳的力也在减小 , 而当 B 绳 也 A 绳垂直时 ,B 绳中的拉力最小 ,所以可以得到规 律 ,A 绳的拉力( 即不转的力) 随两绳夹角的增大而 增大( 或夹角的减小而减小) ,B 绳的拉力( 转动的力) 在 B 绳也 A绳垂直时最小 ,只要分析 B 绳转动 过程中会不会出现垂直即可判断 ,用此方法则不用 画三角形而快速解决此类问题.
例 1 如图 3 所示 ,把一个光滑圆球放在两块 挡板AB 和 AC 之间 ,AB 与 AC 之间的夹角为 30°. 现 将 AC 板固定 , 而使 AB 板沿顺时针方向缓慢转动90°,则 ( ) .
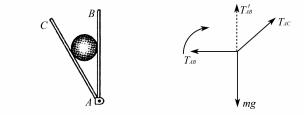
图 3 图 4
A. 球对 AB 板的压力逐渐减小
B. 球对 AB 板的压力先减小后增大
C. 球对AC 板的压力逐渐增大
D. 球对AC 板的压力先减小后增大 解析 画出小球的受力如图 4
由题意可知 TAB 从水平方向转到竖直方向 , TAB 与 TAC夹角一直减小 ,则不转的力 TAC 一直减小 , TAB 在转动过程中一定经历与 TAC 垂直的位置 ,垂直时最小 ,则 TAB先减小后增大 ,故选 B.
2“ 两变力恒定夹角”
“ 两变力恒定夹角”即为两个变力的夹角恒定 , 如图 5 所示,三根细绳连接同一点 O,且在 C 绳上吊 一个重物 ,保持 A、B 绳夹角 α 不变 ,A、B 两绳顺时 针转动30 ° 过程中 ,A、B 绳上的拉力变化情况?
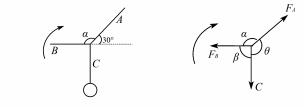
图 5 图 6
(1) 常规解法—“拉密定理”,如图 6
由“拉密定理”可知

由于 G,α 角不变 ,则

不变 ,在转动过程中 β 角从 90°→ 120°,则 sinβ 减小 ,所以 FA 一直减小 , 同 理可知 ,θ 从钝角变到 90°,所以 FB 一直增大.
(2) 方法升级理解( 口决 :“ 对角垂直时拉力最 大”)
由正弦函数知 , sin90° = 1 为最大 ,再由F


可知 , 对角垂直时力最大 , 即当 β = 90°时 ,FA 最大 , 同理 θ = 90°时 ,FB 最大 , 因此处理此类 问题时只要分析两个变化的夹角的变化情况即可得 出结论 ,可以快速的解决问题 ;
例 2 如图 7 所示 , 竖直面内有一 圆环 , 轻绳 OA 的一端 O 固定在此圆环的圆心,另一端 A 拴一 球 ,轻绳 AB 的一端拴球 ,另一端固定在圆环上的 B点. 最初 ,两绳均被拉直 ,夹角为 θ θ > 且 OA 水平 ,现将圆环绕圆心 O 顺时针缓慢转过 90°的过程中( 夹角θ 始终不变),以下说法正确的是( ) .
A. OA 上的张力逐渐增大
B. OA 上的张力先增大后减小
C. AB 上的张力逐渐增大
D. AB 上的张力先增大后减小

图 7 图 8
解 受力分析如图 8
在转动过程中 β 从 90°→ 180° , 由对角垂直时拉力最大可知 ,FAB 一直减小 , 同理 θ 从钝角变成锐 角 ,其间一定经历直角的状态 , 由对角垂直时拉力最
大可知 ,FOA先增大后减小 ,故选 B.
3“ 大 Y 模型”
“ 大 Y 模型”即为晾衣服模型 ,如图 9 所示 ,一 根细绳 A、B 两端分别栓在两根固定的杆上 ,两杆间 的距离为 d ,重物的重力为 G

图 9 图 10
(1) 常规解法:
对 O 点受力分析如图10 所示
由平衡可知
2Tcosα = G
即 T =

由几何关系可知 LOA sinα + LBO sinα = d
其中 LOA + LOB = L绳长得 sinα = Ld绳长
根据题意逐步分析解答.
(2) 方 法 升 级 理 解 ( 口 决:“ 近 小 远 大 , 纵 不 变”)
分析总结规律
①纵移 ,即 A 点或 B 点上、下移动时 , 由于d 不 变 ,绳长不变 ,则 α 不变 ,则绳中拉力不变;
②远离 , 即两杆距离增大 , α 变大 , 绳 中 拉 力 变大;
③靠近 , 即两杆距离减小 , α 变小 , 绳 中 拉 力 变小;
口决:对于 α 和 T 的变化情况满足:“ 近小远大 ,纵不变”,其中“近”和“远”指的是距离 d ,d 小 , α 小 ,绳中拉力小;d 大 , α 大 ,绳中拉力大 ,“ 纵”指 的是 A 点或 B 点上、下移动 ,此时绳中拉力不变.
例 3 (2017 ·天津 ·高考真题) 如图 11 所示 , 轻质不可伸长的晾衣绳两端分别固定在竖直杆 M、 N 上的 a、b 两点 ,悬挂衣服的衣架钩是光滑的 ,挂于 绳上处于静止状态. 如果只改变一个条件 ,当衣架静止时 ,下列说法正确的是 ( ) .
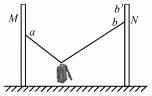
图 11
A. 绳的右端上移到b ′ ,绳子拉力变小
B. 绳的两端高度差越小 ,绳子拉力越大
C. 将杆 N 向右移一些 ,绳子拉力变大
D. 若换挂质量更大的衣服 ,则衣服架悬挂点右移
解 ABC. 利用口决:“ 近小远大 , 纵不变”可 知 ,绳的右端上移到 b′ ,即为纵移 ,则绳子拉力不变 , 将杆 N 向右移一些 ,即远离 ,则绳子拉力变大 ,绳的 两端高度差越小 , 即纵移 ,则绳子拉力不变 ,故 AB 错误 ,C 正确; D. 若换挂质量更大的衣服 , 仍然平 衡 ,则位置不变 ,只是绳子拉力变大 ,故 D 错误.
参考文献 :
[1] 凌旭. 探讨高中物理动态平衡问题的审题和解题技巧[J ] . 启迪与智慧 :教育 ,2018(02) :62 .
[2] 杨温博. 高中物理审题和解题的方法技巧分析 [J ] . 中学生数理化( 学研版) ,2016(8 ) :67 .
[3] 谭欢容. 高中物理力学题解题技巧探讨[J ] . 教 育界 ,2018(34) :62 - 63 .
[4] 郭明飞. 力学动态平衡问题与数学中的圆的不 解之缘[J ] . 物理之友 ,2019 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/47701.html