SCI论文(www.lunwensci.com):
摘 要 :给出2022 年全国高中数学联赛(四川预赛)试题及其解析 ,部分试题给出一题多解 , 解答题给出了有别于参考答案的精彩解法.
关键词 :高中数学联赛;四川赛区;数学竞赛试题;解析
2022 年全国高中数学联赛( 四川预赛)试题 ,全 卷共 11 道题 ,其中 8 道填空题 ,3 道解答题. 命题组 对 8 道填空题 ,只给出了答案 ,没有解析过程 ,3 道 解答题各提供了一种解法供阅卷参考. 笔者对每道 题都进行了分析和研究 ,逐个给出解析 ,解答题还给 出了有别于参考答案的精彩解法 ,供读者参考.
该试题涉及代数运算(第 1 题) ,平面向量(第 2 ,9 题) ,数列(第 3 ,5 ,10 题) ,平面解析几何(第 4 , 9 题) , 函 数 与 数 列 (第 5 题) , 函 数 与 方 程 (第 7 题) ,函数与不等式(第 11 题) ,解三角形(第 6 题) , 立体几何与组合数学(第 8 题).
题 1 已知正实数 a,b 满足 ab = (8a)9b ,则 loga (4a2 ) 的值为—— .
解析 由 ab = (8a)9b ,得 b =9b loga (8a).
所以loga2 = -

.
则loga (4a2 ) =2loga2 +2 =2 × ( -

) +2 =

.
题 2 已知平面向量 a,b 满足 : a = 1 , b = 2 ,a ·b = 1 ,记向量 a + 2b 与 2a - b 的夹角为 θ ,则 cosθ 的值为—— .
解 析 由 a = 1 , b = 2 , a · b = 1 , 得a + 2b = 21 , 2a - b = 2 , (a + 2b) · (2a - b) = - 3.
所以 cosθ =

= -

.
题 3 已知数列{an }满足 :a1 = 1 ,a2 =2 ,a2k + 1 =

,a2k + 2 =2a2k + 1 - a2k (k ∈N ∗ ) ,则 a2022 的末两位数字为—— .
解法 1 由题可得 ak = a2k - 1 a2k + 1 ,2a2k + 1 = a2k + a2k + 2 (k ∈N ∗ ).
又 a1 = 1 ,a2 =2 ,所以 a3 =4 ,a4 = 6 ,a5 = 9 ,a6 =12 ,a7 = 16 ,a8 =20 , …
观察归纳奇数项得 a2k + 1 = (k + 1)2 .
所以 ak = a2k - 1 a2k + 1 = k2 (k + 1)2 .
即 a2k = k(k + 1).
所以 a2022 = 1011 × 1012 = 1023132.
所以 a2022 的末两位数字为 32.
解法 2 由题可得 ak = a2k - 1 a2k + 1 ,2a2k + 1 = a2k + a2k + 2 (k ∈N ∗ ).
又 a1 = 1 ,a2 =2 ,所以 a3 =4 ,a4 = 6 ,a5 = 9 ,a6 =12 ,a7 = 16 ,a8 =20 , …
观察归纳偶数项得 a2k = k(k + 1).
所以 a2022 = 1011 × 1012.
所以 a2022 的末两位数字为 32.
题 4 已知实数 x ,y 满足 x x +

= 1 ,则 3x + y -4 的取值范围为—— .
解析 当 x≥0 ,y≥0 时 ,方程为 x2 +

= 1 ;
当 x >0 ,y <0 时 ,方程为 x2 -

= 1 ;
当 x <0 ,y >0 时 ,方程为

- x2 = 1.
令 3x + y -4 = 2 ·


= 2d,其几何意义为(x ,y)到直线 3x + y -4 = 0 的距离的 2 倍 (如图 1).

图1
联立 x2 +

= 1 和
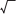
3x+ y + m =0(m <0)得 6x2+2
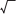
3mx + m2 - 3 =0. 由 Δ =0 得 m = -
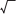
6
又因为双曲线的渐近线为
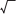
3x+y=0.
所以 d <

=2.
则 3x + y -4 =2d 的取值范围为 [4 - 6 ,4 ). 题 5 已知函数 f: { 1 ,2 , … ,10}→ { 1 ,2 ,5} ,且对一切 k = 1 ,2 , … ,9 ,有 f( k + 1 ) -f( k) ≥3. 则符 合条件的函数个数为 —— .
解析 由 f ( k) ∈ { 1 ,2 , … ,5}且 | f ( k + 1 ) - f( k) | ≥3知f( k) ≠3.
( 问 题 一 般 化 ) 设 函 数 fn : { 1 ,2 , … ,n} → { 1 ,2 , … ,5} ,且f1 ( 1 ) ≠3 ,当 n≥2 时 ,对一切 k = 1 , 2 , … ,n - 1 ,有 f( k + 1 ) -f( k) ≥3.
记函数fn 的个数为 an ,其中满足fn ( n) = 1 或 5 的个数为 bn ,满足fn ( n) = 2 或 4 的个数为 cn ,则 an = bn + cn.
当 n ≥ 2 时 , 对 一 切 k = 1 , 2 , … , n - 1 , 若 fn ( k) = 1 ,则 fn ( k + 1 ) = 4 或 5; 若 fn ( k) = 2 , 则 fn ( k + 1 ) =5; 若 fn ( k) = 4 , 则 fn ( k + 1 ) = 1 ; 若 fn ( k) =5 ,则fn ( k + 1 ) = 1 或 2.
所以 ,当 n≥3 时 ,bn = bn - 1 + cn - 1 ,cn = bn - 1 ,则 bn = an - 1 ,cn = bn - 1 = an - 2 .
故 an = an - 1 + an - 2 .
易得 a1 =4 ,a2 =6 ,递推可得 a10 =288.
题 6 若△ABC 的三边 a,b ,c 满足 a2 + b2 + 3c2 =7 ,则△ABC 面积的最大值为——.
解法 1 (4S)2= ( a + b + c) ( a + b - c) ( a + c - b) ( b + c - a)
= [ ( a + b)2 - c2 ] [c2 - ( a - b)2 ]
= - ( a2 - b2 )2 +2 ( a2 + b2 )c2 - c4
≤2 ( a2 + b2 )c2 - c4
=2 ( 7 - 3c2 )c2 - c4
= -7 ( c2 - 1 )2 +7 ≤7 ,
所以 S≤

当且仅当 c = 1 ,a = b = 2 时等号成立. 所以△ABC 面积的最大值为

.
解法 2 设 AB 边上的高为 h,则

所以 c2 ≤14 -6c2 -4h2 .
即 7c2 +4h2 ≤14.
则 S =

ch =

· 7c ·2h ≤

· ≤

≤

·

=

,当且仅当 h =

,c = 1 ,a = b = 2 时等号成立.
所以 ΔABC 面积的最大值为

.
解法 3 设 AB 边的中点为 D,则
CD2 =

=

.
所以 S =

c ·DC ·sin∠ADC≤

c ·DC
=

c ·

=

·c


当且仅当 c = 1 ,a = b = 2 时等号成立.
所以△ABC 面积的最大值为

.
题 7 函数 f(x)在 (0 , + ∞ )上严格单调递减 , 对任意 x ∈ ( 0 , + ∞ ) ,均有 f(x) ·f[f(x) +

] =

,记 g ( x) =f(x) + 4x2 ,x ∈ ( 0 , + ∞ ) ,则函数g ( x)的最小值为_____ .
解析 以 f ( x) +

代 换 等 式 f ( x) ·f[f(x) +

] =

中 的 x , 得 f [f ( x) +

] ·ff[f(x) +

] +

=

.
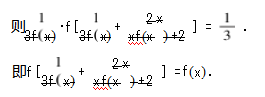
因为 f(x)在 ( 0 , + ∞ )上严格单调递减 ,所以 3fx) + xf(x) +2 = x ,解得 f(x) =

或 f(x) = -

(舍 去). 则 g ( x) =

+ 4x2 =

+

+ 4x2 ≥
3

= 3 ,当且仅当

=4x2 ,即 x =

时等号成立.
所以 g( x)的最小值为 3.
题 8 至少通过一个正方体的 3 条棱中点的平 面个数为 _____ .
解析 12 条棱的中点 ,任选 3 点都不共线 ,可 得 C2 =220 个平面. 其中 4 点共面有 3 +6 + 12 = 21 个 ,6 点共面有 4 个 ,重复的有 21 × (C - 1 ) + 4(C- 1) =21 × 3 +4 × 19 = 139.
所以共有 220 - 139 = 81 个.
题 9 如图 2 所示 ,ABCD 是一个矩形 ,AB = 8 , BC =4 ,M,N 分别是 AB ,CD 的中点 , 以某动直线 l 为折痕将矩形在其下方的部分翻折 ,使每次翻折后 点 M 都落在边 CD 上 ,记为 M′. 过点M′作M′P⊥CD 交直线 l 于点 P ,设点 P 的轨迹是 E.
(1)建立恰当的直角坐标系 ,求曲线 E 的方程;
(2)F 是 MN 上一点 ,FN = - 3 ·FM,过点 F 的直线交曲线 E 于 S,T 两点 ,且 = λ ,求实数 λ的取值范围.
解法 1 (1)以 MN 的中点为原点 O,与 AB 平 行的直线为 x 轴建直角坐标系 ,得 A ( - 4 , - 2 ) , B(4 , -2) ,M(0 , -2) ,N(0 ,2) ,直线 CD 方程为 y =2 PM′ = PM .
所以曲线 E 就是在矩形 ABCD 内以 M为焦点、 CD 为准线、开口向下的一段抛物线 ,所以曲线 E 的 方程是 x2 = - 8y( -4≤x≤4 ).
(2) 由 = - 3 得 F (0 , - 1 ) ,因为点 S,T 在曲线 E 上 ,设 S(4a, - 2a2 ) ,T(4b , - 2b2 ) ,a,b ∈ [ - 1 ,1] ,a≠b ,所以直线 ST 的方程为(a + b)x + 2y -4ab =0.
因为直线 ST过点F(0, - 1) ,所以 a ·b = -

.

因为 a,b ∈ [ - 1 ,1] ,a ·b = -

,
所以 0≤a2 ≤1 且 0≤

≤1. 即

≤2a2 ≤2.
所以 λ 的取值范围是[

,2 ].
解法 2 (命题组提供) (1) 以 M 为原点 ,AB 所 在直线为 x 轴建立直角坐标系. 设 M′(2t,4) , -2≤t≤2 ,则直线MM′的方程为 y =

x ,MM′的中点坐标 为(t,2) ,因为直线 l 是线段 MM′的垂直平分线 ,其 方程为 y -2 = -

( x - t).
将 x =2t 代入上式 ,得 y =2 -

.
所以点 P 的坐标是2t,2 -

.)
故曲线 E 的方程为

(t 为参数) ,消去参数 t,得 y =2 -

.
因此曲线 E 的方程是 y =2 -

( -4≤x≤4).
(2) 因为 = - 3 ,得点 F 的坐标为(0 ,1 ). 设 S(x1 ,y1 ) ,T(x2 ,y2 ) ,则 (x1 ,y1 ) , ( x2 ,y2 )是ìy = kx + 1 ,
方程组

的解.
消元 ,得 x2 + 8kx - 8 =0.①
所以 x1 + x2 = - 8k ,x1x2 = - 8.②
因为方程①在[ -4,4]上有两个不相等的实根 , ì( -4)2 + 8k · ( -4) - 8≥0 ,42 + 8k ·4 - 8≥0

,
î -4 ≤ -4k ≤4 ,
解得 -

≤k ≤

.
由 = λ ,有( - x1 ,1 - y1 ) = λ (x2 ,y2 - 1 ). 所以 x1 = - λx2 .
代入② ,得(1 - λ )x2 = - 8k , - λx = - 8.
消去 x2 ,得 (1 -λλ )2 = 8k2 .
结合 -

≤k ≤

可得 0≤(1 -λλ )2 ≤

. 解得

≤λ ≤2.
题 10 已知正整数数列{an }满足 :对于任意的 正整数 m,k ,都有 am2 = a 及 am2 + k2 = ak am ,求数列 { an }的通项公式.
解析 对任意的正整数 n,都有 an = 1. 下面用数学归纳法证明这一结论.
a1 = a12 = a ,解得 a1 = 1 ;
a2 = a12 + 12 = a1 a1 = 1 ;
a4 = a22 = a = 1 ;
a5 = a22 + 12 = a2 a1 = 1 ;
a3 a4 = a32 +42 = a25 = a = 1 ,则 a3 = 1.
假设结论在 n < k ( k≥6)时均成立 ,下面考查 n = k 的情形 :
(1) 若 k 为 偶 数 ,令 k = 2m ( m≥3 ) , 注 意 到 ( 2m)2 + ( m2 - 1 )2 = ( m2 + 1 )2 .
一方面 ,a(2m)2 + (m2 - 1)2 = a2mam2 - 1 ;
另一方面 a(m2 + 1)2 = m2 + 1 = ( ama1 )2 = a , 于是有 a2mam2 - 1 = a = 1.
从而 a2m = am2 - 1 = 1 ,即 ak = 1.
(2)若 k 为奇数 ,令 k = 2m + 1 ( m≥3 ) ,注意到 ( 2m + 1 )2 + ( m -2 )2 = ( 2m - 1 )2 + ( m +2 )2 .
则 a(2m + 1)2 + (m - 2)2 = a(2m - 1)2 + (m + 2)2 .
所以 a2m + 1 am - 2 = a2m - 1 am + 2 .
因为 am - 2 = a2m - 1 = am + 2 = 1 ,
所以 a2m + 1 = 1 ,即 ak = 1.
由(1) (2)知 ,ak = 1 ,即结论对 k 也成立.
由归纳原理知 ,对任意的正整数 n,都有 an = 1. 所以 ,所求数列的通项公式为 an = 1.
题 11 对任意正实数 a,b,c 及任意正实数 r > 1.

不妨设 a≥b ≥c >0 ,再设
A = (b + c) ·ar - a · (br + cr ) ,
A′ = (b + c) · (br + cr ) ,
B = (c + a) ·br - b · (cr + ar ) ,
B′ = (c + a) · (cr + ar ) ,
C = (a + b) ·cr - c · (ar + br ) ,
C′ = (a + b) · (ar + br ) ,
所以 A + B + C = (b + c - b - c) ·ar + (c + a - c - a) ·br + (a + b - a - b) ·cr =0 ,
A = ab · (ar - 1 - br - 1 ) + ac · (ar - 1 - cr - 1 ) ≥0 , C = -ac ·(ar - 1 -cr - 1 ) -bc ·(br - 1 -cr - 1 ) ≤0,
A + B + C =0 ,A≥0 ,C≤0. ①
即 A′ = (b + c) · (br + cr ) ≤(a + c) · (ar + cr )
= B′≤(a + b) · (ar + br ) = C′.
即 0
据 ① ② , 得 M - N =
 - b
- b  +
+

即 M - N≥0.
所以 b

c +

+ a

b ≤

+

+

,当且仅当 a = b = c >0 时等号成立.
证法 2 设 f(x) =

+

+

,其中 a,b ,c 为正实数 ,x ∈ [0 , + ∞ ). 要证原不等式成 立 ,只需证f(x)在[0 , + ∞ )上单调递增. 因为
(

) ′ =

,

经过计算可得
f ′(x) =

∑ [ (

) ′ + (

) ′]

因此当 r > 1 时有 f(1 ) ≤f(r) ,即原不等式成立 ,当且仅当 a = b = c 时等号成立.
参考文献 :
[1] 中华人民共和国教育部. 普通高中数学课程标 准[M]. 北京 :人民教育出版社 ,2018.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/47637.html
 .
. ) +2 =
) +2 = .
. = -
= -  .
. ,a2k + 2 =2a2k + 1 - a2k (k ∈N ∗ ) ,则 a2022 的末两位数字为—— .
,a2k + 2 =2a2k + 1 - a2k (k ∈N ∗ ) ,则 a2022 的末两位数字为—— . = 1 ,则 3x + y -4 的取值范围为—— .
= 1 ,则 3x + y -4 的取值范围为—— . = 1 ;
= 1 ; = 1 ;
= 1 ; - x2 = 1.
- x2 = 1. = 2d,其几何意义为(x ,y)到直线 3x + y -4 = 0 的距离的 2 倍 (如图 1).
= 2d,其几何意义为(x ,y)到直线 3x + y -4 = 0 的距离的 2 倍 (如图 1).
 = 1 和
= 1 和 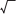 3x+ y + m =0(m <0)得 6x2+2
3x+ y + m =0(m <0)得 6x2+2 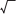 3mx + m2 - 3 =0. 由 Δ =0 得 m = -
3mx + m2 - 3 =0. 由 Δ =0 得 m = - 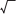 6
6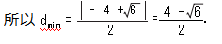
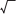 3x+y=0.
3x+y=0. =2.
=2. 当且仅当 c = 1 ,a = b = 2 时等号成立. 所以△ABC 面积的最大值为
当且仅当 c = 1 ,a = b = 2 时等号成立. 所以△ABC 面积的最大值为 .
.