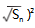SCI论文(www.lunwensci.com):
摘 要 :以培养核心素养为目标的课堂,需要具体的数学方法与思维来提供支撑,而通过有效 问题来设计和驱动课堂教学,则是构建高效课堂的有效途径,引领学生开启思维,解决学生对知识的需 求,让知识自主生成,让数学活动和数学素养进行相互转化,从而真正地发展学生的数学核心素养.
关键词 :核心素养;高效课堂;有效问题
核心素养是人适应信息时代和知识社会的需 要. 数学核心素养包含数学抽象、逻辑推理、数学建 模、数学运算、直观想象、数据分析等六个方面. 那么 聚焦学科核心素养的深度学习,培育数学核心素养 需要什么样的课堂呢? 笔者认为,教师在组织教学 的过程中,抓住学习内容或教学内容的关键特征,通 过有效问题来设计和驱动课堂教学,是培养学生核 心素养,构建高效课堂的有效途径.
下面笔者结合课例《相似三角形中的面积问 题》谈一谈如何让有效问题引领课堂,从而构建核 心素养下的高效课堂教学的尝试.
问题是学习数学的直接驱动力,是数学教学活 动的主心骨,那如何巧妙设问才能让学生质疑,进而 有探究的意愿,又如何让学生在探究问题中激发兴 趣,获得数学知识和基本活动经验,从而锻炼能力,提 升素养,这是我们在课程设计时需重点思考的问题.
1 通过合理创设问题情境引入课题
师 :看到课题中的“相似三角形的面积”,你们 想到了什么?
生 :相似三角形的面积比等于相似比的平方.
师 :请看例 1 :如图 1,AB∥CD,BC∥DE,△ABC 的面积为 1,△CDE 的面积为 4. 你能得到什么结 论吗?

图 1
生 : △ABC 相似于△CDE,相似比为 1 ∶ 2
师 :下面请大家在图 1 上添 1 条或者 2 条线段, 在新图形的基础上,设置一个你能求的关于面积的 问题.
教师先抛出一个非常基本的相似问题,提出添 一条或两条线段,设置一个关于面积的问题. 这个问 题是建立在学生原有的认知基础上,考虑了学生的 最近发展区. 问题的开放型设计,促使学生发散思 维,积极思考,寻找解决问题的方法和途径. 因为是 开放性问题易放难收,容易偏离主题,所以教师在设 置问题时明确了条件“添一条或两条辅助线”并且是“关于面积的问题”,保证问题的有效性.
这个问题从不同层面激发了学生的学习兴趣, 活跃了学生的思维,带动学生快速融入课堂,为后续 的思维活动做好准备.
2 设置变式探究型问题激发深度学习
师 :若上题中△ABC 的面积仍为 1,将△CDE 的 面积改为 2,你还能求上面提出的问题吗?
师 :若将上题中 △ABC 的面积记为 S1,△CDE 的面积记为 S2,你还能求上面提出的问题吗? 生 : (独立思考,小组合作,以小组为单位进行汇报)
学 生 汇 报 结 果 : SAEF = (
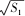
+
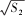
) , S平行四边形BCDF =2

(SΔBCD =

)
例 2 如图 2,AB∥CD,BC∥DE,△ABC 的面积 为 2,△CDE 的面积为 3,你能直接给出△AEF 的面 积,平行四边形 BCDF 和△BCD 的面积吗?

图 2
例 3 如图 3,AB∥CD,BC∥DF,△ABC 的面积 为 4,△CDE 的面积为 16,你能直接给出 △AEF 的 面积,平行四边形 BCDF 和△BCD 的面积吗?
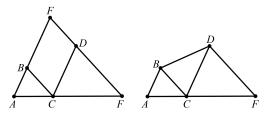
图 3
师 :请大家思考,满足这两个结论的图形,有怎 样的特征呢? 我们是如何解决的呢?
生 :满足三角形的两边分别平行. 找准基本图 形,直接应用结果.
在学生编题的基础上改变三角形面积,由特殊到一般得出面积公式,并初步解决类似问题,在学生 有了充足的活动感悟后提出 :有这两个结论的图形, 有怎样的共同特征呢? 我们是如何解决的呢? 促使 学生思考自己的学习过程和学习策略,这样的反思 与总结,常常是指向数学方法与数学思维的,帮学生 形成关键能力.
例 4 如图 4,正方形 DEFG 为△ABC 的内接正 方形, △ADE 的 面 积 为 1, △EFC 的 面 积 为 1 , △BDG 的面积为 3,则这个正方形的边长为——.
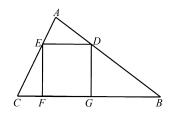
图 4
问 :这个图形与基本图形有什么异同点,可以怎 么转化呢?
例 5 如图 5,在△BCF 中,CF∥DE∥AG,EF∥ AD∥GH,△DEF 的面积为 4,△ADG 的面积为 1,则 图中三个阴影三角形的面积和为——.
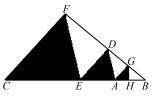
图 5
问 :这个图形中能找出所有的基本图形吗?
例 6 如 图 6,过 △ABC 内 部 一 点 P 分 别 作 △ABC 的 三 边 的 平 行 线 得 三 个 △PDF、△PGH、 △PIE 三角形的面积分别为 1,4,9,则△ABC 的面积 是——.
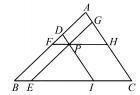
图 6
师 :请同学 们 独 立 思 考,并 尝 试 利 用 多 种 解 法解决.
通过例 4 引导学生利用转化思想变正方形为平 行四边形,例 5 由多个基本图形依次组成,例 6 则由 基本图形叠加而成,思考空间呈螺旋上升,教师的引 导也逐步放手. 例 6 学生给出了三种解法,分别是直 接提炼基本图形,例用相似比转化,例用平移转化为 基本图形.
此时教师调整了原有的设计,在学生给出的解 法上继续提出了问题,进而激发学生继续思考.
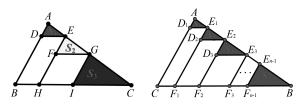
追问 :例 6 同学们给出的如图平移的方法,类比 基本图形的研究过程,根据图 7 及图 8,你们能自添 条件和结论,再编一道新题吗?
生 : △ABC 内小三角形的个数可以变为 4 个,5 个 …甚至是 n 个.
师 :如果把小三角形的面积依次记为 S1,S2 …, Sn,你们会怎么对下面的图形进行探究?
图 7 图 8
生 :我们可以用 S1,S2 …,Sn 表示 △ABC 的面积,也即 SABC = (

+

+ …+
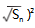
核心素养下的课堂教学,教师要为学生的学而 教,以学定教,以教促学. 每一个数学问题的设计与 探究既要贴近学生的认知需求,还要迎合学生的探 究兴趣,尊重学生的思维活动和思维结果,遵从课堂 的动态生成,把学生真正推向课堂活动的最前沿,充 分挖掘学生的探究潜能,激发学生的自尊与自信. 所 以教师的课堂教学是静态与动态,预设与实施的关 系,引导学生进行学习,让知识自主生成,让数学活 动和数学素养进行相互转化,从而真正地发展学生 的数学核心素养.
3 引导学生发现问题提出问题
在数学的核心素养中,学会发现问题是一项非 常重要的能力,我们的课堂不仅是教师在提出问题, 更应是学生因解决问题继而能提出问题,因为只有学生能够发现问题,才会促进学生更加深入地挖掘 和学习,在解决问题的同时提高自己的数学学习能 力. 在此过程中,教师要注意为学生创造出一种轻松 活跃的氛围,让学生能够真实地表达出自己的想法.
在能力提升 2 的解决过程中,学生不仅给出了 不同的解决方案,还提出了新的问题,如求 5 个三角 形的面积和,求第 n 个三角形面积等问题,同样在创 设问题情境的添线编题中直接连接 BD 的学生,提 出没有平行四边形的面积那该如何直接求出△BCD 的面积,引发同学们的共同思考;深度探究的环节也 都是尝试着让学生不断的提出问题,解决问题,学生 的思维显得非常活跃.
在核心素养的背景下,数学方法和思维能力是 支撑以必备品格与关键能力为基点的核心素养培育 的基础,其涉及的数学抽象,逻辑推理,数学建模,数 学运算,直观想象,数据分析等方面,都需要具体的数学方法与思维来提供支撑. 因此本,节课在经历问题的提出-分析-解决-升华-运用-创新的教学 环节中,教师有意识地引导学生理解运用数学思想 方法, 经历了从特殊到一般的过程,蕴含了类比转化的思想方法和利用基本图形化繁为简,化难为易 的转化思想,开启了学生思维,打造 i 灵动课堂.
裴光亚先生指出 : 如何判断一节课是否成功? 就看它有没有以核心素养为目标的导向,有没有问 题驱动,有没有抽象,推理和建模的架构,有没有激 发学生想象,砥砺品质的生态环境,所以本节课备课 时就是围绕培养学生的核心素养,通过创新问题情 境,引发学生深度思考,让学生去发现问题,提出问 题,分析问题,解决问题,应用问题,创新问题,使其 思,能力得到提升. 以培养核心素养为目标的课堂, 需要教学智慧,需要教师砥砺前行.
参考文献 :
[1] 吕井春. 核心素养背景下初中数学教学设计需 要关注的基本问题[ J ] . 数学教学通讯( 中旬), 2018 (9 ) :54-56 .
[2 ] 张宜兴. 创新问题情境引发深度思考[J ] . 中学 数学教学参考(中旬),2018 (5 ) :9 -11 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/45219.html

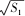 +
+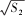 ) , S平行四边形BCDF =2
) , S平行四边形BCDF =2
 )
)




 +
+  + …+
+ …+