 ex-
ex- ,其中a ∈R 且 a ≠0.
,其中a ∈R 且 a ≠0. 时,f(x ) ≥
时,f(x ) ≥ ax (x ≥ -1) .
ax (x ≥ -1) . ,要证明f(x ) ≥
,要证明f(x ) ≥ x,只需证明 1 +x
x,只需证明 1 +x  - ≥
- ≥ x,只需证明 1 +
x,只需证明 1 + x ≥
x ≥ ,此不等式两边平方显然成立.
,此不等式两边平方显然成立. 时,f(x ) ≥
时,f(x ) ≥ ax 等价于
ax 等价于 ex-
ex- ax≥
ax≥ .
. ex -
ex - ax -(ex-
ax -(ex- x ),得 φ′(x ) = ( 1 -a ) (
x ),得 φ′(x ) = ( 1 -a ) (  ex +
ex + ) > 0,φ(x )在[ -1,+∞ )上是单 调递增函数. 所以 φ(x ) ≥φ( -1 ) = ( 1 -a ) (
) > 0,φ(x )在[ -1,+∞ )上是单 调递增函数. 所以 φ(x ) ≥φ( -1 ) = ( 1 -a ) ( -
- ) ≥0,故
) ≥0,故  ex -
ex - ax ≥ ex-
ax ≥ ex- x. 要证明f( x ) ≥
x. 要证明f( x ) ≥  ax,只需证明 ex-
ax,只需证明 ex- x ≥
x ≥  ,此即 a = 1 的情形,已证成立.
,此即 a = 1 的情形,已证成立.
 时,f(x ) ≥
时,f(x ) ≥ ax.
ax. ax 转化为
ax 转化为 -
- ≥
≥ ax,经 过 适 当 代 换,并 结合基本不 等 式,即 可 将 问 题 轻 松 求 解,更 彰 显 了 问题的本质.
ax,经 过 适 当 代 换,并 结合基本不 等 式,即 可 将 问 题 轻 松 求 解,更 彰 显 了 问题的本质. ex ≥
ex ≥ 
 -
- ≥
≥ ax.
ax. =t ( t≥0 ),得 x =t2 -1 .
=t ( t≥0 ),得 x =t2 -1 . -t≥
-t≥ a ( t2 -1 ),
a ( t2 -1 ),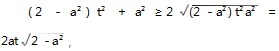

 ≥1 .
≥1 . ≥1 成立.
≥1 成立. 时,f(x ) ≥
时,f(x ) ≥ ax.
ax. ≥1,通过引入正参数 t,将其变形为 2at
≥1,通过引入正参数 t,将其变形为 2at -2at≥0. 进而借助基本不等式 :
-2at≥0. 进而借助基本不等式 : ≤ (2 -a2 ) t2 +a2,可得 2at ≤ (2 -a2 ) t2+a2,即(2 -a2 ) t2-2at+a2 ≥0,亦即
≤ (2 -a2 ) t2 +a2,可得 2at ≤ (2 -a2 ) t2+a2,即(2 -a2 ) t2-2at+a2 ≥0,亦即 -t≥
-t≥ a ( t2 -1 ) . 通过换元,令 t =
a ( t2 -1 ) . 通过换元,令 t = ,则得
,则得 -
- ≥
≥ ax. 最后,借助基本不等式 ex ≥ 1 +x,得到
ax. 最后,借助基本不等式 ex ≥ 1 +x,得到 ex-
ex- ≥
≥ ax,即待证不等式f(x ) ≥
ax,即待证不等式f(x ) ≥ ax.
ax. 及 x.
及 x. ex-b
ex-b +x ≥cx(其中 a >0 ) .
+x ≥cx(其中 a >0 ) .
 -
-  ≥cx.
≥cx. =t,实现第三步所得不等式 形式的进一步简化. 本题得到(1 -ac ) t2 -abt +ac≥0 ( 1 -ac≥0,ac≥0 ) .
=t,实现第三步所得不等式 形式的进一步简化. 本题得到(1 -ac ) t2 -abt +ac≥0 ( 1 -ac≥0,ac≥0 ) .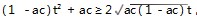 则只需
则只需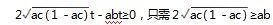 ,只需
,只需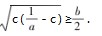
 a,由
a,由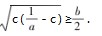 可得a ≤1,此时 c=
可得a ≤1,此时 c= a ≤
a ≤ 符合 1 -ac ≥0,ac ≥0. 从而得到使不等式
符合 1 -ac ≥0,ac ≥0. 从而得到使不等式 -
- ax ≥
ax ≥ 成立的一个充分条件是 0 < a ≤1 .
成立的一个充分条件是 0 < a ≤1 . 及 lnx.
及 lnx. (x +2) -b
(x +2) -b ≥clnx (其中 a,c >0) .
≥clnx (其中 a,c >0) . (x +2) -b
(x +2) -b  ≥c (x -1 ) .
≥c (x -1 ) . =t,得到(1 -ac ) t2 -abt +1 +2ac ≥0(其中 1 -ac ≥0,1 +2ac ≥0) .
=t,得到(1 -ac ) t2 -abt +1 +2ac ≥0(其中 1 -ac ≥0,1 +2ac ≥0) .
 (x +2) -
(x +2) -  ,此时f(x )的函数模型稍显单调,故尝试将
,此时f(x )的函数模型稍显单调,故尝试将 (x +2) -
(x +2) - alnx 进行 组合,令f(x ) =
alnx 进行 组合,令f(x ) = (x +2) -
(x +2) - alnx.
alnx. (2 +x ) -
(2 +x ) - alnx,其中 a ∈R 且 a ≠0.
alnx,其中 a ∈R 且 a ≠0. 时,f(x ) ≥
时,f(x ) ≥ +
+ (x-4).
(x-4). (2x-2) -
(2x-2) - alnx,当 a=2 时,f(x ) = (x -1 ) -lnx,f(x ) ≥0,即 lnx ≤x -1 . 从而可命制如下试题.
alnx,当 a=2 时,f(x ) = (x -1 ) -lnx,f(x ) ≥0,即 lnx ≤x -1 . 从而可命制如下试题. (2x -2) -
(2x -2) - alnx,其中 a ∈R 且 a ≠0.
alnx,其中 a ∈R 且 a ≠0. +
+ (x-4).
(x-4).“产出导向法”是文秋芳教授创建的旨在改进中... 详细>>
如何设计有效的环境治理政策, 是学术界和政策... 详细>>
