挖掘教材习题功能点燃学生思维火花 — 由 一道填空题引发的思考论文

SCI论文（www.lunwensci.com）:
 

　　摘 要 :教材典型例题习题所蕴含的本质规律，有助于学生形成一 个正确的思维方式. 在教学 过程中，教师要对教材例题和习题进行深入的研究分析，探究问题的本质，寻求他的思想来源，寻找 多种解法. 从一题多解或者一题多变中归纳方法，渗透思想，发展学生的思维.

　　关键词 :例题习题教学;问题变式;数感

　　1 缘起

　　教材是知识技能的重要信息载体，往年许多学 生中考试题在教材中都能找到一个影子，而且有一 些题目就是以课本例题、习题为素材改编成的. 因此，教材是平日统考或者中考命题的一个重要依据， 而教材上的例题和习题又具有一定的典型性和代表 性，这就需要教师们在日常教学中，对教材中的例 题、习题进一步地进行归纳、总结，采取“ 一题多解与一题多变”的模式进行教学，举一反三，和学生一起研究总结，同时在数学课堂中培养学生的数感，提高教学的有效性.

 

　　2020 年 1 月份，笔者参加了上海市金山区九年级数学一模调研考试的阅卷工作，负责批改试卷的 第 16 题. 该题目是由沪教版九年级下册第 27 . 5(3)第 30 页第 4 题改编而来. 阅卷后，笔者从教研室获 取了这道题解答情况的相关数据，这道题得分率为 仅为 0. 23.又在自己所教的班级进行了一节试卷讲评课，引发了笔者对解题教学的一些思考.

　　2 习题呈现

       沪教版九年级下册第 27. 5(3)第 30 页第 4 题: 已知相交两圆的半径长分别为 15 和 20.圆心距为 25.求两圆的公共弦的长.

　　2. 1 解法分析

　　解法 1 直接法

　　∵ O1O2 是连心线，AB 是公共弦，(如图 1)，

       
       

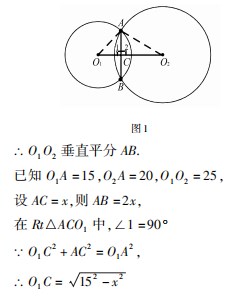
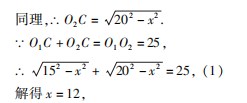
　　∴ AB=2x =24.即两圆的公共弦长为 24.

　　评析 本解法是相交两圆连心线的性质定理的 直接运用. 这是求公共弦常见的一种方法，同学们也 是容易想到的. 但是因为(1)式含有两项无理式，需 要两次平方才能化成整式，所以计算量确实不小.

　　解法 2 间接法(先求圆心距其中的一段)

　　∵ O1 O2 是连心线，AB 是公共弦，(如图 1)，

　　∴ O1 O2 垂直平分 AB，

       

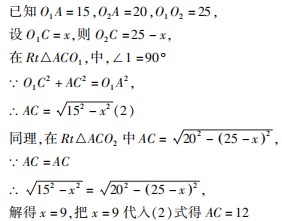
　　∴ AB=2AC=24.即两圆的公共弦长为 24.

　　评析 因为相交两圆的连心线垂直平分公共 弦，所以肯定存在两个直角三角形. 如果把圆心距的 一段设为 x，利用同一个量的两种表示相等列出方 程，求出对应的 x 从而即可求出弦长. 这种间接设元 的方法在数学解题中也是很常见的.

　　解法 3 间接法(面积法)

      

　　∴ AB=2AC=24.即两圆的公共弦长为 24.

　　评析 该解法敏锐地观察到了 15 、20 、25 是一 组勾股数，得到一个直角三角形. 从计算上来看，计 算量也不大，很容易求出结果. 这个解法给我们以后 解题提供了一个很好的思维活动经验，要仔细琢磨.

 

 

      2. 2 变式题组

　　变式 1 已知半径长分别为 6 和 8 的圆 O1 和 圆 O2 相交于 A 、B 两点，且∠O1 AO2 =90 °，求圆心距 AB 的长.

　　变式 2 已知圆 O1 和圆 O2 相交于 A 、B 两点， AB=8.O1 O2 =10.圆 O1 半径为 5.求圆 O2 半径.

　　变式 3 已知圆 O1 和圆 O2 相交于 A 、B 两点， 公共弦 AB =24.大圆 O2 的半径为 15.O1 O2 =4.求 小圆 O1 的半径长.

　　变式 4 已知圆 O1 和圆 O2 相交于 A 、B 两点， 公共弦 AB=24.小圆 O1 的半径为 13.大圆 O2 的半 径为 15.求 O1 O2 的长.

　　本题组的四个变式训练，问题的大背景没有变， 这样我们可以通过节省练习的时间，提高课堂学习 效率. 此外，通过学生对问题的探究可以帮助他们理 解更有难度的问题，用发散思维思考，看透问题的本 质. 变式训练法有利于提高学生的创新意识，使学生 能够独立解决问题，有利于他们未来的成长.

　　3 功能分析

　　3 . 1 有助于巩固新知

　　本习题是学生学习了相交两圆连心线的性质定 理之后设置的. 通过变式题组的练习训练学生的思 维能力，让学生克服自己原有的思维方式，理解新知 识在题目中的应用. 对于大部分学生来说，如果就一 直练基本题目，对于学生的思维能力发展没有多大 的帮助，因此在变式题目中可以适当增加逆向思维 或者新旧知识结合的题目. 通过运用知识，加深学生对 相交两圆连心线的性质定理的理解，巩固新知.

　　3 . 2 有利于归纳数学方法

　　在习题教学时，很多教师采用“就题论题”，只 教“是什么”，很少教“为什么”，更少教“怎么想到的”. 教师在教学中要重视解题指导，要能做到三个 “坚持”:坚持以知识溯源为思路引领，明确思考方 向;坚持以教会学生怎么想为能力抓手，强化学法; 坚持以同一类型还可以怎么做作为拓展方向，力求 以一题会一类. 这样，重点培养学生分析问题和解决 问题的能力，使学生能够轻松地处理新问题.

　　3 . 3 有利于培养学生的数感

　　在上述 2. 2 变式题组的训练中，通过解题活动 会发现常见的勾股数 6 、8 、10;9 、12 、15;15 、20 、25; 5 、12 、13 等. 其实前三组数据和我们熟知的勾股数 3.4.5 是对应成比例的. 在习题的多角度探索中，这 种数感是可以通过反复训练培养出来的. 数感是人 们对数的直接感知能力，数感在数学教学和数学运 算中起着重要的作用. 培养学生数感也是我国当前 数学课堂教学的一个非常重要的任务.

　　3 . 4 有利于数学思维的发展

　　通过这种分层思维训练，有利于培养学生的发 散思维品质，提高课堂质量. 首先，例题、练习教学要 足够重视发散性思维训练，而“ 一 题多解、一 题多 变”有助于学生形成发散性思维. 所以，在解题后教 师尝试着追问“还有没有其他解法?”同时，习题教 学还要重视多种解题方法的本质揭示，只有透彻掌 握方法的本质，才能实现“由会一题到会一类题”的 方法迁移. 例题、习题教学要立足其显性功能的开 发. 其次，教材上的典型习题，很多都具备变式或者 拓展延伸的空间，因此还要学会挖掘其隐性功能. 二 者兼具才不会浪费例题资源的价值，也就不会错过 欣赏习题教学的美丽风景.

　　4 链接一模

　　(2020 年 1 月长宁金山一模 16 题)已知相交两 圆的半径长分别为 8 和 15.圆心距为 17.则这两圆 的公共弦长为 .

　　解题思路 通过对教材 27 . 5(3)第 30 页第 4 题习题的解法研究，本道题通过简单的验算我们很 容易得到 8.15.17 是一组勾股数. 采用上面问题的

　　解法 3.利用面积法，很容易求出公共弦长 . 如果我们不认真琢磨出题人的用意，而是直接采用类似 于解法 1 的方法，那么想把正确答案求出却是有很 大的困难.

　　5 教学反思

　　5 . 1 把教材题目用好些

　　教材的例题和习题是经过众多专家精心遴选、 反复斟酌而定的，是教材的一个有机组成部分. 它在 帮助学生把握双基，完善知识结构，培养和提高思维 能力等各方面起着重要作用. 作为一线教师，更应该 从课本中挖掘例题习题的功能，在对课本习题多角 度探索的过程中，提炼和优化解题方法，为学生遇到 类似的考题能够迅速找到最优方法打下基础.

　　5 . 2 把思维教得灵活些

　　课堂教学中不能贪多，尤其是在解题教学中更 不能贪多. 在学生的难点处，请勿“一带而过”. 在同 学们的思路卡壳时，教师要给他们多一点的思考空 间，用启发性问题引导学生，鼓励他们进行多样化的 尝试探索，寻找解决问题的最佳方法. 在这样的教学 过程中，学生获得的解题经验才深刻.

　　5 . 3 把自己教的善思些

　　通过这一次一个小题目的得分率反思自己的教 学，我们还有很多需要改进的地方. 我们要反思自己 的教学，反思自己的课堂，才能常教常新，学生才能 常学常优. 虽然教学是有遗憾的艺术，但我们应该努力 为学生走向数学学习的“诗和远方”铺设道路.

　　参考文献 :

　　[ 1 ] 谢翔. 挖掘例题美育价值，培养数学核心素养 [J ] . 中学数学教学参考(中旬)，2019 ( 8 ) :55-57 .

　　[2 ] 钱宜锋. 一道教师学科知识竞赛试题的命制与 感悟[J ] . 中学数学教学参考(中旬)，2019 ( 8 ) :58-60 .

　　[3 ] 形成云. 基于发现，历练思维[J ] . 中学数学教 学参考(中旬)，2019 ( 11 ) :27-29 .

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！
 

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jiaoyulunwen/41469.html