SCI论文(www.lunwensci.com):
摘要:数列问题既是归纳推理的重要载体,也在考察演绎推理能力中占有重要的地位.证明数列型不等式,因其思维跨度大、构造性强,需要有较高的放缩技巧而充满思考性和挑战性,能全面而综合地考查学生的潜能与后继学习能力,这类问题的求解策略往往是:通过多角度观察所给数列通项的结构,深入剖析其特征,抓住其规律进行恰当地放缩.
关键词:放缩尺度;项数;待定系数
1教学内容分析
本节安排在数列求和复习结束后,在学生充分了解并掌握数列常见的几种求和方法的前提下,更进一步对数列与不等式的放缩问题进行深入挖掘.教学内容分为三个方面:第一个方面是让学生学会识别不同类的数列放缩,第二个方面是掌握放缩的两大基本要素,第三个方面从构造方面让学生切实掌握有效可操作的方法解决数列放缩问题并领会其思想.
2学情分析
对于刚复习完数列的普通学生来说,对数列的基本知识与方法有了一定熟练度,尤其是求和公式也能熟练应用.但是对于数列不等式放缩,大部分学生都有一定程度的惧怕心理,苦于无方法,难操作,因此思维灵活性受到制约.
3设计思想
本节课采取探究式课堂教学模式,即课前讨论—课上探究—课后总结,在学案启发设计引导下,以学生独立自主和合作交流为前提,以问题为导向设计教学情境,以数列放缩的方法和思想为基本探究内容,让学生通过个人、小组、集体等多种解决问题的尝试活动,在探究学习的过程中把放缩的思想融入到解决问题的方法中.
4教学目标
(1)引导学生从已有的简单放缩问题出发,通过一道数列放缩小题的求解,由特殊到一般地对放缩技巧理解并归纳.
(2)通过对实际问题的探索,培养学生观察问题、分析问题、解决问题的能力,增强学生的协作能力和交流能力,发展学生的创新意识,培养创造性思维的能力.
(3)培养学生合情合理探索数学规律的数学思想方法,通过数列放缩技巧的归纳和整理提升学生逻辑推理与演绎推理的能力.
5教学重点与难点
教学重点:数列放缩的两大基本要素以及放缩的基本思路.
教学难点:放缩技巧的实际应用:转化与计算
6教学过程
6.1回顾数列求和的基本内容以及数列放缩的问题
教师:数列问题难度可分为以下三个层次:通项公式,求和公式都能求解;
通项公式能求解,求和需要放缩;
通项,求和都需要放缩.
6.2例题讨论,分析放缩的两大基本要素
问题一:数列放缩注意哪些点?(带着问题做例1)
例1证明:
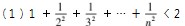 (n∈N∗)
(n∈N∗)
(2)
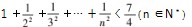
(3)

设计意图:了解学生掌握放缩的程度以及技巧性的能力
学生:讲解方法(让学生讲解放缩的过程)第一类是
第二类是
第三类是
教师:三种不同的放缩方式可以观察出什么特点吗?
学生:一类比一类更加贴近原式的值,也就是放缩的尺度更精准.
教师:若是大部分同学想不到第二类或者第三类的放缩方式,只有第一类放缩的方式容易想到,是否就无法解决2,3两个问题?
设计意图:通过参与学生的讨论,把放缩的项数问题渗透到学生的思想中.
学生:既然放缩的技巧达不到精度,我们可以尝试把放缩的项数减少,前几项用真实值.
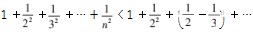

发现只要从第三
项开始放缩,用第一类放缩也可以解决第二类问题.以此类推让学生们尝试用第二类放缩技巧去解决第三类问题.
教师:回顾第一个问题,数列放缩注意哪些点?学生:放缩的技巧以及项数
归纳总结:尺度不够,项数来凑,项不过三,尺度再转
设计意图:学生通过运算对比体会到放缩的技巧和项数同样重要.
6.3探究放缩的技巧与方法
教师:如何有效构造数列放缩?思考有哪些常见的求和式可以与常数比较大小?
学生:裂项相消,等比数列错位相减
问题二:如何构造裂项相消和等比数列才是问题难点,带着这个问题一起来做一下例2.
例2已知数列{an}的首项a1=1,前n项和为
Sn,且an+1=Sn+n+1,n∈N+(1)求证数列{an+1}为等比数列;(2)设数列{ }的前n项和是Tn,求证Tn<
}的前n项和是Tn,求证Tn< (第一小问容易解决an=2n-1,重点分析第二小问)
(第一小问容易解决an=2n-1,重点分析第二小问)
学生:用糖水公式,

让学生尝试运算可以发现,用这个放缩必须要从第四项开始放缩才能解决,且运算量大.
设计意图:学生通过运算体会到放缩的尺度的把握的重要性.
教师:若是把最后的

改成

那放缩更加要往
后推,运算量不言而喻了.回顾刚才方法还是要放缩成等比数列,问题在于这个尺度我们无法把握,所以如何在放缩过程中调整才是关键?
学生:能不能试着用待定系数?目标就是等比数列求和.
师生合作
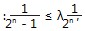
通过计算放缩后的结
果再限定参数λ的范围. 当n=1时不成立,因而作调整.不等式调整为,
当n≥2时,
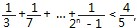
同样的做
法,不等式左边

成立,故
不等式成立.
由此可得:
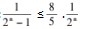
(此类放缩优点在于尺度和项数可以在运算中进行调整,以满足不同程度的放缩)
设计意图:通过师生共同合作体验待定系数可控式的放缩技巧.
教师:前面的问题中提到常见的求和式可以与常数比较大小的除了等比数列的错位相减还有裂项相消,那在这个题目中能实现吗?
学生:裂项关键在于分母因式分解,然后裂项观察相消,无法拼出.
教师:对比之前的例1,同学们可以发现裂项的前后两项是可以通过项与项的关系来放缩的.结合待定系数,我们能不能试用一下?
师生合作:可以对比等比设未知数来裂项,通过代入结果来实现参数的范围求解,对比前面的等比
放缩可得: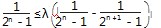
学生参照等比待定系数的过程自行操作,并挑部分学生进行展示.教师提供完整的思路供学生参考.
设计意图:通过实践以及点评让学生体会数列放缩待定系数法的逻辑合理性,消除对于数列放缩技巧性的突兀感.
6.4实践巩固
课堂练习:(2012年广东理)

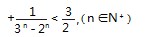
设计意图:通过实践让学生进一步体会两种放缩的技巧的关键.
6.5课堂小结
教师:提示引导学生总结本节课的主要内容学生:思考交流,归纳总结
设计意图:通过学生的总结,培养学生的归纳总结能力和语言表达能力
6.6作业设计
已知Sn为数列{an}的前n项和,a1=2,an>0且2Sn+1-an+1 2=-2Sn其中n∈N+,(1)求{an}的通项公式;
(2)若数列{bn}满足bn=

,Tn是数列{bn}的前n项和,求证Tn<

参考文献:
[1]刘巍.数列的最值问题专题复习教学案例[J].上海中学数学,2013(11):12-14.
[2]胡国兴,谭景宝.例析放缩法在数列敛散性求证中的应用[J].保山学院学报,2019,38
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/40943.html

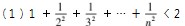 (n∈N∗)
(n∈N∗)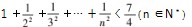

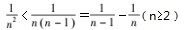

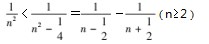
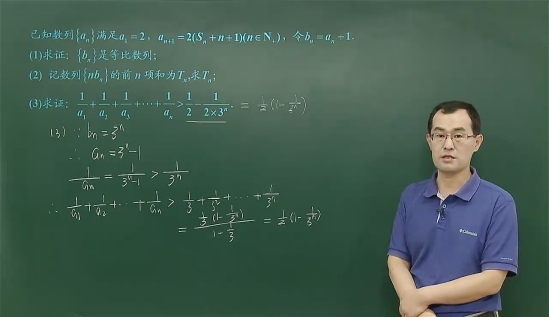
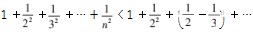
 发现只要从第三项开始放缩,用第一类放缩也可以解决第二类问题.以此类推让学生们尝试用第二类放缩技巧去解决第三类问题.
发现只要从第三项开始放缩,用第一类放缩也可以解决第二类问题.以此类推让学生们尝试用第二类放缩技巧去解决第三类问题. }的前n项和是Tn,求证Tn<
}的前n项和是Tn,求证Tn< (第一小问容易解决an=2n-1,重点分析第二小问)
(第一小问容易解决an=2n-1,重点分析第二小问)
 改成
改成 那放缩更加要往后推,运算量不言而喻了.回顾刚才方法还是要放缩成等比数列,问题在于这个尺度我们无法把握,所以如何在放缩过程中调整才是关键?
那放缩更加要往后推,运算量不言而喻了.回顾刚才方法还是要放缩成等比数列,问题在于这个尺度我们无法把握,所以如何在放缩过程中调整才是关键?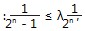 通过计算放缩后的结果再限定参数λ的范围.
通过计算放缩后的结果再限定参数λ的范围.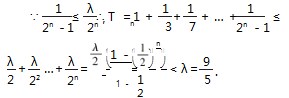

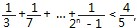 同样的做法,不等式左边
同样的做法,不等式左边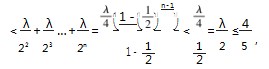
 成立,故不等式成立.
成立,故不等式成立.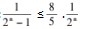
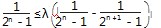

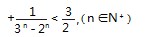
 ,Tn是数列{bn}的前n项和,求证Tn<
,Tn是数列{bn}的前n项和,求证Tn<
