MATLAB软件在大学数学教学中的应用研究论文

SCI论文（www.lunwensci.com）:

摘要：分析了大学数学课程教学中若干知识要点，研究通过MATLAB软件进行有效地、形象化地展示，可以激发学生的学习兴趣，拓展学生视野，使课堂教学生动，从而提高教学质量。

关键词：MATLAB软件；微积分；应用

本文引用格式：顾成扬.MATLAB软件在大学数学教学中的应用研究[J].教育现代化,2019,6(94):164–166.

大学数学已成为我国高等院校绝大多数专业开设的一门必修的课程，其主要内容包括：微积分、空间解析几何、级数和常微分方程等[1]。大学数学课程的特点是高度的抽象性和严密的逻辑性。笔者在多年的大学数学的教学中，深刻体会到，对部分大一新生来说要想学好这门课并非易事，尤其对于财经类、政管类和教育类等偏文科专业学生来说更是如此。近年来，借助计算机软件的多媒体教学已得到了广泛的使用，在大学数学的教学过程中适当运用数学软件，可以对教学内容进行实时处理，借助于图形展示、动画演示等使教学内容更具直观，在很大程度上可降低教与学的难度，缩小数学理论与教学之间的距离，使学生更容易理解与接受，还可以培养学生的学习兴趣，应用数学的能力和创新意识，更重要是节省了保贵的课堂教学时间，从而提高了教学效果。

MATLAB是矩阵实验室（Matrix Laboratory）的简称，是美国MathWorks公司1984年推出的一款数学软件，其主要特点是：高效的数值计算和符号计算功能、完备的图形处理功能、友好的用户界面、自然化的语言和功能丰富的工具箱。大学数学中的各门分支如线性代数、概率统计和常微分方程等课程都可以找到相应的工具箱，使用起来非常方便。在大学数学课堂教学中，借助MATLAB软件的使用，对一些抽象的不易理解的概念和知识点，以图形化方式展示，将数据、推导和演算过程进行可视化，实现复杂问题简单化，抽象内容形象化，可激发学生的学习热情，让学生能更“直观”地学习，深入地领会这些重要的知识点，从而学好这门课程。

一 MATLAB软件在大学数学教学中的一些应用[2-4]

（一）函数极限的可视化

函数极限是研究函数各种性质最基本的功具，也是大学数学中最基本的概念之一。函数极限概念的精确定义即“”定义高度抽象，很多学生理解困难，教学中借助MATLAB软件绘图功能，将无限逼近的过程用动画来演示，可以帮助学生加深理解，还可以记牢一些重要的极限的结果。

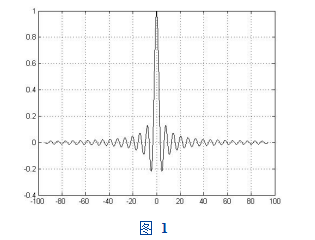
例1作出函数ysin x在[20,20]上的图像，并x判断当x0和x时是否存在极限？

MATLAB程序如下：clear all;clc x=(–30*pi:0.1:30*pi);
y=sin(x)./(x+eps);plot(x,y,'black-');grid on;

运行结果如图1所示，从图像上可以看出，当x0和x时，函数ysin x的取值无限接近常数1和0，x因此它们的极限都存在。


（二）无穷小量阶数的比较

无穷小量就是以零为极限的量，在同一变化过程中，无穷小量趋于零的速度有快有慢，需通过无穷小量阶的比较来确定。当x0时，常见的幂函数无穷小量xn、指数函数无穷小量ex1、对数函数无穷小量ln(1x)和三角函数无穷小量sin x、tan x和1-cos x等，它们趋于零的速度的快慢，在求解微积分很多问题中都有重要的应用。可以在同一坐标系下作出这些无穷小量的图像进行直观比较，让学生更深刻地理解高阶无穷小量以及等价无穷小量等概念。

例2当x0时，比较下列两组无穷小量阶数（1）

x,x3,xsin x（2）x,sin x,ex1,ln(1x)
（1）MATLAB程序如下：clear all;clc x=(–0.5:0.01:0.5);
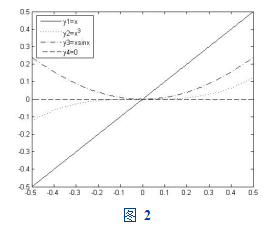
y1=x;y2=x.^3;y3=x.*sin(x);y4=0.*x;
plot(x,y1,'black-',x,y2,'black:',x,y3,'black-.',x,y4,'black--');
legend('y1=x','y2=x^3','y3=xsinx','y4=0',2);

运行结果如图2所示，可以看出当x0时，有xsin xo(x),x3o(xsin x)。


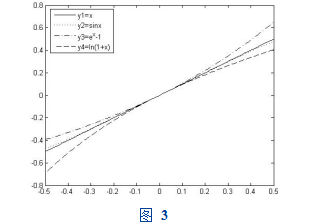
（2）MATLAB程序如下：clear all;clc x=(–0.5:0.01:0.5);y1=x;y2=sin(x);y3=exp(x)–1;y4=log(1+x);plot(x,y1,'black-',x,y2,'black:',x,y3,'black-.',x,y4,'blacklegend('y1=x','y2=sinx','y3=e^x–1','y4=ln(1+x)',2);运行结果如图3所示，可以看出得到当x0时，有 x~sin x~ex -1~ln(x+1) 。

（三）空间解析几何中图形的绘制

用定积分来求图形的面积，体积和弧长时，常常会遇到一些特殊的曲线，例如星形线、双纽线、玫瑰线等。在求解多元函数积分时，也需要了解一些常见的二次曲面的图形，例如椭球面、双曲面和抛物面等。无论是平面曲线图形的还是空间曲面图形，若是手工在黑板上来画，既费时又费事，效果也理想。MATLAB强大的绘图功能就可以完美地画出这些图形来。

例3绘制极坐标曲线a cos(bn)，并了解参数

a,b,n的取值对图形有何影响。MATLAB程序如下：clear all;clc
a=input('a=?')
b=input('b=?')
n=input('n=?')theta=0:0.1:2*pi;rho=a*cos(b+n*theta);polar(theta,rho);

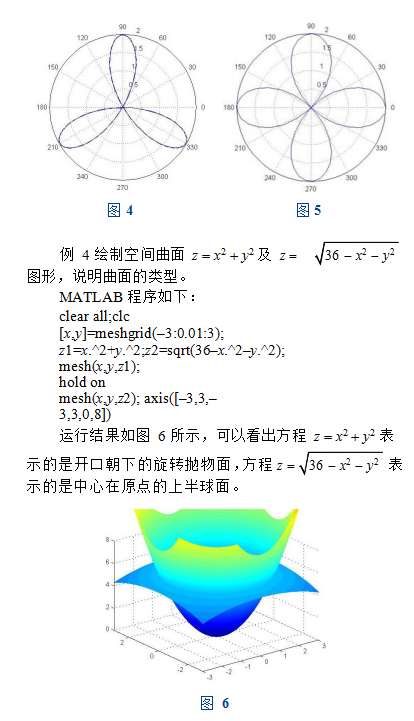
运行程序后，当输入a2,bpi/2,n3，结果如图4所示，函数图形为3叶玫瑰线；当输入a2,b0,n2，结果如图5所示，函数图形为4叶玫瑰线。





（四）泰勒公式与函数逼近

泰勒公式是一个用函数在某点的信息描述其附近取值的公式，因其公式复杂繁琐，学生普遍感到难学。函数泰勒展开式本质上就是用多项式函数来逼近任一函数，通过函数图像可以较好地展示逼近的过程，让学生体会到公式的特点，还可以记牢一些常见函数的泰勒展开式，这比只讲解枯噪无味公式效果会更好。

例5将f(x)sin x中x0处展成泰勒公式，考察函数的逼近过程。



（五）符号计算在微积分中的应用

大学数学中微积分是教学重点，学会求解函数的导数以及各种类型的积分非常重要，在研究函数的性质及其在实际中的各种应用都有重要意义。MATLAB符号计算功能，可轻松解决此类问题。例6研究函数y的单调性和极值。




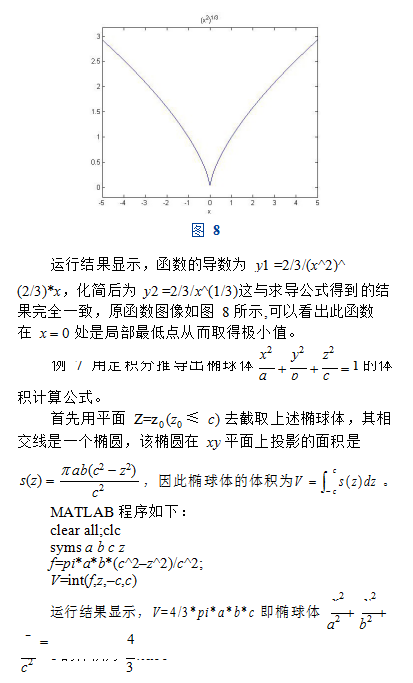二 结语

本文只研究了MATLAB软件在大学数学教学中的部分应用问题，其在线性代数、概率统计和常微分方程等课程中都有非常广泛的应用。总而言之，运用MATLAB软件，结合多媒体教学课件进行大学数学实验性教学，可以让学生在实验过程中更加深刻地理解和掌握大学数学中各种难懂难理解知识要点，激发起学生的学习热情和学习兴趣，并可拓展学生的视野，从而提高教学质量，以适应新世纪培养高素质人才的需要。

参考文献

[1]陈光曙等.大学数学[M].上海:同济大学出版社,2013.
[2]刘卫国.MATLAB程序设计与应用(第二版)[M].北京:高等教育出版社,2006.
[3]张林泉.基于MATLAB的高等数学数据可视化应用研究[J].长春理工大学学报,2010,5(05):182–183.
[4]栾孟杰,张姮妤,崔国范.基于Matlab软件的高等数学教学研究[J].沈阳师范大学学报(自然科学版),2017,35(03):360–363.

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！
文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jiaoyulunwen/30042.html