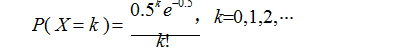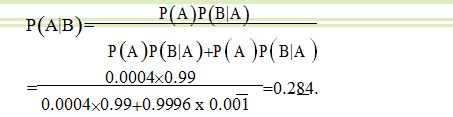SCI论文(www.lunwensci.com):
摘要:概率论课程是应用统计学专业的专业基础课,其应用范围覆盖了医学,社会,经济等各个领域。本文针对医学院校学生的特征,结合医学实际,将理论联系实际,将医学案例引入概率教学,有正对性选择了泊松分布、二项分布、数学期望、贝叶斯公式等4个重要内容,结合医学实际案例,详细分析问题、解决问题,及概率论知识在医学中的实际意义,让学生切实感受到学习概率论知识不是会做几道题,而是能解决身边很多实际问题,实践证明:案例教学法在医学院校的概率论课程教学中对于提高学生的学习兴趣、学生分析问题,解决问题的能力,教师的教学效果具有重要的意义。
关键词:案例教学;医学院校;概率论
本文引用格式:桂梅,等.案例教学在医学院校《概率论》课程中的教学应用[J].教育现代化,2019,6(13):130-132.
在当前大数据时代背景下,统计学专业越来越受青睐,其应用范围几乎覆盖了心理、医学、社会、金融等各个领域。越来越多的医学院校开设统计学专业,如应用统计学,生物统计,这些专业的很多后续课程都是以概率论知识为前提,因此学好概率论是学好其他课程的前提。医学院校统计专业的学生毕业后大多数都从事卫生行政机关、卫生防疫、医药相关部门、疾控中心等工作,在工作中经常会遇到许多临床案例或实际案例,如饮用水中细菌数的概率,患者决策等问题,这些问题的解决都需要依赖于概率统计知识。从医学院校统计学专业的学生角度来看,相对于医学院校的医学专业和其他非医学本科大学统计专业的学生,基础相对更加薄弱,动力不足,由于概率论理论深奥、概念抽象、计算繁杂、难于掌握,学生的积极性不高,学生普遍反映不好理解。因此,如何结合医学院校学生的医学背景特征,将贴近生活或与医学专业相关医学案例引入到概率论的理论教学中,理论联系实际,让学生积极主动思考问题,同时让学生切实感受到学习概率论知识不仅仅是学习抽象的理论知识,而是能解决身边很多实际问题。实践表明:案例教学法在医学院校的概率论课程教学中对于提高学生的学习兴趣、提高学生分析问题、解决问题的能力,以及提高教师的教学效果具有重要的意义[1]。
针对医学院校学生的特点,选取概率论中具有代表性的几个医学案例,引导学生积极思考,自主求解[2],变被动学习为主动学习。
一 泊松分布在生物学中的应用
泊松分布是概率论中一种重要的离散分布,它常用于描述大量试验中稀疏现象(小概率事件)发生的次数的概率分布模型,如细菌、红细胞等在单位面积内计数结果的分布等。
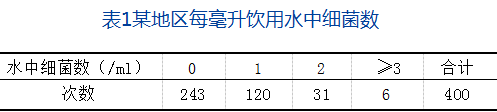
例:为监测某地区饮用水水源的污染情况,现测得该地区400次每毫升饮用水细菌数的数据如下表所示
试计算每毫升饮用水中细菌数的概率及其理论次数,并将频率分布与泊松分布直观比较。[3]
目的:使学生了解泊松分布的实际意义
意义:对概率很小次数较多的随机事件,往往应用泊松分布的理论计算某事件发生的概率,泊松分布中只有一个参数,极大的减少计算的工作量,有很大的实际意义。
解:每毫升水中细菌数发生的概率很小,故可认为每毫升细菌数服从泊松分布。每毫升水中平均细菌数为x0.5,用x代替公式中的,则每毫升水中细菌数的概率分布为:
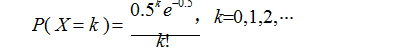
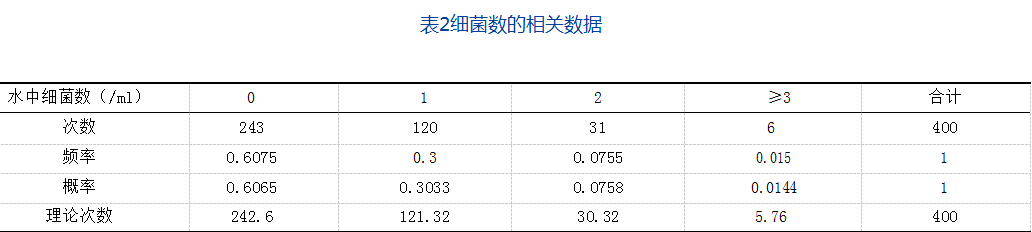
计算结果如表2所示。
由上表可知,每毫升水中细菌数的频率分布与0.5泊松分布是相当一致,由此表明泊松分布应用泊松分布描述单位面积内中的细胞数的分布是合适的。
二二项分布在遗传学中的应用
遗传学中由于基因的随机组合,涉及到不少概率的计算,二项分布模型在计算此类的概率中发挥着重要的作用。
例:人类的白化病是由隐性基因(aa)控制的一种遗传病,一个患者的双亲外观都正常,假设该对夫妇再生4个孩子,求这4个孩子肤色表现型的各种组合[3]。
目的:通过案例讲解,使学生掌握二项分布在计算概率中的应用。
意义:遗传学中很多问题不是有关某一事件出现的概率,有时也涉及到某种事件组合出现的概率[4]。
解:设某一表现型或基因型出现的概率p,另一表现型或基因型出现的概率,满足p+q=1时,根据基因的分离定律,假设患者的双亲都是杂合子(Aa),则在他们的孩子中,不发病的概率是q=3/4,发病的概率为p=1/4,,因此,孩子各种组合的概率就相当于(p+q)4的展开式。
4个孩子都正常的概率为:

由以上结果可以看出,如果患者的双亲都是Aa,则四个孩子至少一个孩子患白血病的概率68.36%,都不患白血病的概率为31.64%。三数学期望在血液化验中的应用期望决策的一个实际应用。
例:某地区居民流行某种传染病,患者约占3%,现对该地区某校5000名师生进行抽血化验,现有两种方案
方案1:逐个化验;
方案2:按5个一组,并将血液混在一块化验,若发现有问题,再逐个化验。
如何判断哪一种方案更好?[5]目的:掌握数学期望的计算。意义:如何利用概率论中的数学期望进行决策。解:方案1:若逐个化验,则共需化验5000次;方案2:设Xi表示第i组的化验次数(i=1,2,···,1000),则Xi服从二项分布,其分布规律如下:

方案2优于方案1,平均而言仅需化验1705次,减少了2/3的工作量。
很显然,该案例中人数越多,患者的概率越小,采用方案2越有效。四贝叶斯公式的应用:患肝癌的概率有多大学习贝叶斯公式不是为了会做几道题,而是知道它的应用(其实学习概率统计中任何理论都是这样)。该公式在现实生活中应用有很多,如下例:
例:甲胎蛋白法诊断肝癌,临床实践表明,已知患有肝癌的人其化验结果99%呈阳性(有病),而没患肝癌的人其化验结果99.9%呈阴性(无病),若将此法用于人口肝癌普查,某地区居民的肝癌发病率为0.0004,现某人的检查结果呈阳性,问他真的患肝癌的概率是多少?[6,7]
解:A={被检查者患有肝癌},B={化验结果呈阳性},由某地区的发病情况可知
若在化验结果呈阳性的情况下,被检查者确实患肝癌的概率多大呢? 由贝叶斯公式得
上式表明,化验结果呈阳性的情况下,被检查者确实患肝癌的概率不到30%,这结果可能会使人感到吃惊,但细想之下就可以理解,因为根据该地区居民的肝癌的发病率可知:10000人中仅有4人患肝癌,9999人不患肝癌,10000人用甲胎蛋白法诊断肝癌,按该法的错检率可知,真患肝癌的4人中化验结果呈阳性的约有40.99=3.96人,不患肝癌的9999人中化验结果呈阳性的约有99990.001=9.996人,即10000人中化验结果呈阳性的仅有13.956人,这呈阳性的人数中仅有3.96人真患肝癌,因此不难理解,化验结果呈阳性中真患肝癌的约占28.4%。
通常进一步提高检验的精度,从而降低错检的概率,然而在实际中由于仪器、技术和操作种种原因,提高检验精度比较困难,常采用的方法是复查,通过复查减少错检率,如在本例中,通过第一次用甲蛋白法检查后,排除了明显不患肝癌的人后,再用甲蛋白法检查被怀疑的对象(第一次化验结果为阳性的人群),此时该人群的肝癌的发病率为28.4%,即PA28.4%,PA71.6%。
从化验结果呈阳性的情况看PB|A0.99,P(B|A)0.001在二次检查呈阳性的情况下,被检查者确实患肝癌的概率又有多大呢?再用贝叶斯公式计算得由上述结果可知:
第一次检查结果呈阳性,被检查者患肝癌的概率为28.4%,首次检查结果呈阳性的人再去复查,复查结果呈阳性的检查者患肝癌的概率为99.7%,这就大大的提高该法的准确了。
五 结束语
针对医学院校学生特征,结合概率论理论实际,将医学案例引入概率的实际教学中,将概率论的教学生活化,融入学生的医学专业背景,引导学生积极主动思考,提高学生的学习兴趣,通过案例与学生一起思考,共同讨论,有助于学生对所学知识点的理解和掌握,让学生切实感受到学习概率论知识不是会做几道题,而是能解决身边很多实际问题,实践证明:案例教学法在医学院校的概率论课程教学中对于提高学生的学习兴趣、教师的教学效果,学生分析问题解决问题的能力具有重要的意义。
参考文献
[1]郭小山.如何在问题解决中培养学生提出问题的能力[J].才智,2014(28):64.
[2]王晓敏,杨莉,黄高明.论医学统计学研究型教学与医学生科研创新能力培养[J].西北医学教育,2014,22(01):121-123.
[3]金明编著.概率论与数理统计实用案例分析[M].北京:中国统计出版社,2014.
[4]李能国.孟德尔遗传实验的教学难点分析[J].中学生物学,2012,28(02):19-20.
[5]高祖新编.医药数理统计方法[M].第6版,北京:人民卫生出版社.
[6]茆诗松,程依明,濮晓龙编著.概率论与数理统计教程[M].北京:高等教育出版社,2011.
[7]龙云翀,王雯,齐勋.数字化校园环境下微课的教学应用策略和效果评估——以医药数理统计课程为例[J].教育现代化,2017(47):196-197.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/7848.html