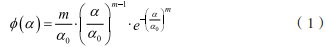SCI论文(www.lunwensci.com):
摘 要:利用岩石破坏过程分析系统(RFPA)对岩石材料的岩石力学实验项目进行了数值模拟,通过数值实验展现了岩石材料裂纹萌生、扩展及贯通的过程及声发射现象,通过数值实验结果绘制了应力 - 应变曲线。把 RFPA 引入岩石力学实验课程教学中,可以弥补教学条件有限的不足,同时也可再现常规岩石力学实验不能观察到的岩石力学现象,从而提高岩石力学实验教学质量。
关键词:岩石力学;数值实验;教学改革
本 文 引 用 格 式: 邬 忠 虎, 唐 摩 天 .RFPA 在 岩 石 力 学 教 学 中 的 应 用 及 教 学 模 式 改 革 [J]. 教 育 现 代化 ,2021,8(40):54-57.
Application of rFPA in rock mechanics Teaching and Teaching mode reform
WU Zhonghu, TANG Motian
(College of Civil Engineering, Guizhou University, Guiyang Guizhou)
Abstract: The numerical simulation of rock mechanics test project of rock material is carried out by using rock failure process analysis system (RFPA). The process of crack initiation, propagation and coalescence and acoustic emission phenomenon are shown through numerical test. The stress-strain curve is drawn through the numerical test results. The introduction of RFPA into the teaching of rock mechanics experiment can make up for the shortage of limited teaching conditions, and reproduce the rock mechanics phenomenon that can not be observed in the conventional rock mechanics experiment, so as to improve the teaching quality of rock mechanics experiment.
Keywords: rock mechanics; numerical experiment; teaching reform
一 引言
RFPA2D(Rock Failure Process Analysis System) 是由东北大学岩石破裂与失稳研究中心开发的岩石破裂全过程分析软件系统。数值计算已被学术界喻为第三种有效的科学研究方法,对于岩石介质而言, 基于破裂过程思想和有限元理论,考虑了岩石介质的非均匀特征来模拟材料破裂过程的非线性特征, 模拟了从细观角度到岩石宏观变形至失稳破坏的全过程 [1-2]。RFPA 在岩石力学及岩土工程领域得到充分应用,使其发生了根本性的发展。
在岩石力学领域学科教学中,岩石力学实验操作和岩石破裂机理作为基本教学内容,是复杂并且关键的 [3-4]。岩石力学是与实际工程紧密相关的,实验教学有利于理论联系于实际 [5]。岩石材料是非连续性及非均匀性的,岩石内部结构与外荷载之间相互影响的复杂性,从教学的角度讲,缺少经济且高效的方法对岩石力学实验进行教学,理论上做好岩石破裂失稳过程详细教学是比较困难的。关于岩石破裂机制的教学研究主要依赖于现场调研及物理力学实验。现场调研对岩石力学学科教学而言是十分必要的,但受到学生数量多,不易管理,教学经费的限制及施工现场的条件不允许,现场调研很难在教学过程中得到充分实现。物理力学实验教学虽然具有直观性,但是对于岩石破裂失稳过程的复杂性很难体现。高校实验室的实验设备很难让学生直观地观察岩石破裂过程,深入了解岩石破裂机理 [6-7]。因此,教师应该基于数值模拟系统平台,辅助验证常规的实验教学,培养学生学会应用 RFPA 软件模拟常规的岩石力学实验,达到教学目的。
二 基本原理及实验流程
RFPA2D 基本原理是将岩石材料离散化为大量细观基元,细观基元力学性质 ( 抗压强度及弹性模量等 ) 的赋值引入 Weibull 统计分布考虑岩石材料的非均质性,建立宏观岩石材料与细观基元之间物理力学性质的联系,引入基元破坏准则和损伤规律作为基元损伤判别依据,利用连续性方法即有限元方法作为应力求解器来模拟材料介质的非均匀性、非连续性。RFPA 基本运算流程为第一步是对模型给定每步位移增量 Δs 进行应力计算,第二步是根据相变准则判断模型中是否产生相变基元。假若不存在新的相变基元,继续增加下一个位移增量 Δs 进行应力计算。假若存在新的相变基元,根据基元的应力状态对基元进行刚度弱化处理并重新进行当前步的应力计算。重复上述过程,直至岩石材料设定的总步数计算完毕 [8]。
RFPA2D 数值模拟教学流程分为三个阶段:
(1)实验准备。数值实验应该在相应的教学准备后进行,学生在数值实验前应该对相关的知识点进行学习,例如岩石材料的选取、岩石材料的基本物理力学参数、加载条件及应变片粘贴位置等,为数值实验建模提供依据。
(2)数值实验过程。依据物理实验的实验结果, 利用 RFPA2D 建立数值模型 , 定义岩石材料物理力学参数和设置边界条件等,对岩石材料破裂失稳过程进行数值模拟,反复模拟调节参数得到与物理实验相似的数值实验结果。
(3)数值实验结果分析。根据 RFPA 数值模拟实验得到试样的应变与应力信息,运用 EXCEL、Origin 等软件绘制图表。此外,根据 RFPA 得到岩石材料裂纹萌生、扩展及贯通过程,以及岩石材料在破裂过程中的声发射分布及大小等实验结果,运用EXCEL、Origin 及 Coreldraw 等软件对如上数值结果整理及绘图,利用 Word 软件编写实验报告。
三 实例分析
利用 RFPA 建立岩石材料数值模型,可以得到岩石力学数值实验的应力应变和声发射 - 步数曲线, 岩石材料在轴向应力作用下破裂过程的应力分布图, 记录轴向应力作用下的试件破裂过程。在教学中, 为了让学生认识岩石材料内部结构与外荷载相互作用导致岩石破裂失稳过程的复杂性,以不同层理倾角页岩试样数值模型破裂失稳过程数值实验为例来说明数值模拟实验的操作步骤及实验结果分析。在力学实验室里,对于岩石抗压强度测定通常是采用室内压裂实验方法,对于岩石破裂过程的记录通常采用高速摄像机拍摄。在物理力学实验过程中,设备数量有限,学生违规操作容易损坏实验仪器,采用数值模拟教学的方法可以解决设备数量有限和实验设备损坏的弊端。学生开展单轴压缩实验、巴西劈裂实验及三轴压缩实验等力学实验时,由于岩石各向异性及非均匀性等因素,很难通过一个岩石试件得到理想的实验结果。并且学生的错误操作导致实验设备的损坏和实验的失败。运用 RFPA 数值模型软件可对岩石内部结构非均匀性等因素对试样应力场分布等的影响进行高效教学,学生运用软件反复演练得到理想的数值结果。
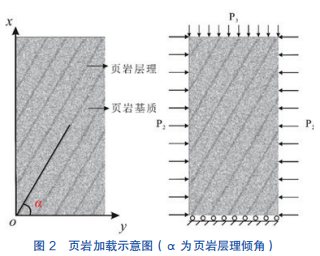
图 1 是不同层理倾角页岩试样的取芯过程及实验室实验设备。从图 1 中可知,通过不同角度的取芯得到不同层理倾角的页岩,取芯过程对设备仪器及人工操作要求较高,在实际操作中很难得到准确的层理倾角,在实际操作中容易出现浪费现象。在物理实验过程中,实验设备的压力室内部具有不可视性,破裂过程很难展现出来。但在 RFPA2D 中, 可以通过设置参数来建立不同的数值模型来模拟岩石材料失稳破裂过程。
图 2 是通过在 RFPA2D 系统中建立的不同层理倾角页岩数值模型加载示意图(α=60°为例),其中颜色较亮的单元是页岩基质,颜色较暗的单元为页岩层理。4 组不同层理倾角的页岩数值模型实际尺寸为 100mm×50mm,其中层理倾角 α 分别为 0°、30 °、60 °和 90 °。将数值模型划分为 200×100 的有限元网格,施加荷载选择双轴压缩,施加围压P2=20MPa,选择加载类型为位移加载,预加载位移初始值为 0.001mm, 单步位移增量 ΔS=0.0003mm, 选择平面应力模型求解,加载过程中记录弹性模量、应力应变、剪应力分布及声发射等数据。
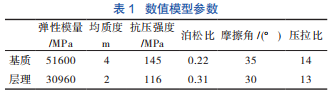
数值模拟过程中页岩基质及页岩层理物理力学参数设置参照文献 [10] 中页岩力学性质,具体参数见表 1。为了考虑岩石的非均匀性,引入 Weibull 统计分布到数值模型材料基元力学特性分布中:
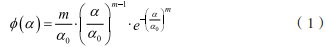
式 (1) 中:α 值表示基元的物理力学参数(抗压强度等);α0 值为基元的物理力学参数的平均值,m 值为均质度,均质度 m 值越大,基元材料力学性质分布越均匀,基元的物理力学参数(抗压强度等) 将集中于一个狭窄的范围之内。
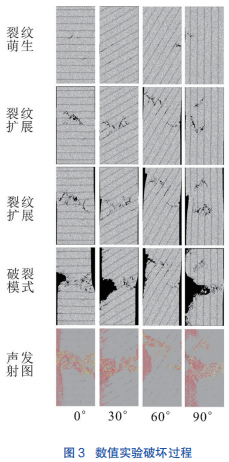
RFPA 是一种通过有限元方法即连续介质力学方法引入 Weibull 统计分布函数模拟非连续介质力学问题的岩石材料破裂过程的新型实验系统,弥补了物理力学实验教学中岩石内部破裂过程可视化的不足。数值实验得到不同层理倾角页岩试样破裂过程如图 2 所示。在图 2 中可知,颜色灰度反映了弹性模量的相对大小,颜色较亮的部位具有较大的弹性模量, 颜色较暗的部位具有较小的弹性模量,裂纹为模型内部的黑色区域。图 2 中可知页岩模型破裂失稳全过程。学生对此破裂过程可以反复观看,在 RFPA 系统中选取具有代表性的裂纹图片,用 Coreldraw 绘制出裂纹萌生、扩展及贯通过程。在物理力学实验中, 很难达到此教学目的。层理倾角 α=0°时,初始裂纹首先在页岩试样中部萌生,然后初始裂纹在层理面间贯通,并且向最大主应力方向即 x 方向延伸形成完整的破裂面,最终发生了岩爆现象。层理倾角α=30°时,初始裂纹首先在层理面上形成,多条裂纹沿层理面方向扩展,最终相互贯通形成宏观裂纹, 最终发生岩爆现象。层理倾角 α=60°时,初始裂纹首先在页岩基质中形成,并向最大主应力方向即 x 方向扩展,与此同时,在页岩左上部形成了新的裂纹并沿着最大主应力方向即 x 方向延伸,形成宏观破裂面,最终发生岩爆现象。在层理倾角 α=90°时, 初始裂纹首先在页岩层理面上形成并向最大主应力方向扩展,形成宏观破裂面,最终发生了岩爆现象。
RFPA2D 软件除了能记录数值实验中页岩试样破裂过程,还可以给出声发射分布。声发射信号是在裂纹萌生和发展的过程中,以弹性波的形式瞬间释放出来的能量。RFPA2D 记录损伤发生的相应步数与声发射空间位置,反映岩石内部的损伤过程,对岩石内部损伤动态演化过程的研究。在教学过程中, 声发射实验设备昂贵,设备数量有限,RFPA 数值模拟系统可以弥补不足,提高教学质量。RFPA 通过声发射颜色区分基元破裂方式(拉伸破坏或剪切破坏),默认红色基元表示当前步数基元发生拉伸破坏, 白色基元表示当前步数基元发生剪切破裂,具体颜色可以自由调换。从声发射图(图 2)可知,不同层理倾角的页岩试样最终破坏模式中,页岩基元大部分发生拉伸破坏,单元颜色表现为红色。小部分单元发生剪切破坏,表现为黄色。即页岩内部以拉伸破坏为主,剪切破坏为辅。
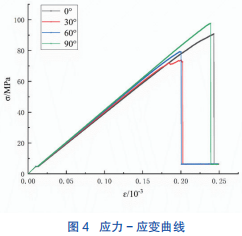
RFPA 计算输入输出数据的单位大部分为国际制单位,长度默认单位为毫米 mm、力默认单位为牛N、应力默认单位为兆帕 MPa。RFPA 计算结束后, 得到各阶段应力、应变值表格,学生运用 origin 制图软件绘制应力 - 应变曲线图,达到加深对岩石应力 - 应变曲线理解的教学目的。图 4 为不同层理倾角 α 下页岩模型应力 - 应变曲线结果,可知随着轴向应变值的增加不同层理倾角 α 下页岩模型应力值依次经历了线性增长阶段、弱化阶段和峰后跌落阶段,最后应力值趋于稳定。值得注意的是,当应力值达到抗压强度后,页岩开始破裂;当应力值最终趋于稳定达到残余强度时,页岩内部裂纹已经贯通。且在应力值达到抗压强度后跌落阶段,各层理倾角页岩试样表现出能量突然释放的特性,应力值大幅度跌落表现出页岩明显的脆性特征。由于页岩内部层理角度的变化,其力学特性表现出明显的各向异性。在层理倾角 α=90°时,页岩试样抗压强度最大;在层理倾角 α=30°时,页岩试样抗压强度最小。不同层理倾角页岩试样残余强度相差不大。
四 结语
在常规的岩石力学实验中,由于实验试件加工的复杂性及实验室条件的限制,实验次数不能太多, 只能做演示实验。因此,RFPA2D 岩石破裂分析系统软件的操作简单和可视化等优点可以引入到高校常规岩石力学教学实验中。在高校常规岩石力学教学实验中,RFPA2D 能够对岩石力学实验教学起辅助教学作用,与常规实验相比,岩石模型受力状态与岩石破裂过程再现功能,可让学生从深层次上认识岩石破坏机理,使得教学实验的效果提升更高的层次,对岩石力学实验教学有着重要意义。
参考文献
[1]黄明利 , 唐春安 , 朱万成 . 岩石破裂过程的数值模拟研究 [J]. 岩石力学与工程学报 ,2000(04):468-471.
[2]朱万成, 唐春安, 杨天鸿, 等. 岩石破裂过程分析用(RFPA~(2D)) 系统的细观单元本构关系及验证 [J]. 岩石力学与工程学报 ,2003(01):24-29.
[3]朱万成 , 唐春安 , 梁正召 , 等 . 应用数值实验方法 , 推进岩石力学实验的教学 [J]. 力学与实践 ,2004(02):76-77.
[4]王述红 , 唐春安 , 朱万成 , 等 . 数值实验在岩石力学实验教学中的应用 [J]. 实验技术与管理 ,2003(06):140-143.
[5]王登科 , 于充 , 左伟芹 .《岩石力学基础》实验教学的改革与探索 [J]. 教育现代化 ,2018,5(19):37-38.
[6]王登科 , 张平 , 姚邦华 . 数值实验在岩石力学基础课教学中的应用与探讨 [J]. 教育现代化 ,2018,5(09):48-50.
[7]李俊玲 , 安玉莲 .“数值分析”课程教学改革的思考与建议 [J]. 教育现代化 ,2019,6(24):62-64.
[8]唐春安 , 赵文 . 岩石破裂全过程分析软件系统 RFPA~(2D)[J]. 岩石力学与工程学报 ,1997(05):109-110.
[9]Yili Lou,Zhonghu Wu,Wenjibin Sun, etc. Study on failure models and fractal characteristics of shale under seepage‐stress coupling[J]. Energy Science & Engineering,2020,8(5).
[10]娄义黎 , 邬忠虎 , 王安礼 , 等 . 流固耦合作用下页岩破裂过程的数值模拟 [J]. 煤田地质与勘探 ,2020,48(01):105-112.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/32437.html