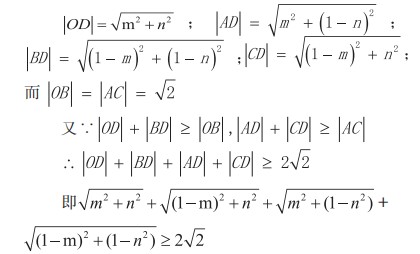SCI论文(www.lunwensci.com):
A Study of Establishing Mathematical Model to Solve Practical Problems in Middle School Mathematics Teaching
PAN Jian, YI You-you, LI Jing, FENG Dan-lu, WANG Di, XIONG Ming-yan
(School of Mathematics and Statistics of Yulin Normal University,Yulin Guangxi)
Abstract: Throughout the ages, mathematics and real life are closely related. Mathematics has been widely used in people’s social life and production. This paper summarizes how to use the mathematical model to solve some practical problems in middle school mathematics, that is, to establish mathematical model to solve geometric problems, algebraic problems and inequality problems. Thus, the abstract and complex problems can be transformed into simple and easy problems.
Key words: Junior high school ;Mathematics model ;Mathematics teaching
一 解决实际问题建模的研究历史
当人类开始使用数字,数学便开始出现。并且随着人类对数字的使用,人们开始建立数学模型, 并利用模型解决生活生产的实际问题。在现代社会生活中,对科技工作者、大学生的综合素质测评、对员工工作业绩的评价及人们的日常活动都可以建立数学模型,并利用该模型解决问题。因此,数学模型是建立问题和数学工具联系的重要桥梁。
在初中数学教学中,解决实际问题是将问题归结为对应的数学问题。通过运用数学概念、方法和理论进行分析研究。数形结合思想是中学解决实际问题的一种重要思想方法,即在研究问题时把数和形结合考虑,把问题的数量关系转化为图像性质, 或把图像性质转化为数量关系,从而把复杂的问题简单化,把抽象的问题具体化。[1] 建立数学模型, 解决实际问题的一个重要思想方法。本文将介绍数形结合思想,并以初中数学教学应用中的数形结合为例进行更详细的描述。
二 建立数学模型应具备的能力
数学模型可以有效地描述自然现象和社会现象 [3], 要想通过建立数学模型解决实际问题,我们必须具有一定的数学解题能力。我们通过分析实际问题, 将实际问题转化为数学问题,并从中建立出一个或多个数学模型,利用数学模型解决数学问题,通过对数学问题的分析来解决实际问题,达到解决实际问题的目的。以上全过程的关键是如何建立数学模型。而建立数学模型能力的强弱将会直接关系到该题的解题方法、速度、质量和结果,同时这也能充分体现出一个解题者的综合能力。
首先,第一步也是极其重要的一步——审题。对题目的了解和理解对之后的建立模型和解决问题起着至关重要的作用。对题目的阅读要求要能充分理解题意,并适当进行分析。其次,建立数学模型解决实际问题的重中之重就是建立数学模型。要想建立一个合适的数学模型,我们就需要对数学模型有充分了解。数学模型有各种各样的模(如:微分方程模型、代数模型、图论模型、随机模型等),我们需要对每一个模型都有所掌握,那么我们才能在建立模型时找到最合适最方便的一个模型。当然, 在建立好数学模型后,对数学模型进行分析计算也是至关重要的。这就主要考验我们的计算解题能力了。因此,计算解题能力也是必不可缺的。在我们的建立数学模型解决实际问题的过程中,也少不了我们每个人单独思考问题的能力。这时,独立思考能力极为重要。以上都是我们在建立数学模型解决实际问题时应具备的能力。
三 建立数学模型解决实际问题的例题分析
我们例举了以下例题,分别是以建立几何模型、代数模型,尤其是运用数形结合思想来求解问题。通过对问题的分析,建立一个最合适题意的数学模型,通过对数学模型的解答进而解决实际问题。
(一) 几何案例
例 1. 如图 1, 已知圆 O 为△ ABC 的外接圆, O 为圆心, 在△ ABC 中,AD 垂直于 BC,BE 垂直于 AC, 且 AD,BE 交于点 H,OG 垂直于 BC 并交BC 与点 G。试证明:AH=2OG。
问题分析与建立模型:本题综合性较强,在圆中糅合了三角形,平行四边形两类特殊的图形,综合考察了圆的性质,三角形中位线,三角形的性质, 平行四边形的判定以及平行四边形的性质等知识点, 题目综合性较强,如何做辅助线构造出新的数学模型来把难的问题简单化是解决本体的关键。本体分别从两种构造模型方法入手,应用平行四边形,三角形知识解决问题,充分体现了建立数学模型在几何应用方面的重要性。
证明:
如图 2 所示,过点 O 做直径 CE 交圆 O 与点 E, 连接 EB,AE,则∠ CAE=90°
即 AE 垂直于 AC,又 BH 垂直于 AC
∴ EA ∥ BH,同理可得 EB ∥ AH
∴四边形 AEBH 为平行四边形
∴ AH=EB
在 Rt △ CEB 中 ,OG ∥ EB,OC=OE
∴ OG 是△ BCE 的中位线,OG=EB 又 AH=EB
∴ OG=AH,即 AH=2OG
结合以上例 1 的分析与证明过程及教学中几何知识的分析,中学几何知识具有立体新颖,抽象, 变化多端等特点,是学生学习中学数学知识的难点之一。但一旦学生对必备数学模型(如三角形,平行四边形以及圆等)的性质有了清晰透彻的了解后, 通过构建这些简单的数学模型很快便能将抽象的问题简单化,进而解决问题。可以说,模型的构建决定了解决几何问题的速度和效率。因此,建立数学模型对于解决中学几何问题具有重大的意义。
即△ ABC 的形状为等边三角形。
分析:若是直接根据已知的公式,我们会发现非常难着手去计算三角形边角之间的关系,因此把几何问题转化成代数问题求解,凑出一个完全平方公式。
(二) 代数案例
例 3. 解不等式 。
问题分析与建立模型:此类不等式题目用到“数轴穿根法”,将代数式转化成更直观的图形计算,有助于学生将头脑中的信息加以形象显示和验证,并通过主动积极的观察、分析和探索活动,加深对解不等式类型题的了解和掌握,发展思维能力,培养创新意识。
解:
一边是因式乘积,一边是零的形式,其中各因式未知数的系数为正。
中学生在对函数的理解上还不是很明白,引入数形结合的方法学生更易接受,直观和形象的优点更加突显出来。
通过以上例题及中学教学中出现的数形结合问题的分析,数形结合是数学解题中常用的思想方法, 数形结合的思想可以使某些抽象的实际数学问题直观化、生动化,能够变抽象思维为形象思维,有助于把握数学问题的本质。数形结合不仅是数学学习中一种重要的解题方法,更是一种重要的数学思想, 相较于传统的解题方法,利用数形结合建立数学模型能更容易解决函数的奇偶性问题,不等式等数学问题。
(三) 不等式案例
一个问题的本质与这个问题之间存在着多种联系,而化归与转化思想便是对这类联系加以总结、概括,并用数学式子对其进行相互转化。在解决一个问题时,可以通过灵活变通,选择最简便的解题方式进行求解。在转化与化归的过程中运用到的方式是多种多样的,例如:图形转化、方程之间的转化、代数与几何的转化、特殊与一般的转化等,有时一个问题可以通过进行多种转化得到同一个答案,体现了其多样性特征。
问题分析与建立模型:在求证条件不等式时, 可以根据题目设定的条件做出对应的图形,然后运用图形的几何性质或者平面几何的定理、公理去建立相应不等式模型,使结论成立。
证明: 建立直角坐标系 , 构造单位正方形, 四顶点分别是 O(0,0),A(0,1),B(1,1),C(1,0), 在正方形内取一点 D(m,n), 连接 OD,AD,BD, CD。
由题可知,其中当 D 取对角线交点是等号成立。
通过以上这个典型例题,数形结合在中学的函数、集合、不等式线性规划、向量等中学教材内容中都有着典型应用。学生通过利用数形结合思想去建立数学模型,使复杂问题简单化、抽象化并具体化。几何问题可以抽象成代数式子,代数问题可用生动、直观的图像表示出来,二者相辅相成,加深学生对题目的理解,从而提高学生的解题效率,培养了学生的创新思维和发散思维。
四 建立数学模型解决实际问题的重要意义
通过对以上经典案例分析与对本问题的解题思路与方法的分析可以了解到,建立数学模型解决实际问题的意义重大。
数学建模思想在中学数学研究领域受到日益重视,国内外许多专家学者对中学数学建模也进行了探讨研究,如吕春兰在《浅谈中学数学建模教学与创新能力培养》中提到学生深入参与建立数学模型的过程中不仅可以培养发散思维和创新能力,并且在求解过程中可以体会到一题多解的乐趣,进一步提高对数学知识的兴趣 [4];司彩琪在《数学建模思想在中学数学中的渗透》一文中明确指出,传统的数学知识的学习与应用过程中已潜移默化的渗透了数学思想,并且建立数学模型解决实际问题己经成为现如今数学教学以及数学学习的趋势 [5];李大潜院士在《将数学建模思想融入数学类主干课程》提出将数学建模思想融入数学类主干课程的教学是有充足根据的等主要研究 [6]。因此,对中学数学建模教学进行讨论探究,具有较大的现实意义和重要价值。
中学阶段是学生成长的关键时期,也是启发培养学生数学思维的最好时机,而构建数学模型解决实际问题是中学阶段学生需要学习并掌握的一项重要技能 . 在中学数学中,利用数学建模来解决实际问题通常是最简洁而又直观的,同时它也是开展数学素质教育的重中之重。在中学教学中引导学生针对要解决的实际问题来构造形象直观的数学模型,再通过对数学模型的研究去解决实际问题,帮助学生形成问题解决策略 , 获得问题解决的基本活动经验, 对培养学生应用数学的意识,提高数学素养与科学思维品质,培养其实践能力和创新能力具有重要作用。所以,在解题教学中重视数学模型方法,不仅能激发学生的学习动机,对培养学生的创新能力和实际能力也是具有重要意义的。
参考文献
[1]曹一鸣 . 数学教学论 [M]. 北京:高等教育出版社,2008.
[2]翁凯庆 . 数学教育学教程 [M]. 成都:四川大学出版社,2002.
[3]钱良均 , 叶春燕 . 初中数学建模有效教学策略研究——以初中数学建模案例展示及分析为例 [J]. 数学学习与研究 ,2019(13).
[4]吕春兰 . 浅谈中学数学建模教学与创新能力培养 [J]. 课程教育研究,2018(18).
[5]司彩琪 ; 数学建模思想在中学数学中的渗透 [N]. 山西省忻州市第七中学发展导报 ,2016.
[6]李大潜 . 将数学建模思想融入数学类主干课程 [J]. 中国大学教学,2006(1).
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/31874.html