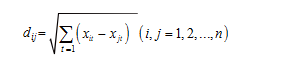SCI论文(www.lunwensci.com):
摘要:近年来,随着高校的不断扩招,伴随而来的学生素质和层次问题引起关注,如果学生层次不一,对教师的教学也是一项挑战。对此本文主要针对不同层次的学生,根据系统聚类方法中的最短距离法,借用MATLAB软件对学生成绩进行聚类,提供适合的教学方法,从而激发学生的学习兴趣,提高教学质量。
关键词:聚类分析;高数成绩;数据挖掘;最短距离法
本文引用格式:段琪.聚类分析在学生高数成绩中的应用[J].教育现代化,2019,6(67):125-126.
随着高校的不断扩招,学生的层次也有很大的差距,对教师而言,用一个统一的标准去教学显然教学效果不会特别理想,对学生的素质提高也起不到良好的效果。此外在文理分科这一块,高中的文科数学介绍的相对简单些,理科数学在难度上相对于文科会有所提升,而大学的很多专业都是文理适用,因此出现学生质量参差不齐的现象也是一种普遍现象[1]。
本次针对汽车学院18级专科学生高等数学平时成绩、期中成绩和期末成绩进行统计,并结合学生具体情况给出合理建议。
一 学生成绩的聚类分析
聚类分析是研究数据的分布情况,将数据划分成多个类,通过观察每个类的共性,从而对数据进行评估和分析,把关系密切的数据归为一类,抽取出自己所需的信息,是一种无监督的学习。聚类分析包含的方法很多,主要有系统聚类法、动态聚类法、最优分割法、图论聚类法等诸多方法[2]。
本文采用系统聚类的方法,系统聚类是聚类分析中较为广泛的一种方法,其基本原理是将一定数量的样本看成一类,然后根据样本的亲疏程度进行聚类,将亲疏程度较高的两类合并,再考虑合并的类与其他类之间的亲疏程度进行合并,重复此过程,直到所有的样本合并为一类。
衡量样本间的亲疏程度通常用到距离与相似系数,本次在欧氏距离的基础上采用最短距离法,而距离是将每个样本看成n个变量对应的m维空间中的一点,根据该空间所定义的距离,距离越近亲密程度越高[3]。
其中欧氏距离公式如下:
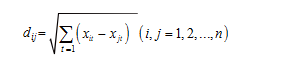
在欧氏距离的基础上,用到最短距离法,该算法将两个类之间的距离定义为一个类的所有个体与另一个类的所有个体之间距离的最小者,用公式表示为:
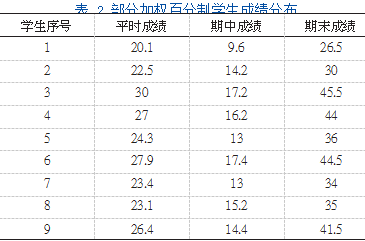
基于对学生进行评估时,平时成绩、期中成绩和期末成绩均按百分制,意味着三者权重相同,但在课堂学习中如果采用:总成绩=30%平时成绩+20%期中成绩+50%期末成绩,对学生进行评估,注重学生课堂表现与应试教育相结合,会显得更加合理[4],见表2、图1。
按照最短距离法,借用MATLAB对其进行评估,结合图1可知,如果将学生分为两类,可分为(1),(2,3,4,5,6,7,8,9),结合学生的具体情况对其进行因材施教,但如果分为两类很显然不是很合理,结合学生具体情况,将其分为三类比较合适,即(1),(2,5,7,8),(3,4,6,9)。
其中(3,4,6,9)整体表现比较稳定,相对比较优秀,在教学过程中可适当加大难度,更好地发挥起特长;(2,5,7,8)这一学生群体基础相似,可根据学生特长适当引导,激发其学习兴趣,提倡自主学习;(1)可能是基础相对薄弱的群体,在教学过程中发现这一学生群体可能是大学之前就对自己没有信心,或者说严重偏科提不起兴趣,导致对数学的学习厌倦,结合学生的具体情况,适当补充初高中的数学知识,与大学知识相结合,让学生重新认识自己,激发学习热情[5]。
二 结语
高校的扩招使得学生群体素质各有差异,从而对教师教学带来难度。聚类分析是数据挖掘中一项重要的技术,已广泛应用于各项领域,根据数据挖掘中系统聚类方法中最短距离法,对学生成绩进行聚类分析,能够更客观合理反映学生的学习情况,根据学生的具体情况因材施教,指导教师的教学工作,提高学生学习的兴趣。
参考文献
[1][美]Pang-NingTan等.数据挖掘导论[M].人民邮电出版社,2006.
[2]张平,等.MATLAB基础与应用简明教程[M].北京航空航天大学出版社,2003.
[3]冯学军,等.聚类分析及相关分析在卓越班学生管理中的应用[J].统计与管理,2014(11):40-41.
[4]柴伟文,等.基于数字特征的高等数学考试成绩的方差分析模型[J].教育现代化,2018,5(14):190-193+245.
[5]朱博顺,程志君,罗玉文,等.MOOC学习者行为大数据的聚类分析[J].教育现代化,2018,5(09):148-150+153.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/27806.html