SCI论文(www.lunwensci.com):
摘要:为了更好地对大学生综合素质进行测评,文章首先概述了主成分聚类分析法,然后分析了大学生综合素质测评现状,最后论述了主成分聚类分析法在大学生综合素质测评中的应用。
关键词:综合素质测评;主成分聚类分析法;大学生
大学生综合素质测评是学生管理工作的一项重要内容,主要涉及德育测评、智育测评、体育测评和能力测评四个方面。从根本上来讲,对大学生综合素质进行测评,不仅能够为评优评奖及就业推荐等提供可靠的依据,还能够全面贯彻落实党的教育方针,促进大学生德、智、体、能全面发展。鉴于大学生综合素质测评是一项十分细致复杂的行政管理工作,又涉及思想教育工作,所以有必要探究具体的测评办法。以下将对主成分聚类分析法在大学生综合素质测评中的应用加以探讨。
一、主成分聚类分析法概述
(一)主成分聚类分析法简介
主成分聚类分析法是主成分分析法、聚类分析法的有效结合,该方法在应用时首先会对数据的主成分进行系统、全面的分析,将原来指标进行整合,使其成为一组更加完善的综合指标,并按照大学生综合测评需求,从其中挑选出对应的指标,构建主成分得分矩阵,更好地反映与展示原指标包含的信息量,然后再利用聚类分析对通过主成分得分数据与原始数据计算出的矩阵进行数理统计与聚类分析,明确各样本间的亲属关系,在对其类型进行客观划分的同时,获取主成分聚类排名。简而言之,主成分聚类分析是将两种分析方式有效结合的一种综合测评方式,即先进行主成分分析,选出其中数项主成分,然后对选出的样本实施聚类分析,最后得到对应的测评结果。
(二)主成分聚类分析法应用步骤
第一,收集n个检测样本,所有的检测样本均包括p个检测指标,由此可得到对应的数据矩阵X=(xij)n×p。为消除量纲与数量级带来的影响,对数据实施标准化处理,设标准化之后的矩阵为Y=(yij)n×p,其中yij=(xij-xj)/sj,xj

是第j列的平均值,

是第j列的标准差。标准化处理不改变各个指标间原本的相关系数。
第二,计算样本相关系数矩阵

。
第三,求出相关系数矩阵R的特征值λ1≥λ2≥…≥λp>0,以及对应正交化单位特征向量ti=(t1i,t2i,…,tpi)T,i=1,2,…,p。
第四,确定主成分个数。方差贡献率体现了主成分包含的信息量大小,根据主成分的累计方差贡献率,确定取r个主成分(即前r个主成分的累计方差贡献率超过85%),获取主成分综合得分F=η1F1+η2F2+…+ηrFr,ηr是各个主成分的方差贡献率。
第五,计算n个样本在以上r个主成分上的得分,并按照主成分得分对各个样本进行排序。
第六,整合各个主成分各阶段的得分数据,并对所有样本进行聚类分析,得到综合主成分得分,再明确所有样本的排序,最后对其实施综合评价。
二、大学生综合素质测评现状
大学生综合素质测评是对学生在校表现和各方面素质的测定和评价,是学生全面发展的导向目标,也是对学生进行教育和管理的重要环节之一[1]。即通过收集、整理大学生学习、生活、实习等过程中能反映其综合素质的表征信息,对表征信息的价值、量值进行判断与综合评定。针对大学生综合素质进行科学的测评,能够对大学生形成一定的教育约束作用及正确的教育导向作用,从而有机整合大学教育进程中的“教”与“学”,让大学生在提升其专业学习成绩的同时,重视其他技能、素质的齐头并进,进而实现自身综合素养的提升。
目前,大学生综合素质测评已经逐步发展为大学生评优及企业选择大学毕业生的核心依据。高校在对学生的综合素质进行评价时,传统的做法是从现有的指标中精选若干个有代表性的指标,但人为地精选指标难免带有主观随意性,可能丢失部分有价值的原始信息。因此,选择适宜的测评方式,实现对大学生更加科学、客观的综合测评已势在必行,这直接关系着大学生的长远发展,对此,有学者提出了几种常用的测评方法[2-4]。
评价学生的综合素质属于多指标(变量)问题。在很多情况下,不同的指标之间具有一定的相关性。由于指标较多且指标之间有一定的相关性,这就增加了分析问题的复杂性,而人们常用主成分分析法评价多指标问题。主成分分析法是一种通过降维技术,将原来具有一定相关性的多个指标转化为互相无关的综合指标的统计方法[5]。综合指标是原始变量的线性组合,能够反映原始变量的绝大部分信息。比较常用的方法是:当第一主成分F1的方差贡献率较高(一般在85%以上)时,可以认为该主成分能反映的信息与原始变量包含的信息差不多,此时可以按第一主成分的得分进行排序评估。若第一主成分F1的方差贡献率不够高,可考虑多个主成分F1,F2,…,Fr,再以各个主成分的方差贡献率为权重,构造主成分的综合得分,最后利用样本的主成分综合得分进行排序和综合评价。
然而由第一主成分定义可知,第一主成分F1是所有原始变量线性组合中的方差最大者,综合得分F表示为原始变量的线性组合,因此综合得分F的方差小于第一主成分F1的方差,也就是说主成分综合得分并没有提高信息含量[6]。用这种方法对学生进行评价,不能很好地反映实际情况。针对该种状况,为寻找更合理的评价方案,可引入一种更加客观、有效的测评方式——主成分聚类分析法,该方法集合了主成分分析法与聚类分析法的优势,能够实现对大学生更加全面的测评,进而根据测评结果为其提供有针对性的教育服务,促进其长远发展。
从实际的运行结果来看,应用主成分聚类分析法对高校学生的综合素质进行评价总体上是合理的,这能为大学生创造一个相对公平的育人环境,因此是有积极意义的。
三、主成分聚类分析法在大学生综合素质测评中的应用
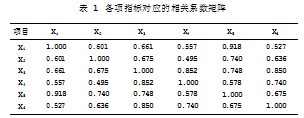
本研究以闽南理工学院土木工程学院2020级给排水工程1班为例,选取该班20名学生作为综合素质测评对象,通过调查研究、论证,选取反映大学生当前发展现状与综合素质的六项指标进行综合测评,包括整体学习成绩(X1)、政治教育水平(X2)、道德素养(X3)、宿舍执勤情况(X4)、自学情况(X5)、实践中的综合表现(X6),以该六项指标为基础,得到一个20×6的原始数据矩阵,利用SPSS 22.0软件对原始数据实施标准化处理[7],计算得到相关系数矩阵R,如表1所示。
综合分析表1,可发现大学生整体学习成绩(X1)与其自学情况(X5)有较大的相关性,道德素养(X3)与宿舍执勤情况(X4)存在较大的关联。
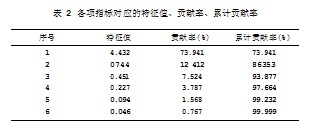
根据各个主成分之间的关系,计算相关系数矩阵R的特征值、贡献率与累计贡献率,如表2所示。
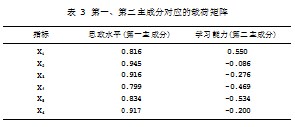
由表2可知,最大的两个特征值分别4.432和0.744,对应的方差贡献率分别为73.941%和12.412%,第一特征值的贡献率没有达到85%,因此选取前两个特征值,其累计贡献率为86.353%,这意味着在新的指标体系中这两个指标就可以反应样本差异的86.353%,能够概括各指标的大部分信息,故而提取这两项主成分构建载荷矩阵,如表3所示。
由表3可以发现,第一主成分变量前载荷系数均大于0.8,能够综合反映学生各方面的素质,而学生的政治教育水平、道德素养、实践中的综合表现等皆存在较大载荷系数,表明第一主成分可综合展示大学生当前的实践水平及思想道德素质,对学生的综合素质测评会产生较大的影响,对此,教师要从评价传导机制上给予学生正确引导。第二主成分中绝对值相对较大的载荷系数代表的是学生的学习成绩及自学情况,说明学生的智育素质会对其形成比较全面的影响。
统计以上指标数据之后,将其标准化为以下形式:Y1、Y2、Y3、Y4、Y5、Y6。分析上述表3中的各项数据,分别除以学习成绩、政治教育水平主成分对应的特征值,再开平方根能够获取思政水平、学习能力中所有指标对应的系数。同时,由此获取思政水平、学习能力表达式:F1=0.387Y1+0.448Y2+0.435Y3+0.379Y4+0.396Y5+0.435Y6;F2=0.637Y1-0.100Y2-0.320Y3-0.544Y4+0.619Y5-0.232Y6。
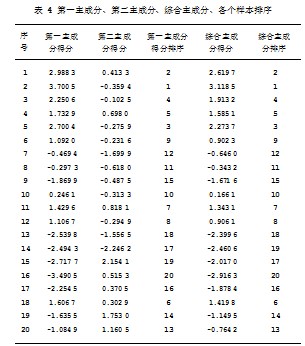
按照主成分表达式能够计算出所有主成分的得分,再综合分析学生的学习成绩得分,对所有的样本进行排序,但是因第一主成分未超过85%,难以获取足够的信息量,排序结果会有较大的片面性,故而需对综合主成分的总计得分情况进行系统的计算,以各个主成分的特征值为基础提取所有主成分的特征值和,并按照其比例分配权重,最后计算出综合主成分得分,以综合主成分得分状况对主成分样本进行排序。排序结果具体如表4所示。
结合表4,综合考量14、15号这两位学生的综合素质测评数据,可发现14号学生在一些重要指标上均落后于15号学生,如在学习升级、政治教育水平、自学情况方面,14号学生分别为56分、70分、60分,而15号学生则为76分、75分、80分,因此可知,15号学生排名将会高于14号学生。由此可见,若是第一主成分整体贡献率在85%以下时,其综合素质测评成绩排名可能存在误差,需通过综合主成分模型再次排序,如此可提升排名的真实性与公平性。
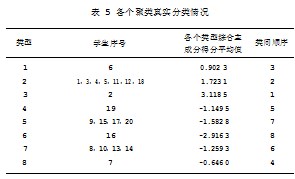
再次进行主成分分析,统计两个主成分得分,替代原始数据进行系统聚类分析。采用离差平方和法(Ward法)对以上20个样本中的第一主成分与第二主成分进行系统的聚类分析,最终获取聚类谱系图,从聚类谱系图可直观、清晰地看出各个样本的归类情况,再通过聚类图将所有的样本分为相似类群,按照类群的特征特性,将20个学生样本归纳为8个类型,并参考其综合主成分平均值实施类间排序,统计结果如表5所示,其中排名越靠前,代表学生的综合素质水平越高,表明该学生在学习成绩、政治教育水平、德育素养、宿舍执勤情况、自学情况、实践中的综合表现整体上占据优势。最后再对比分析主成分综合评价与聚类分析结果,两者比较契合,代表该种测评方式可行性较高,且具备较高说服力,因此该方法可以为大学生综合素质评价提供一种行之有效且较为科学的方法。
四、结语
以上就主成分聚类分析法在大学生综合素质测评中的应用进行了论述与分析,实现了对学生综合素质的合理测评,得出了较为客观、科学的评价,具备较强的可靠性。与常用的主成分分析法相比,该方法能更加科学、合理地对学生的综合素质做出评价。根据综合测评结果可知,部分大学生在学习成绩方面虽然取得了不错的结果,但是在其他方面缺乏协同发展,因此建议高校能够在关注学生成绩的同时,重视政治教育、德育、实践教育等,以此推动学生的全面发展,增强其综合素质,如此才能更好地应对当前社会中的诸多挑战[8-10]。
参考文献:
[1]李俊杰.大学生综合素质测评体系探索及思考[J].湖南医科大学学报(社会科学版),2008,10(6):205-208.
[2]张润.大学生综合测评体系变革探析[J].华南师范大学学报(社会科学版),2009(3):141-143.
[3]侯小洁,张俊华.基于分组主成分分析法的大学生综合素质测评研究[J].赤峰学院学报(自然科学版),2018,34(8):144-148.
[4]钱浩韵.基于主成分分析法的学生成绩评价[J].南京工业职业技术学院学报,2017,17(4):21-24.
[5]刘璐,杨景明,赵会仁,等.主成分聚类分析在学生成绩综合评价中的应用[J].辽宁工业大学学报(自然科学版),2012,32(3):200-204.
[6]黄会明.主成分分析法在大学生综合素质评价中的应用研究[J].重庆电子工程职业学院学报,2013,22(2):79-81.
[7]陈胜可.SPSS统计分析从入门到精通[M].北京:清华大学出版社,2010.
[8]李依沙.新时期大学生综合素质测评体系探究[J].质量与市场,2020(16):29-31.
[9]田原,莫蕴茜.独立学院大学生综合素质测评体系设计探索研究[J].才智,2019(31):115.
[10]张静.大学生综合素质测评理论研究述评与展望[J].佳木斯职业学院学报,2019(2):103-104.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/50081.html

 是第j列的平均值,
是第j列的平均值, 是第j列的标准差。标准化处理不改变各个指标间原本的相关系数。
是第j列的标准差。标准化处理不改变各个指标间原本的相关系数。 。
。