初等数论在中小学数学教科书中的融合应用论文

SCI论文（www.lunwensci.com）:

摘要：初等数论主要研究整数的性质与规律，与中小学数学内容有着密切联系。本文以学习理论为依据深入分析在中小学数学教学过程中渗透初等数论知识的意义与价值，以及初等数论在中小学数学教科书中的具体应用。基于研究分析，本文强调数学教育者需要不断提高自我专业能力和个人文化素养，培养终身学习的理念。

关键词：初等数论；中小学数学教科书；融合应用

本文引用格式：余晨伊等.初等数论在中小学数学教科书中的融合应用[J].教育现代化，2019，6（66）：260-262.

一 问题提出

初等数论在国内主要开设于高等院校，在中小学并未直接设立课程，但在该阶段的数学知识学习过程中，许多关键概念及原理都渗透着初等数论的理论，如：数的整除、带余数除法、因数与倍数、质数与合数、勾股定理等。尽管初中阶段的数学以代数、几何为主，没有较多初等数论的内容，然而，在高中甚至后续的数学学习过程中，关于整数的部分，必不可少地将会涉及到初等数论的理论，故在初中数学教学中有必要补充和延伸与教学内容相关联的数论知识。

较多学者对初等数论课程的教学现状与教学改革进行了考察与研究，尤其强调在高等师范院校的小学教育专业开设这门课程的必要性；也有大量期刊论文、硕士论文对初等数论在数学竞赛试题中的应用进行分析，但从整体上看，针对初等数论具体应用于中小学数学教科书的研究相对较少。另一方面，人教版数学教材是全国义务教育阶段数学学习的主流教材之一，具有较广的普及范围和较强的影响力。本文将主要分析初等数论在现行一至九年级新人教版教科书中的融合应用。

二 研究方法

本文主要采用了文献研究法和案例研究法等。基于数据资料库、图书馆等途径，进行大量文献检索，并搜集、梳理、分析相关资料；同时，通过研究案例，将理论与实际结合，梳理初等数论在中小学数学教科书中的具体应用，并对案例进行系统理解与深入分析，了解初等数论在中小学数学教学过程中的意义与价值。

三 初等数论融合于中小学数学教科书中的案例分析

（一）有余数的除法

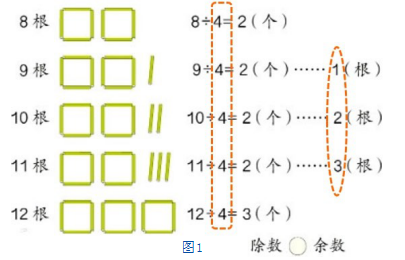
学生在小学阶段已接触初等数论中最基本的内容——整除理论，但结合儿童心理发展规律，代入具体数值，联系生活实际，能够帮助学生理解并掌握知识。学生将在二年级学习“有余数的除法”，教材呈现出用小棒摆出正方形的活动情境，教师引导学生观察、归纳，让学生发现“余数要比除数小”的特点（如图1）。




在本单元中，最典型的实际问题是与“日历”相联系的题型（如图2），例如：六月份有30天，有几个星期？还多几天？观察生活中的日历，便能发现其中蕴含着同余理论，假若知道某月2号是星期二，则9号、16号均是星期二，日历中位于同一列的整数被7除后的余数相同。



（二）质数与合数

五年级学生将接触因数与倍数的概念，随即认识质数与合数，教材有一道习题：做一个100以内的质数表。所采用的方法是验证100以内的每一个数字：1既不是质数，也不是合数，故先将1划去，随即将2、3、5、7的倍数依次划去（2、3、5、7除外），剩下未划去的数即为100以内所有的质数。任意给定一个正整数N都可按照上述方法，将不超过 N的质数的倍数逐一划去，便可求出所有不超过N的质数。这种方法由希腊时期Eratosthenes发明而被称为幼拉脱斯展纳筛法。

（三）最大公因数的求法

五年级下册的教材中，求出两个正整数的最大公因数常用“分解质因数”的方法，后演变为“短除法”。随着学习能力的提升，学生会在中学阶段认识“辗转相除法”和“更相减损术”，它们分别记录于数学发展史上两本重要的著作《几何原本》与《九章算术》中，在课堂上介绍这两本著作，可以渗透与教学内容相关联的数学史与数学文化，让学生在学习数学理论之余，丰富个人的数学素养。

（四）数的整除特征

学生认识因数与倍数的概念后，五年级下册的教材描述了2,5,3的倍数特征：(1)个位上是0,2,4,6,8的数都是2的倍数；(2)个位上是0或5的数都是5的倍数；(3)若一个数各位上的数之和是3的倍数，这个数为3的倍数；换而言之，小学中“特殊数的倍数特征”在初等数论中即为讨论整数的整除性，根据特殊整数的整除特征可避免两数进行除法运算，便可判断出一个数能否被另一个数整除。设N为n+1位正整数，则N=a0+a1×10+a2×102+…+an×10n=anan-1…a1a0常用数字的整除特征有：

①2|N2|a0②5|N5|a0

③3|N3|a0a1…+an

④9|N9|a0a1…+an

⑤11|N11|（a0+a2+…）-（a1+a3+…）

在初等数论中，根据可除性的基本定理可证明上述常用数字的整除特征成立，尽管证明过程在小学数学教学过程中讲解并不适用，但教师仍需掌握其中的原理，把握难易程度进行针对性教学，在课堂上引导学生理解知识，进而提升自己的学科知识与教学能力。

（五）勾股数

勾股定理是中学数学学习阶段最重要的定理之一，它作为一座桥梁将几何与代数连接在一起，揭示了直角三角形边长之间的数量关系，“若直角三角形的两条直角边长分别为a,b,斜边长为c,则a2+b2=c2”，假若单独讨论这种特殊形式的二次不定方程a2+b2=c2的正整数解（称为勾股数），便属于初等数论的研究内容：定理 不定方程x2+y2=z2,2|x,(x,y)=1的全部正整数解为x=2ab,y=a2-b2,z=a2+b2,其中a,bZ,a＞b＞0,(a,b)=1,a,b一奇一偶.

（六）鸡兔同笼与百鸡问题

“鸡兔同笼”问题最早记录于我国南北朝时期的数学著作《孙子算法》，“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何”，被设计在四年级下册“数学广角”的模块中。教材主要引导学生通过假设、列表等方法逐步解决问题，培养学生逻辑推理能力及数学应用意识。

随着学生心理发展，以及所掌握的数学知识增多，七年级的学生便可用方程法解决“鸡兔同笼”的问题，列出相对应的二元一次方程组，进行消元、求解。为了提高学生主动探索问题的能力，教师可以在课堂中补充介绍“百鸡问题”供学生课下思考。与《孙子算法》同样纳入于“算经十书”中的《张邱建算经》也记录着一道数学趣题——“百鸡问题”“鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一。百钱买百鸡，问鸡翁、母、雏各几何”？这个问题看视为求解三元一次方程组，但通过消去其中一个变量并化简，便发现这是初等数论中所讨论的二元一次不定方程的求解问题，尽管研究不定方程并非初中数学阶段的学习内容，但学生通过课后自我探索，用其所学，也能找到问题的解决方法，例如穷举法、联系一次函数的图像与性质等等。这能够拓展学生的数学视野，培养学生的问题解决能力，带领学生感受数学史与数学文化。

四 结论与启示

教学过程是教育者“教”与受教育者“学”的相互过程，教学相长，教师对知识有着全面的了解，才可更好地将知识传输给学生，为学生提供更多未来发展的选择。如今，“核心素养”的教学理念让教育者不仅仅关注知识输出层面，而且重视学生的身心发展。初等数论蕴含着丰富的数学史与数学文化，在课堂上结合中小学生的认知水平和数学教师教学能力，对数学知识进行延伸可以开阔学生的数学视野，提高个人的文化素养。另一方面，教育者要不断学习，提高自我的专业水平，培养终身学习的理念，完善自己的知识结构。将理论与实践相结合，顺应时代发展，反思并改进教学方法，不断提升我国数学教育的水平。

参考文献

[1]闵嗣鹤,严士健.初等数论(第三版)[M].北京:高等教育出版社,2003
[2]义务教育教科书•数学1-12册[M].北京:人民教育出版社,2017.
[3]沈利玲.提高小学教育专业初等数论课的教学效果[J].赤峰学院学报(自然科学版),2010,26(12):6-7.
[4]谢红梅.《初等数论》课程渗透数学文化教学研究与实践[J].兵团教育学院学报,2013,23(01):39-43.
[5]李玉慧.高校初等数论课程教学中详讲、略讲和让学生自学相结合的几点思考——以小学教育专业为例[J].教育现代化,2018,5(36):312-315.


关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！
文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jiaoyulunwen/27674.html