摘要:目的基于双向长短期记忆神经网络(bidirectional long short-term memory,BiLSTM)建立临床用血需求预测模型,预测未来长短期的血液需求量。方法以2017—2022年费县人民医院输血科的临床用血数据为基础建立模型,利用多变量链式方程补全法(multivariate imputation by chained equations,MICE)进行缺失数据补全,将补全后的数据归一化后获得6个血液指标的整体变化趋势。在模型的搭建中,首先,将2017年1月—2021年1月的临床用血数据作为训练集,建立BiLSTM模型;然后,将2021年2月—2022年1月的临床用血数据作为测试集,并获得6个血液指标的预测结果。采用均方根误差(root-mean-square error,RMSE)及平均绝对误差(mean absolute error,MAE)衡量预测精度。结果与传统的LSTM模型相比,BiLSTM模型训练集损失函数的下降更平稳,且平稳后的训练集和测试集的损失函数分别下降了约0.01与0.02。同时,BiLSTM预测的6个指标的平均RMSE和MAE分别为74.18和71.54,相比较LSTM分别下降了33.027%和16.794%。结论BiLSTM可用于临床用血的长短期预测,为中心血站中血制品的制备和调度提供参考。
关键词:血液需求量,预处理,预测模型,双向长短期记忆神经网络
0引言
输血是现代医学治病救人的重要手段。近年来,我国无偿献血事业正不断发展壮大。然而,一方面,我国无偿献血事业的发展极不均衡,许多地区出现了“用血难”的现象[1]。另一方面,由于血液制品保存技术的限制,大量新鲜的血液制品调配不当。因此,如何建立准确的血液需求量预测模型便成为当务之急[2-3]。
目前,常用的血液需求量模型为神经网络模型。在神经网络模型中,按照发展的前后顺序依次为人工神经网络(ANN)、后向传播神经网络(BPNN)、递归神经网络(RNN)与长短期记忆神经网络(LSTM)。然而,即便是上述网络中效果最佳的LSTM神经网络,其预测效果也不佳。因此,迫切需要找到一种新型的血液预测类模型以进一步提高预测精度和稳定性。双向长短期记忆神经网络(BiLSTM)是一种较新颖的预测类算法,目前在血液指标预测中的应用处在空白阶段。一方面,血液指标的数据获取难度较大;另一方面,双向网络模型的搭建也是研究的难点。本研究所用数据来自费县人民医院,选择BiLSTM进行临床用血成分预测,旨在为建立合理的采供血计划提供参考以及在血液管理、临床调度以及供血平衡中发挥重要作用。
1材料与方法
1.1数据来源
为了对血液需求量实现准确预测,本文统计了费县人民医院输血科2017年1月—2022年1月的临床用血数据,包括冷沉淀凝血因子、去白细胞悬浮红细胞、去白细胞单采血小板、病毒灭活冰冻血浆、洗涤红细胞、病毒灭活新鲜冰冻血浆6项血液指标的使用量。按时间段将2017年1月—2021年1月的数据作为训练集,将2021年2月—2022年1月的数据作为测试集,所有数据均记为一个单位(U),且各血液指标的一个U均表示200mL。
1.2神经网络结构
1.2.1 LSTM神经网络
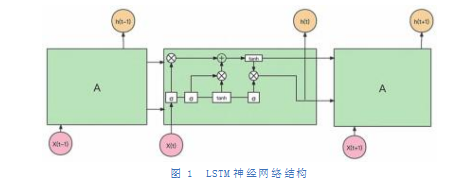
LSTM神经网络的基本原理是通过学习历史长期和短期的时间序列,建立长短期序列的相互关系,从而实现较好的预测效果[4]。LSTM神经网络的结构如图1所示:LSTM将隐含层的简单节点改进为存储单元。存储单元由输入门、输出门、遗忘门和记忆细胞组成。前向传播时,输入门和输出门分别决定了激活传入与传出存储单元;反向传播时,输出门与输入门分别决定了错误流入与流出存储单元。输入门、输出门、遗忘门是控制信息流的关键[5]。由于LSTM神经网络模型是在RNN的基础上发展而来,模型具有记忆久远细胞单元状态的能力,因此在长时间序列中LSTM通常具有比RNN有更佳的预测效果[6]。
设LSTM中xt及ht表示t时刻网络的输入值及输出值。令it、ft指输入门和遗忘门,则从xt到ht的映射关系为:
it=σWixxt+Wℑmt−1+Wicct−1+bi(1)
ft=σWfxxt+Wfmmt−1+Wfcct−1+bf(2)
式中,Wix、Wℑ、mt−1、ct−1、bi分别输入门中连接输入值的权值矩阵、连接上一时刻隐藏状态的权值矩阵、上一时刻隐藏状态的输出值、上一时刻记忆单元的状态、输入值的偏置矩阵;Wfx、Wfm、bf分别表示了遗忘门中连接输入值和隐藏状态的权值矩阵以及隐藏状态的偏置矩阵。
在式(1)和式(2)中得到it、ft后,ot、ct如式(3)、式(4)所示,分别表示输出门和记忆单元的状态。
ct=ft⊙ct−1+it⊙gWcxxt+Wcmmt−1+bc(3)
ot=σWoxxt+Wommt−1+Wocct−1+bo(4)
式中,Wcx、Wcm分别表示了记忆单元中连接输入的权值矩阵和连接上一单元隐藏层的权值矩阵;Wox、Wom、Woc分别表示了隐藏状态中连接输入值、隐藏层、记忆单元的权值矩阵;bc和bo分别表示隐藏层和输出层的偏式置矩阵。
根据t时刻的输出门和记忆单元状态的值可计算出隐藏层的输出:
mt=ot⊙yc(5)
⛝t=ηWcxmt+by(6)
其中,η表示softmax函数,g和y分别表示tanh函数。
1.2.2 BiLSTM神经网络
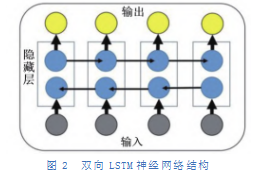
BiLSTM网络结构[7]如图2所示。
在每个时刻,双向LSTM神经网络均计算了正向和反向隐藏层的状态值,之后将两个方向在隐藏层的状态量加权求和,最后通过激活函数输出加权求和的结果值[8]。BiLSTM网络的计算公式如下所示:
ct=gWxtxt+Wctct-1(7)
ct’=gWxt’xt+Wct’ct+1’(8)
ot=ηWotct+Wot’ct’(9)
式中,Wxt、Wct、Wxt’、Wct’分别表示正向传播和反向传播中输入值权值矩阵和前一时刻的隐藏层权值矩阵,Wot和Wot’分别表示加权求和式中正向传播和反向传播的权值矩阵。通过双向LSTM神经网络可以建立历史值和未来值与当前值之间的关系,从而在更大程度上提高预测精度。
在BiLSTM网络中,双向的递归求解会使网络更快速地收敛到全局最优解,而且不易陷入局部最优解。随着梯度下降,整个网络会自动寻参达到最优解。本实验中,在前向主要将每个变量的前t时刻值作为模型的输入值,将每个变量的t+1时刻值作为模型的输出值,以此构建监督学习模型,以实现双向的长短期记忆递归预测;在后向将t=2至t=t+1时刻值作为模型的输入值,将t=1作为模型的输出值。通过双向的设置实现对每个时刻血液需求量的准确预测。
1.3研究方法
1.3.1数据预处理
预处理阶段主要进行缺失数据的补全以及数据归一化,以确保数据完整且具有相同的量纲。
(1)缺失数据补全:由于数据统计工作的限制,部分血液指标值缺失。各个指标值的缺失百分比见表1。
目前,现有的比较成熟的缺失数据处理软件包为Python里Sklearn中的SimpleImputer缺失数据补全软件包,内含中位数补全、平均数补全、链式方程法[9]以及K近邻法(K-nearest neighbor,KNN)。本文选择了链式方程法迭代补全,该方法的步骤:首先根据未缺失值建立链式方程,之后用缺失点插值该方程,将插值结果作为缺失数据点的各个血液指标的补全值,从第一个缺失点开始按顺序遍历直至遍历所有缺失数据点。经过补全后的缺失数据即可带入网络进行训练。
数据归一化是指将不同量纲的数据归一化到同一范围内,便于之后进行网络的训练与预测。本研究基于Sklearn工具的MinMaxScaler软件包进行数据的归一化。
1.3.2模型训练及测试
选用2017年1月—2021年1月的数据作为训练样本,用于预测2021年2月—2022年1月每个月6个血液指标的需求量。实验环境为Tensorflow2.5及Keras2.0深度学习框架,选择了Keras中的LSTM神经网络及BiLSTM框架;硬件环境中GPU为Google Colab提供的免费GPU,CPU选择Inter(R)i7-6700 CPU。在实验中,超参数的调整会影响网络训练及预测结果。对于BiLSTM和LSTM网络,训练样本的输入维度为48×1×6,其中输入样本的大小为48,时间步长为1,特征数量为6;输入的标签样本的大小为48×1,输出样本的时间步长为1,且样本数48。样本的Batch为4,学习率为0.01,迭代次数设置为50。
在训练前,需要将原始多元数据划分为监督学习的模型。对于LSTM网络,在当前时刻t的输入值为6个血液指标的前t-1时刻的数值,输出值为6个指标的第t时刻的数值;对于BiLSTM,在当前t时刻的输入值既包含6个指标的前t-1时刻,又包含了t+1时刻及之后的数值,输出值亦为t时刻的数值。模型在训练中定义损失函数为平均绝对误差(mean absolute error,MAE),如果MAE在训练过程中不再继续下降即停止训练。记录整个训练过程中的损失函数。
在模型训练后,针对建立的模型以及确定的参数,代入测试集并检验预测结果。本文使用均方根误差(root-mean-square error,RMSE)来衡量预测值与真值之间的误差水平。
1.4统计学分析
Python3.8软件中的Tensorflow2.5及Keras 2.0深度学习框架用于L STM和BiL STM网络的构建,SimpleImpute r软件包用于缺失数据补全,MinMaxScaler软件包用于数据归一化,Matplotlib软件包用于结果展示。在计算MAE和RMSE后使用平均相对误差(mean relative error,MRE)进行显著性检验,以确保本模型的残差序列满足白噪声要求。若预测结果在0.05显著水平之下,即在5%的相对误差要求以内,则认为预测结果符合要求。
2结果
本节展示了数据预处理、模型训练以及模型预测的最终结果。
2.1数据预处理
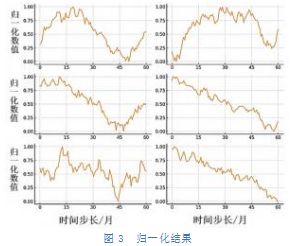
经缺失数据补全和归一化后的结果如图3所示。从左上到右下依次表示冷沉淀凝血因子、洗涤红细胞、病毒灭活新鲜冰冻血浆、去白细胞悬浮红细胞、去白细胞单采血小板、病毒灭活冰冻血浆。整体而言,冷沉淀凝血因子、去白细胞悬浮红细胞、去白细胞单采血小板、病毒灭活冰冻血浆呈现上升趋势,而洗涤红细胞、病毒灭活新鲜冰冻血浆的变化趋势则较为不稳定。
2.2模型训练结果
医疗信息化
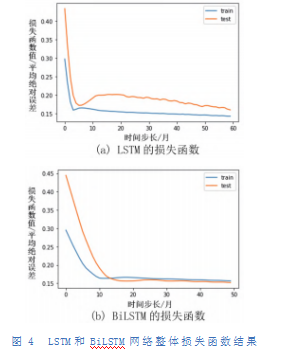
图4展示了LSTM和BiLSTM的损失函数,经过最初几次迭代后,LSTM和BiLSTM网络损失函数均呈现出迅速收敛的趋势。通过横向对比可知,LSTM模型在经历迅速下降后呈明显的上升趋势,BiLSTM的训练集损失函数持续下降并维持在一定的水平。所以,从整体上看,两种网络的损失函数均可收敛到较小的范围,但BiLSTM的模型表现优于LSTM模型。
2.3模型预测结果
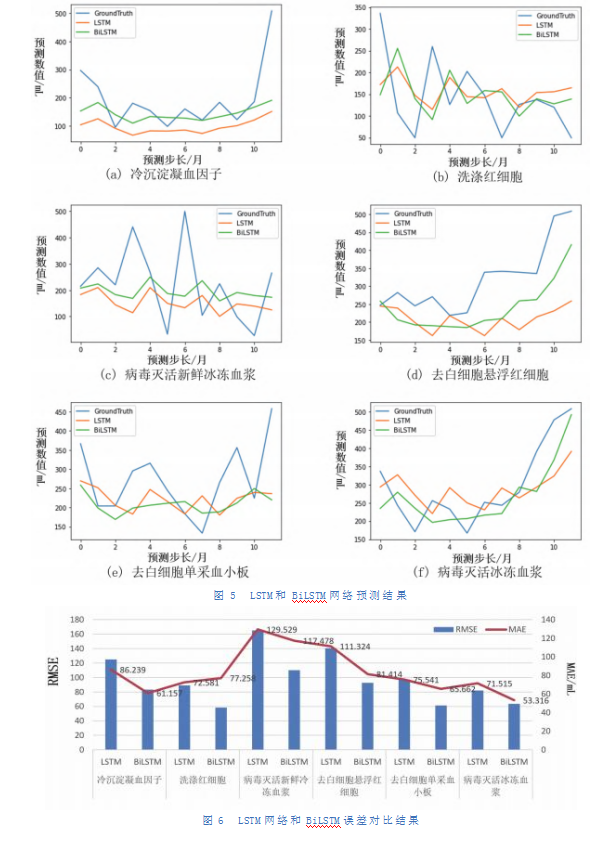
图5显示了LSTM和BiLSTM模型对6个血液指标的预测情况,将模型的预测值与其真值进行对比便可得到模型的误差水平。其中,纵坐标表示模型的预测值,横坐标表示时间步长。由于本文使用的软件为Python,Python中将坐标点0定义为预测步长1,即坐标点2为第3个预测步长。所以,由图5(a)可知,在第1个预测步长到第3个预测步长之间,LSTM模型的预测值更加接近真值,然而在经过第3个预测步长后,与LSTM模型相比,BiLSTM模型的预测值更加接近真值,即BiLSTM模型的预测精度更高,出现这种现象可能是由于冷沉淀凝血因子的数据波动性更大。而在图5(b)~(f)中,在整个预测步长内,BiLSTM模型的预测精度始终高于LSTM模型。所以,综上可以看出,在对血液指标预测时,BiLSTM模型表现优于LSTM模型。
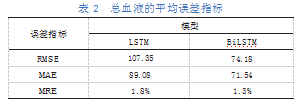
为了更加直观地对比BiLSTM模型和LSTM模型的误差水平,对图5中BiLSTM模型和LSTM模型的预测值与真值之间的RMSE和MAE进行统计,结果如图6所示。
由图6可以看出,与LSTM模型相比,BiLSTM模型的RMSE值和MAE值始终低于LSTM模型,这足以表明BiLSTM模型的精度更高,表现更优。比较两种方法的MAE可知,除了洗涤红细胞较接近外,剩下的所有血液指标中BiLSTM方法均优于LSTM;比较RMSE可知,BiLSTM在冷沉淀凝血因子、病毒灭活新鲜冷冻血浆和去白细胞悬浮红细胞的结果均显著优于LSTM,而剩下的指标里BiLSTM也优于LSTM。表2将图6中各个血液指标取平均值作为LSTM与BiLSTM的总误差指标,由表2可知,BiLSTM相较于LSTM,RMSE与MAE分别减少了33.17与17.54。
本文通过计算得知两种方法的MRE均小于5%,符合要求。
综上所述,无论是从整体上看还是从各指标的角度看,BiLSTM模型的表现均优于LSTM模型,并且BiLSTM模型不仅预测精度高,而且收敛速度快,在未来血液需求量预测方面发展前景光明。
3结语
对采血供血需求的准确预测,一方面,可以帮助中心血站更加有效地展开相关工作;另一方面,可以在保证满足临床用血需求量的前提下最大程度地节约资源。本文基于费县人民医院输血科获得的相关数据,利用LSTM模型和BiLSTM模型对输血需求进行多维度预测,研究结果表明BiLSTM模型整体上表现较好,模型的预测精度高。在血液需求量预测方面,BiLSTM模型应用前景光明。此外,本文对血液需求量准确预测方面的相关研究提供一定的参考价值。
参考文献
[1]黎世杰,陈锦艳,何军,等.临床血液需求预测数学模型的建立和应用[J].当代医学,2013,19(21):148-149.
[2]郑亚鹏,樊璐.基于LSTM的临床血液需求预测方法[J].计算机与现代化,2018(05):41-44,120.
[3]王岩,薛茜,杨蕾.应用季节周期回归模型预测临床血液需求量[J].新疆医科大学学报,2009,32(5):604-605.
[4]孙浩.血液供需预测模型及盈缺预警机制研究[D].成都:西南交通大学,2017.
[5]任艺柯.基于改进的LSTM网络的交通流预测[D].大连:大连理工大学,2020.
[6]王渊明.基于LSTM神经网络的电商需求预测的研究[D].济南:山东大学,2018.
[7]Mikhailov S,Kashevnik A.Car tourist trajectory prediction based on bidi-rectional LSTM neural network[J].Electronics,2021,10(12):1390.
[8]Razin M,Karim M A,Mridha M F,et al.A long short-term memory(LSTM)mod-el for business sentiment analysis based on recurrent neural network[M].Berlin:Springer,2021.
[9]Buuren S V,Groothuis-Oudshoorn K.MICE:multivariate imputation by chained equations in R[J].Journal of statistical software,2011,45(3):1-67.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/yixuelunwen/82768.html