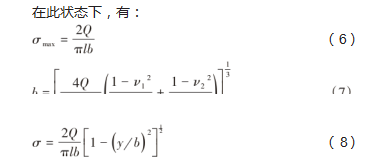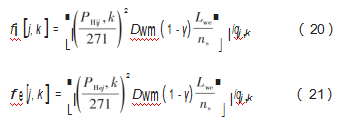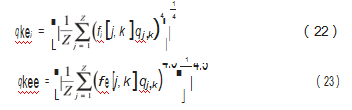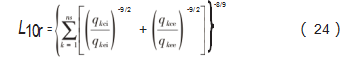摘要:风电机组轴承是高性能风机的核心部件,为了开发更高性能的风电机组轴承,需要对轴承的性能与寿命做出合理评价。基于轴承经典理论和软件仿真分析的结果,提出一种评价轴承性能指标的新方法。利用Romax软件搭建风机传动链柔性模型,以实际服役的风机机型为载体,在充分考虑风机所受复合载荷的前提下,分析滚动体修型量对于风机主轴轴承服役性能的影响。结果表明:所提方法能够考虑到轴系各部件的变形对于轴承滚动体载荷的影响,同时计算出较为合理的轴承风载合成寿命。对于滚动体不同修型量的比较,过小的修型量会导致应力集中,过大的修型量会造成接触区域变短,合适的修型量需要根据轴承受力情况具体分析。
关键词:风电机组,ROMAX模型,圆锥滚子轴承
0引言
随着如石油、煤炭等不可再生资源的过度开采,风能作为一种新兴的、环保的、成本低廉的可再生能源逐渐受到世界各国的关注[1-4]。而主轴轴承作为风机轴系的核心部件,其性能优劣直接决定了整个风机系统的性能上限。近些年,大兆瓦级海上风电主机的推广以及国家降低风机成本的趋势不可逆转,整个风电行业对于轴承厂家提出了日益严苛的技术要求。GL规范明确规定风电轴承的使用寿命不能低于20年[5],部分厂家甚至有更高的要求,而又因为风电轴承的吊装与维护成本高、难度大,造成风电主轴轴承失效的机理非常复杂,开展台架试验难度极大,因而风电行业广泛应用仿真技术分析滚动体-滚道接触应力并预测轴承寿命,仿真技术对于缩短风电轴承的研发周期、提高风机性能、降低风机成本都有着极为显著的作用[6-9]。
由于风载的特性是随机性、持续性、兼具冲击载荷与疲劳载荷,对风电主轴轴承的仿真分析一般可以分为疲劳工况和极限工况两种情况分开校核,而且在分析时一般会结合使用经典理论与软件仿真,即首先将复杂的实际风载转化为等效风载,再采用软件仿真获取滚道-滚动体接触应力及轴承寿命,而在仿真时,也需要结合相关的轴承理论和标准,如:ISO 281:2007、赫兹接触理论、L-P寿命预测模型等[10-12]。目前国内已经有很多学者采用数字-软件仿真相结合的方式对风电主轴轴承的失效机理和寿命预测进行了研究。文献[13]基于ADAMS建立了轴承多体动力学动态模型,对于轴承故障演化的机理进行了研究,获取了故障源激励与轴承动态响应之间的内在关系;文献[14]基于Romax建立了风机主轴传动链模型,探究了轴承游隙、轴承滚子密合度、轴承滚子修形和轴承跨距等设计参数对于轴承寿命和滚动体接触应力的影响;文献[15]基于ANSYS建立了某型号半直驱机组传动链模型,采用弹簧单元模拟轴承滚子,获取了单一载荷作用下轴承的受载特性及轴系的刚性。
以上研究主要是以某单一工况为主要研究对象,并不能完全反映出风机在实际工作过程中的实际受载情况。本文选取目前比较有代表性的某大型兆瓦级半直驱风电机组的传动链为研究对象,该机型包含上下风向两套单列圆锥轴承,并将该机型所受20年的复杂风载等效为16条载荷工况,再利用Romax软件建立多载荷工况下轴系柔性化模型,分析该模型下轴承的滚动体应力、疲劳寿命以及确定合理的修形量。
1滚动体-滚道接触应力计算
1.1赫兹弹性接触模型
工程上快速计算复杂风载下轴承滚动体-滚道接触应力时首先需要把问题简化,根据轴承经典理论,在接触区域的尺寸远小于接触体尺寸的理想条件下,圆锥滚子轴承的接触问题可以转化为赫兹接触中的线接触问题,滚动体滚道最大接触应力、接触变形量以及接触半宽可由轴承曲率函数及滚道滚动体之间的法向力来确定[16-17]。
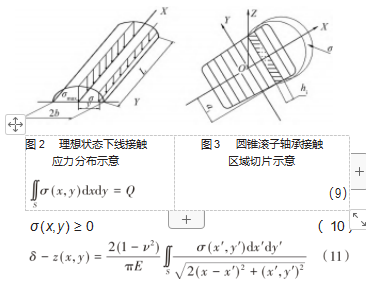
根据弹性力学的假说,理想状态下圆锥滚子轴承的接触区域的应力分布应该成为如图2所示的半椭圆柱形。
式中:L为滚动体有效长度;b为滚动体接触半宽;ν1、ν2为两种材料的泊松比;E1、E2为两种材料的弹性模量;y为沿滚动体母线的位置坐标;σ为该位置滚动体接触应力。
可以较容易地看出最大接触应力发生在接触区域中心位置,随着位置逐渐偏离中心,滚动体-滚道接触应力减小。而又因为在设计时滚动体-内滚道曲率和往往与滚动体-外滚道的曲率和不同,所以通常情况下轴承的最大接触应力会发生在滚动体与内滚道接触时,这也是校核轴承接触应力需要重点关注的点。
1.2滚动体切片原理
目前,简单的工程计算显然无法满足主机厂日益提高的分析要求。对于实际工况下的圆锥滚子轴承,考虑到修形量,滚动体母线相对于滚道的接触长度明显小于滚道长度且并非直线,再加上风载所包含的大弯矩导致的轴承偏载,甚至致使对风机主轴轴承进行应力分析时无法满足赫兹弹性接触的假设条件。因此,文献[18]引入一种目前行业上普遍接受的滚动体切片原理以计算单列圆锥轴承的非赫兹接触问题。
建立如图3所示的坐标轴,其中X轴为滚动体母线方向,Z轴为接触平面的法线方向,Y轴垂直于X轴与Z轴。根据滚动体受力平衡方程和变形协调方程,滚动体与滚道接触载荷以及接触变形可以通过以下公式表示。
式中:σ(x,y)为圆锥滚子与滚道之间的接触应力,MPa,由于接触应力为压应力,所以取值不小于0;S为接触区域,此处沿滚子母线进行了切片处理;E为弹性模量,MPa;ν为泊松比;δ为弹性趋近量,mm;Z(x,y)为两个接触体初始距离,mm,此处数值可以随着滚子母线方向存在变化,而不需要如赫兹弹性接触一般始终保持一致。
将圆锥滚子沿X轴方向进行切片,每个切片厚度假定为hi,切片总数为N个,假设每个切片的接触应力在滚子母线方向上均匀分布,而沿着滚子径向Y轴方向符合赫兹接触,则存在:
由上述公式,可以获得接触区域的应力分布情况以及每个切片的接触载荷,此方法也构成了Romax软件分析滚动体接触的基本算法,并可以在计算过程中考虑滚动体修形量对于接触应力的影响。
2轴承疲劳寿命的计算
2.1单一载荷作用下的计算
通常应用与风电主轴上的圆锥滚子轴承,其端部滚道容易产生边缘应力集中,使滚道表面产生剥落。为避免过早地发生此类次表面起源型失效,通常要对滚动体进行修形。根据滚动体切片的载荷和滚动体母线方向上的接触应力分布,可计算内外圈滚道上的应力修正函数:
式中:PHij,k与PHej,k分别为第j个滚动体的第k个切片分别与内圈和外圈滚道之间的接触应力,MPa;qj,k为第j个滚动体的第k个切片的载荷,N。
对于绝大多数的风电主轴轴承,轴承内圈和主轴配合一起旋转,轴承外圈安装于轴承座中处于固定状态。依照标准,计算基本额定寿命前需要计算轴承内圈某一切片对应于载荷施加方向旋转的当量动载荷qkei和轴承外圈某一切片对应于载荷施加方向静止的当量动载荷qkee,分别为:
式(22)对应轴承内圈,式(23)对应轴承外圈,由于在计算时引入了滚道的应力修正函数,故边缘应力的集中程度会极大地影响计算结果。所以,在当前条件下(内圈旋转,外圈静止),90%可靠度的风电主轴用圆锥滚子轴承的基本参考额定寿命为:
2.2多工况寿命合成方法
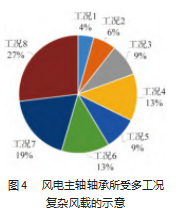
由于风电载荷的复杂性,单一工况的载荷条件下所计算出的轴承额定寿命是不足以表征轴承实际工作中受到复杂风载条件下的额定寿命的,需要对寿命进行合成。
当轴承受到如图4所示的复杂载荷时:工况1条件下轴承受载荷F1作用,时间百分比Tp1,计算额定寿命为Lp1;工况2条件下轴承受载荷F2,时间百分比Tp2计算额定寿命为Lp2;直到工况n条件下,轴承受载荷Fn作用,时间百分比,计算额定寿命为Lpn。引用文献[19-20]中和关于多载荷寿命合成的相关公式,对轴承的基本额定寿命和修正额定寿命分别进行合成:
3风电机组主轴轴承实例分析
3.1 Romax模型建立
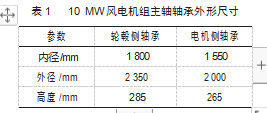
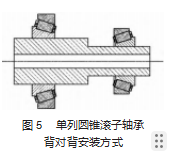
以某10 MW半直驱风电机组的传动链为例,机组主轴一端连接轮毂,一端连接电机,共安装两套单列圆锥滚子轴承,采用“背对背”安装方式如图5所示,轴承外形尺寸参数如表1所示。
在Romax软件中建立包含轮毂、主轴、轴承座、基座等的全轴系模型,设置轴承内外径过盈量、轴承运行温度、预紧量、润滑剂等计算参数,以计算其修正寿命。为更好地考虑到轴系的挠度,分析采用柔性模型的建模方式,各部件均需要转化为包含6自由度的FE模型再导入Romax软件中进行计算,模型如图6所示。
3.2载荷输入
由于风电载荷的特殊性和GL规范的相关要求,在分析风力发电机组主轴轴承时,需要考虑极限工况和疲劳工况两种情况,具体载荷数值由主机厂依据标准通过仿
真计算获得,其中极限载荷主要用来校核轴承应力安全系数,疲劳载荷主要用来校核轴承额定寿命。本文所采用的极限载荷共有16种工况,具体如表2所示。
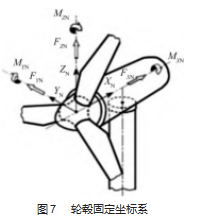
载荷方向为GL坐标系方向,如图7所示。
疲劳工况又可分为LDD载荷和LTS载荷,依据载荷种类的不同通常会包含几十到几百万条目的具体载荷数值(每个载荷条目均包含3个方向的拉力及两个方向的旋转力矩)。
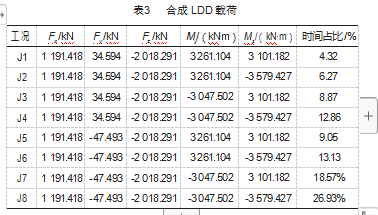
本文选用LDD载荷代入分析,为了方便计算,在计 算前首先已根据载荷的大小及方向进行合成,合成后共8组载荷工况,如表3所示。
3.3极限工况下滚子接触应力分析
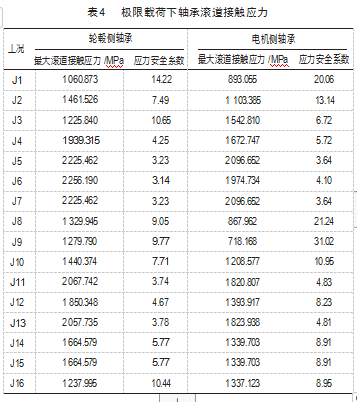
在极限载荷下,分析轴承的滚动体-滚道最大接触应力以及不同修形量对应力大小及应力分布的影响。初算首先对滚动体设置一个初始修形量,对极限16组载荷进行分析计算,计算结果如表4所示。由表可知,在J6工况下,轮毂侧轴承滚道接触应力最大,为2 256.19 MPa,故选用J6工况为代表,分析轮毂侧轴承滚子不同修形量下应力大小及分布情况;在J5及J7工况下,电机侧轴承滚道接触应力最大,为2 096.652 MPa,由于J5和J7载荷相同,故选用J5工况分析电机侧轴承滚子不同修形量下应力大小及分布情况。
3.3.1轮毂侧轴承滚子接触应力分析
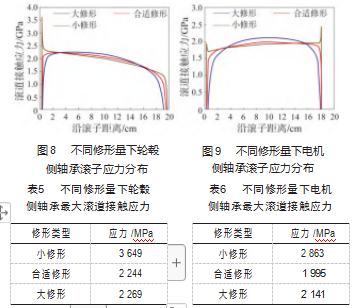
在J6工况下,对轮毂侧轴承滚子分别设置较小的修形量、较大的修形量以及经过调整后较为合适的修形量,分别计算并提取轮毂侧轴承的滚子应力分布状态。结果如图8、表5所示。由图8及表5可知,当滚子采用较小修形量时,在极限载荷作用下,滚子受载区域达到滚子有效长度的99.39%,但此时滚子出现边缘应力集中,最大接触应力高达3 649 MPa;当滚子采用较大修形量时,在极限载荷作用下,滚子受载区域相比较小修形量时有所下降,仅为94.56%,但此时滚子无应力集中,最大接触应力为2 269 MPa;当完成滚子修形量设计计算之后,取较为合适的修形量带入分析,从结果可以看出,此时滚子受载区域达到98.21%,相较于较小修形量,滚子接触区域并无明显降低,也未出现边缘应力集中,此时滚道最大接触应力为2 244 MPa,是三者之中的最小值。
3.3.2电机侧轴承滚子接触应力分析
在J5工况下,对电机侧轴承滚子分别设置较小的修形量、较大的修形量以及经过调整后较为合适的修形量,分别计算并提取电机侧轴承的滚子应力分布状态,结果如图9、表6所示。
从图9及表6可以看出,当滚子采用较小修形量时,在极限载荷作用下,滚子受载区域达到滚子有效长度的99.81%,但此时滚子两端均出现边缘应力集中现象,最大接触应力达到2 863 MPa;当滚子采用较大修形量时,在极限载荷作用下,滚子受载区域相比较小修形量时有所下降,仅为95.83%,但此时滚子无应力集中,最大接触应力为2 141 MPa;对滚子修形量进行设计计算后,取较为合适的修形量代入分析,从结果可以看出,此时滚子受载区域达到99.23%,相较于滚子较小修形量,滚子接触区域并无明显降低,也未出现边缘应力集中现象,滚道最大接触应力为1 995 MPa,也是三者之中的最小值。
3.4疲劳工况滚子接触应力分析
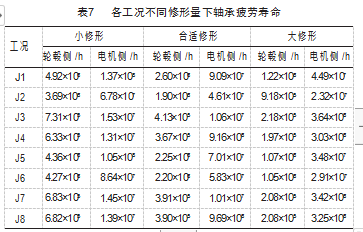
根据表3的LDD载荷,计算不同修形量下的轮毂侧、电机侧轴承的额定疲劳寿命L10m(修形量与极限工况计算时保持一致),分析滚子不同修形量对寿命的影响,计算结果如表7所示。
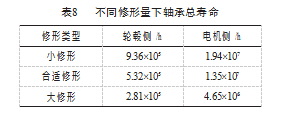
将其算出各工况下轴承的寿命进行合成,合成后的轴承总寿命如表8所示。从表可知,单一工况下计算出的轴承额定寿命与多工况合成的轴承额定寿命的结果有极大不同,单一工况下的轴承额定寿命并不能表征轴承实际工作情况下的额定寿命;滚子修形量的取值对轴承寿命也有较大影响,修形量过大会严重降低轴承的疲劳寿命,以滚子大修形量的寿命计算结果为基准,合适修形量下轮毂侧轴承寿命为1.89倍基准,电机侧轴承为2.9倍基准;小修形量下轮毂侧轴承寿命为3.33倍基准,电机侧轴承为4.17倍基准。
4结束语
通过在Romax软件中建立10 MW风电机组传动轴系的柔性模型,计算并分析了该传动链上两套圆锥滚子轴承在极限载荷条件下的接触应力分布和疲劳载荷条件下的额定疲劳寿命,研究了接触应力和额定寿命随着滚动体修形量的大小取值不同的变化规律,得出以下结论。
(1)和一般有限元软件相比,Romax软件求解更为方便,并且在计算中引入了轴承滚子切片的理论来计算滚动体-滚道接触应力,和轴承经典理论相比,Romax软件可以在计算时考虑套圈及轴系各部件的变形,更加符合实际工况,目前已得到风电行业的认可。
(2)滚动体修形量会极大地影响滚动体-滚道接触应力分布,当修形量较小时,滚道边缘产生显著的应力集中现象;随着修形量的增加,应力集中现象逐渐消失,但接触区域长度亦同样随之减少,最大接触应力会在到达一定数值后反增,因此修形量的选取并非越小越好。
(3)滚动体修形量同样会影响轴承的额定疲劳寿命,随着修形量的增加轴承的额定寿命同步增加。
(4)轴承设计时,需要针对不同机型具体的尺寸结构及受力情况进行分析,从而确定滚动体修型量。
(5)用单一工况下的轴承载荷不足以代表轴承在整个寿命周期内所受风载的综合情况,计算轴承在真实风载条件下的额定寿命须分开计算单一载荷下轴承的额定寿命并对寿命结果进行合成。
参考文献:
[1]郑林征.风电主轴轴承接触分析及优化设计[D].大连:大连理工大学,2016.
[2]舒印彪,张丽英,张运洲,等.我国电力碳达峰、碳中和路径研究[J].中国工程科学,2021,23(6):1-14.
[3]赵铭.风电主轴轴承试验机技术研究[D].大连:大连交通大学,2020.
[4]黎博,陈民铀,钟海旺,等.高比例可再生能源新型电力系统长期规划综述[J].中国电机工程学报,2023,43(2):555-581.
[5]GROUP A P M.DNV to certify wind turbines in South Korea[J].Asia Power Monitor,2022(614).
[6]王高峰,王燕霜,梁辉,等.风电主轴承失效分析与优化设计[J/OL].机械设计与制造:1-4[2023-08-08].DOI:10.19356/j.cnki.1001-3997.20230725.005.
[7]帅权,朱才朝,谭建军,等.机架柔性对双风轮风电机组传动链固有特性的影响[J/OL].重庆大学学报,1-15[2023-12-12].http://kns.cnki.net/kcms/detail/50.1044.N.20230530.1216.002.html.
[8]谭韶毅,白聪儿,王瑞良,等.风电机组变桨轴承滑移仿真及变桨系统振动分析[J].机电工程技术,2023,52(3):300-303.
[9]顾光成,刘勇,叶锋,等.风电机组载荷优化对变桨轴承力学行为影响研究[J].机电工程,2023,40(9):1419-1425.
[10]蒋玉孝,刘少军.ISO 281:1990与ISO 281:2007滚动轴承寿命计算标准的比较[J].机械强度,2015,37(3):6.
[11]牛宝禛,李伦,李济顺,等.基于多因素的风电主轴轴承疲劳寿命分析[J].轴承,2022(8):9-14.
[12]李云峰,范雨晴,王高峰,等.风电主轴双支承圆锥滚子轴承疲劳寿命计算[J].轴承,2023(6):26-35.
[13]田帅,张超,张辉.风电机组主轴轴承典型故障的建模与仿真分析[J].现代电子技术,2021,44(21):120-123.
[14]徐立晖,罗勇水,张明良,等.风电机组球面滚子轴承的参数化研究与仿真分析[J].机电工程,2021,38(7):929-934.
[15]李小伟.大兆瓦半直驱海上风电机组传动链系统建模及分析[J].风能,2023(6):66-73.
[16]HARRIS TA.Rolling Bearing Analysis[M].2nd ed.New York:John Wiley&Sons,1984.
[17]LUNDBERG G.Dynamic Capacity of Rolling Beariings[J].IVA Handlingar,1947,196.
[18]罗继伟.滚动轴承受力分析及其进展[J].轴承,2001(9):28-31.
[19]DNV G L.Machinery for wind turbinesStandard:DNVGL-ST-0361[S].DNV GL AS Oslo,Norway,2016.
[20]牛宝禛.风电调心滚子主轴承疲劳寿命及其可靠性分析[D].洛阳:河南科技大学,2022.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/78188.html