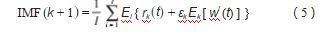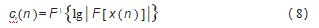基于 CEEMDAN 和倒频谱方法的圆锥滚子轴承振动信号分析*论文

SCI论文（www.lunwensci.com）

　　摘要： 圆锥滚子轴承运转过程中， 噪声信号往往会夹杂在振动信号中， 不利于信号分析。针对此问题， 提出一种自适应噪声完备 集合经验模态分解 (CEEMDAN) 与倒频谱相结合的方法对圆锥滚子轴承的振动信号进行分析。通过 CEEMDAN 算法对振动信号进 行分析处理， 消除残余辅助噪声， 减少噪声信号的影响; 采用倒频谱算法对处理后的振动信号进一步提取， 分析其周期性信号， 得到精确的振动信号频谱图。为验证所提方法的有效性， 对某圆锥滚子轴承 (30208H) 进行实验验证， 人为制造滚动体轻、中、 重 3 种不同程度的磨损; 采用所提方法对圆锥滚子轴承在正常、轻度磨损、中度磨损和重度磨损 4 种状态下的振动信号进行分析。 结果表明： 与单一的倒频谱分析法得到的频谱图相比， 利用所提方法处理后的频谱图， 圆锥滚子轴承的振动信号特征更加明显， 所提方法有利于准确确定圆锥滚子轴承的故障。

　　( 1. School of Mechatronics and Vehicle Engineering, East China Jiaotong University, Nanchang 330013. China; 2. Jiemu Bearing Group Co.,Ltd., Quzhou, Zhejiang 324200. China; 3. Hefei Institutes of Physical Science, Chinese Academy of Sciences, Hefei 230031. China)Abstract: During the operation of tapered rolling bearings, noise signals are often mixed with vibration signals, which is extremely unfavorable for signal analysis. For this problem, a method combining complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) and cepstrum is proposed to analyze the vibration signal of tapered rolling bearings . The vibration signal is analyzed and processed by using the CEEMDAN algorithm to eliminate the residual auxiliary noise and reduce the influence of the noise signal; the cepstrum is used to further extract the processed signal, and the periodic signal is analyzed to obtain an accurate vibration signal spectrum . In order to verify the effectiveness of the proposed method, a tapered rolling bearing (30208H) is experimentally verified. The rolling elements are artificially manufactured with three different degrees of wear, light, medium and heavy. The vibration signals of tapered rolling bearings in four states of normal, light wear, moderate wear and heavy wear are analyzed. The results show that compared with the spectrum map obtained by single inverted spectrum analysis, the proposed method is beneficial to accurately determine the fault of conical roller bearing .

　　Key words: tapered rolling bearings; vibration signal analysis; CEEMDAN algorithm; cepstrum analysis

　　0 引言

　　轴承是各类机械的关键部位之一， 其功能是将旋转 轴和旋转部件支承在轴上， 确保轴旋转在正常的范围 内[1-2]。而圆锥滚子轴承作为机械领域常用的滚动轴承之 一， 具有良好的刚性， 通过滚动体外周面的锥度， 可以 承受多个方向的载荷， 同时能够承受较广范围的载荷。 轴承承受的轴向载荷大小主要取决于该轴承接触角大小， 外滚道角度越大， 其承受轴向载荷的能力越强。因此， 圆锥滚子轴承运行情况直接关系到机械整体运转的状态 及工作效率[3]。

　　在圆锥滚子轴承的使用过程中， 各种因素都有可能会损坏轴承， 导致故障产生。因此， 在圆锥滚子轴承早 期发生故障时， 应迅速故障诊断和排除故障， 及时止损， 确保机械设备的正常运行。目前许多滚动轴承诊断与故 障检测的方法， 如振动信号分析、噪声分析、声辐射分 析等。由于振动信号分析具有故障特征信息丰富、采集 简单、易于实现状态监测等优点， 已被广泛应用于滚动 轴承故障诊断。由于滚动轴承在机械工作时的振动信号 具有周期性和往复性[4]， 可以通过振动信号的循环平稳 度函数来确定机器有无产生明显波动或噪声， 从而对轴 承的健康状况进行初步判定。

　　信号分析是圆锥滚子轴承故障检测的关键， 其主要目的是将提取出的复杂信号分解成若干简单信号的分量， 或者用一组有限的参量去表示一个复杂波形的信号， 根 据这一系列分量或这一组有限的参量去考察该信号在各 方面的特性。同时， 信号分析还能够从多角度获取信号 源的特征信息， 通过提取分析信号特征， 得到信号源运 行状况和特性等信息， 这也是故障诊断的基础。基于此， 振动信号检测方法主要包括经验模态分解 (Empirical Mode Decomposition， EMD ) [5-6] 、 集 成 经 验 模 态 分 解 (Ensemble Empirical Mode Decomposition， EEMD ) [7-8] 和 支 持 向 量 机 (Support Vector Machine， SVM ) [9- 11] 等 。 由 于 EMD 算 法 在 信 号 分 析 提 取 过 程 中 容 易 出 现 模 态 混 叠 现 象， 研 究 人 员 提 出 了 互 补 集 合 经 验 模 态 分 解 (Complementary Ensemble Empirical Mode Decomposition， CEEMD ) [12] 算法。然而， CEEMD 和 EEMD 算法虽然在 待分解的信号中加入了成对正负的高斯白噪声， 在一定 程度上减轻了 EMD 分解的模态混叠现象， 但是这两种算 法分解信号所得的本征模态分量中仍然残留少量的白噪 声， 会影响后续对信号的分析与处理， 同时导致计算量 翻倍， 效率降低。

　　当圆锥滚子轴承处于损坏状态， 其对应的振动信号 与正常状态下的信号存在差异。信号中不仅存在故障导 致的非平稳和非线性的信号， 还含有机械运动过程中产 生的噪声信号[5]， 利用现有的方法不足以真正实现实时 信号检测。

　　自 适 应 噪 声 完 备 集 合 经 验 模 态 分 解 (Complete EEMD with Adaptive Noise， CEEMDAN ) [13- 16]将正、负高 斯白噪声信号加入到经 EMD 分解后含辅助噪声的 IMF 分量， 并逐次迭代。 EEMD 分解和 CEEMD 分解是将经 验模态分解后得到的模态分量进行总体平均， CEEM ⁃ DAN 分解则不同。 CEEMDAN 分解是在得到第 1 阶 IMF 分量后就进行总体平均计算， 得到最终的第 1 阶 IMF 分 量， 然后对残余部分重复进行如上操作， 这样便有效地 解决了白噪声从高频到低频的转移传递问题， 同时大大 提高了计算效率。

　　倒频谱是指信号功率谱对数值进行傅里叶逆变换的 结果[17- 19]。倒频谱变换通过可以变换复数的功率谱， 通 过一系列卷积或乘积， 取对数变换为简单的和形式， 得 到识别信号的主要成分。正常实验过程中很难通过功率 谱对边频的总体水平作出定量的评估， 而倒频谱分析则 能够较好地提取出功率谱上的周期成分， 将原谱上成组 的边频带谱线简化为单根谱线， 对边频成分具有“概括” 能力， 便于观察。白泽瑞等[20] 通过倒频谱的风力发电机 齿轮箱多故障诊断方法， 对风力发电机齿轮箱中轴承和 齿轮上同时存在的多种故障进行有效地特征分离和准确 诊断。辛卫东等[21]采用倒频谱对风电机组传动链进行振动信号分析和故障诊断， 该方法能够清楚表征各种工作 情况下信号的故障状态， 同时能够在一定程度上反映故 障的发展趋势。

　　本文以某圆锥滚子轴承 (30208H) 为研究对象， 结 合 CEEMDAN 算法与倒频谱分析， 提出一种基于 CEEM⁃ DAN 和倒频谱的圆锥滚子轴承振动信号分析方法。对圆 锥 滚 子 轴 承 故 障 状 态 下 的 振 动 信 号 进 行 分 析， 利 用 CEEMDAN 对噪声信号进行提取并分解; 通过倒频谱法 对去噪信号功率谱的对数值作傅里叶逆变换， 随后提取 出其中的周期性冲击信号。结果表明： 该方法提高了振 动信号的信噪比， 抑制了在 EMD中的模态混叠现象; 与 EEMD 和 CEEMD 相比， 该方法提高了计算效率和故障诊 断的准确性， 验证了该方法应用于圆锥滚子轴承振动信 号分析与故障诊断中的可行性。

　　1 CEEMDAN 算法

　　CEEMDAN 算 法 可 以 在 一 定 程 度 上 减 少 EMD 和 EEMD 方法中存在的模态混叠、附加模态、残余噪声以 及计算量大等问题。不同于一般信号分析方法在分解信 号过程中添加高斯白噪声， CEEMDAN 算法在分解的各 个阶段加入的是特定的噪声， 不仅可以解决 EEMD 方法 的问题， 准确实现信号分解， 并且其循环迭代时间也只 有 EEMD 方法的 1/2.

　　为更好地理解 CEEMDAN 算法， 定义算子 Ek ( · )， 用 于求解 EMD 分解的第 k 个模态分量 IMFk， ωi 为服从 N( 0. 1) 分布的白噪声， εk 为第 k 个阶段所添加的白噪声 的幅值系数。CEEMDAN 方法的分解过程如下所示。

　　( 1) 在原始信号中添加白噪声 X(t) + ε0 ωi (t)， 随后 对其进行 EMD 分解， IMF1 为分解结果的平均值。


　　将白噪声 r 1 (t) + ε 1 E 1 [ ϖ i (t) ]， i=1. 2. …， N加入 第 1 阶段的剩余分量中， 并进行 EMD 分解， 则由第 1 个 IMF 的均值可以计算得到 IMF2.

　　( 3) 将白噪声 rK (t) + εK EK [ ϖ i (t) ]， i=1. 2. …， I 加入至第 k 个剩余分量， 并进行 EMD 分解， 则由第 1 个 IMF 的均值可以计算得到 IMF (k+1 )。

　　( 4) 重复第 (2) 和第 (3) 步， 直至剩余分量不能再进行 EMD 分解。最后， 得到的剩余信号为：

　　式中： K为分解所得到的模态分量个数。

　　重构的信号可以表示为：
　　2 倒频谱分析

　　圆锥滚子轴承的振动故障信号常常呈现周期性冲击 信号。由于调制和边带的影响， 功率谱通常不能定量地 估计边带的总体水平。同时， 在振动信号的检测中， 由 于传感器的安装位置和传输路径的不同， 导致信号的传 输函数和功率谱产生差异， 所测定的振动信号因传感器 安装位置的不同而不同。同时， 圆锥滚子轴承实际工作 时是安装在机械设备上的， 当其运转时， 故障噪声淹没 在强背景噪声中， 使信噪比大大降低。针对上述故障信 号中边带的影响， 倒谱分析可以用一条谱线表示这些边 带谱线， 便于采集和分析故障信号频谱上难以观测到的 周期性信号， 进一步提高故障信号提取能力。

　　倒频谱分析是一种非线性信号处理方法， 在图像和 语音理等领域有多种应用。它被定义为是信号离散傅里 叶 变 换 (DFT) 的 对 数 幅 值 的 离 散 傅 里 叶 逆 变 换 ( IDFT)。根据倒频谱定义的不同， 其可以分为实倒频谱 和复倒频谱。

　　实倒频谱用于各种工程与机械中， 能捕捉到实验工程所需信号的相关信息， 实倒频谱 Cr 的定义如下。

　　式中： x ( n ) 为采集的信号; n 为离散时间序号; F 和 F-1 分别为 DFT 和 IDFT。

　　3 CEEMDAN 与倒频谱

　　圆锥滚子轴承振动信号传输过程中会出现信号衰减 和噪声干扰， 导致提取难度增大。为使振动信号提取效 果更加准确直观， 将 CEEMDAN 算法与倒频谱分析相结 合， 通过 CEEMDAN 算法对轴承振动信号进行分解， 消 除残余辅助噪声， 减少噪声信号的影响， 随后运用倒频 谱对处理后的信号进行进一步提取， 分析其周期性信号， 最后得到精确的振动信号图解。 CEEMDAN 与倒频谱结 合的振动信号分析方法流程如图 1 所示。

　　4 实验平台

　　4.1 数据采集对象

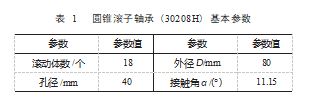
　　为验证所提方法的有效性和实用性， 利用 CEEM ⁃ DAN 与倒频谱算法对圆锥滚子轴承 (30208H) 的振动信 号进行检测分析， 提取出能够反映该圆锥滚子轴承的故 障特征。轴承基本参数如表 1 所示， 实验所用的圆锥滚 子轴承如图 2 所示。

　　4.2 实验数据采集设备

　　实验仪器设备为 BVT-8S 型轴承振动测量仪 (图 3)， 所用的振动传感器为 CA-YD- 187T52292 压电式振动传 感器， 数据采集器为 NI USB-4431.

　　5 实验结果

　　利用振动测量仪分别采集圆锥滚子轴承滚动体在轻 度磨损、中度磨损和重度磨损 3 种状态下的信号数据， 对振动信号进行提取分解和频谱变换， 并与正常状态 下的圆锥滚子轴承振动信号进行比较。实验台转速为 905 r/min， 采样频率为 25 600 Hz， 采样时间为 2 s， 每组 故障类型采集 50 组样本， 采样间隔为 10 s。

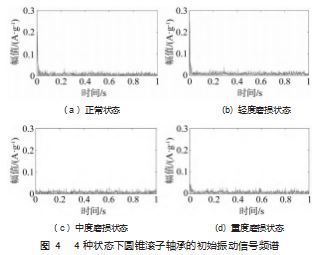
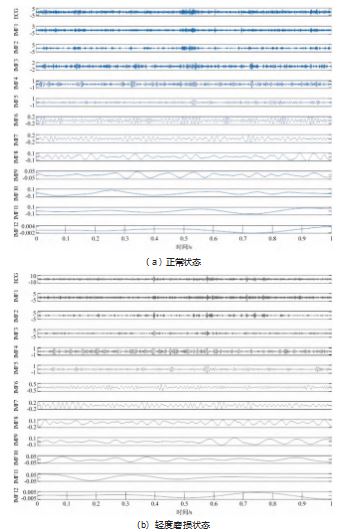
　　通过对采集到的振动信号进行频谱变换， 得到圆锥 滚子轴承滚动体正常状态、轻度磨损、中度磨损和重度磨损 4 种状态下的初始振动信号的频谱图如图 4 所示。由 图可知， 4 种状态下的振动信号频率大都集中在 0~0.05 A/g 区间， 轴承振动信号中含有较强的噪声干扰， 频率 成分复杂， 没有明显的故障特征， 因此需要进一步分析。

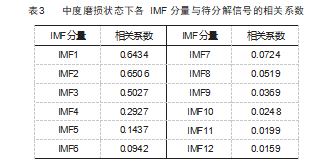
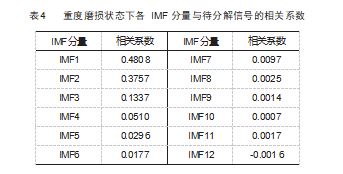
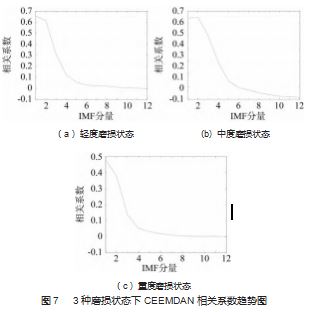
　　使用 CEEMDAN 对以上 4 种状态的圆锥滚子轴承振 动信号进行分解， 得到一系列 IMF 分量， 结果如图 5所示， 其箱型图如图 6 所示。将所得的各阶 IMF 分量 与原信号进行相关系数计算， 3 种磨损状态下的具体 相 关 系 数 值 如 表 2~4 所 示， 数 值 变 化 趋 势 如 图 7 所 示。其中， 原信号为输入信号， 比较值为 CEEMDAN 分解得到的各阶 IMF 分量， 相关系数表明了原信号和 各分量之间的相关程度， 值越大， 表明两者间的相关 性越大。

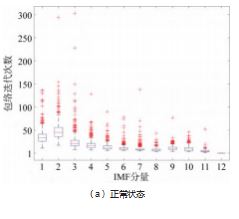
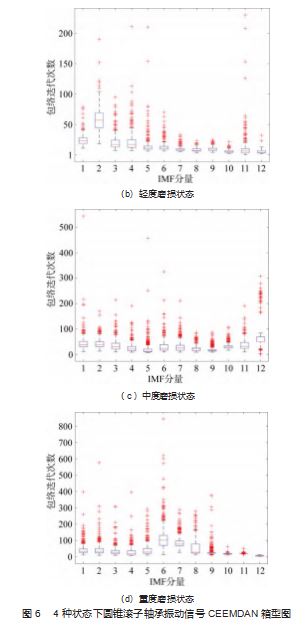
　　由 图 5 可 知， 大 多 数 冲 击 信 号 都 集 中 分 布 在 IMF1~IMF5. 而 IMF6~IMF12 所 含 冲 击 成 分 相 对 较 少， 故判定其为残余分量。通过图 6 的箱型图， 也可以直观 地识别出信号集中的异常值和数据离散程度。对比表 2~ 3 各 IMF 分量与待分解信号的相关系数数据与图 7 可知.


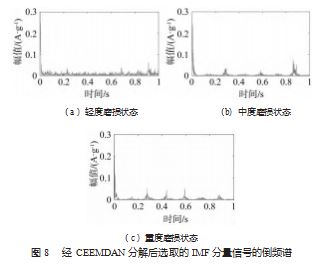
        3 种不同程度磨损状态下 IMF1 和 IMF2 分量与原信号相关 性较大， 综合考虑选取分量 IMF1 和 IMF2 进行倒频谱分 析， 结果如图 8 所示。对比图 4 和图 8. 图 8 中轴承故障 振动信号特征更加明显， 表明所提方法能够有效地对圆 锥滚子轴承振动信号进行分析， 可有效提取出该轴承的 故障特征信号， 区分轴承的不同工作状态， 为圆锥滚子 轴承的故障诊断提供理论依据。


　　6 结束语

　　本文针对圆锥滚子轴承振动信号传输过程中易衰 减、易受噪声干扰的特点， 提出了 CEEMDAN 与倒频 谱相结合的算法， 用于圆锥滚子轴承的振动信号分析。 使用 CEEMDAN 方法对圆锥滚子轴承滚动体正常状态、轻度磨损、中度磨损及重度磨损 4 种状态下的振动信 号进行分解， 然后筛选分解结果， 并对筛选后的 IMF 分量进行倒频谱分析。从筛选后的 IMF 分量的倒频谱 中可以准确找到圆锥滚子在不同磨损状态 (滚动体轻 度磨损、中度磨损及重度磨损) 时的故障特征， 从而 实现对圆锥滚子轴承故障的有效诊断与监测。与单一 的 CEEMDAN 算法或倒频谱算法相比， 所提算法能够 更加精确地分析圆锥滚子轴承的振动信号， 并提高了 计算效率。

　　参考文献：

　　[1] 李洋,李春,杨阳 . 基于 EEMD 及分形方法的轴承振动信号分析 [J]. 热能动力工程,2018.33(8):38-44.
　　[2] 王朝阳, 张涛, 吴鑫辉,等 . 分布式驱动电动汽车驱动电机轴承 故障诊断研究综述[J]. 机电工程技术,2023.52(6):36-40.
　　[3] 宋博峰 . 圆锥滚子轴承力学性能及疲劳寿命分析[D]. 西安: 西 安理工大学,2018.
　　[4] 王丹,金光灿,邱志,等 . 基于小波去噪和倒频谱分析的滚动轴 承内圈微弱故障诊断[J]. 煤矿机械,2020.41(12):160- 163.
　　[5] 高立龙 , 李九林 , 陈欣鹏 , 等 . 基于 EMD 及循环平稳度函数的 柴油发动机曲轴轴承振动信号分析[J]. 工程机械,2020.51(6): 1-6.
　　[6] KOPSINIS Y, MCLAUGHLIN S. Development of EMD-based de ⁃ noising methods inspired by wavelet thresholding[J]. IEEE Trans ⁃ actions on signal Processing, 2009.57(4):1351- 1362.
　　[7] 高淑芝,李天池 . 基于 EEMD 特征提取的滚动轴承故障诊断[J]. 沈阳化工大学学报,2022.36(2):151- 159.
　　[8] JIA Y, LI G, DONG X, et al. A novel denoising method for vibra⁃ tion signal of hob spindle based on EEMD and grey theory[J]. Measurement,2021.169: 108490.
　　[9] 张韦, 张永,骈晓琴,等 . 基于改进 EMD 样本熵和 SVM 的风机滚 动轴承故障诊断[J]. 机电工程技术,2021.50(12):38-41.
　　[10] 严孝强, 张振京, 宋业栋,等 . 基于优化 VMD 和 SVM 的柴油机 故障诊断算法[J]. 机电工程技术,2022.51(10):279-283.
　　[11] WANG M, CHEN Y, ZHANG X, et al. Roller bearing fault diag⁃ nosis based on integrated fault feature and SVM[J].Journal of Vi⁃ bration Engineering & Technologies,2021:1- 10.
　　[12] 崔芷宁, 于晓光,孙杰,等 . 基于 CEEMD 航空液压管路故障诊 断方法研究[J]. 机床与液压,2023.51(1):189- 195.
　　[13] GAO S, WANG Q, ZHANG Y. Rolling bearing fault diagnosis based on CEEMDAN and refined composite multiscale fuzzy en ⁃ tropy[J]. IEEE Transactions on Instrumentation and Measure ⁃ment,2021.70:1-8.
　　[14] 邱林江,花小朋,徐森 . 基于 CEEMDAN 与自适应阈值降噪的 滚动轴承故障诊断[J]. 机械与电子,2023.41(3):65-70.
　　[15] 郑锦妮,边杰 . 综合 CEEMDAN-SVD 与倒频谱的滚动轴承故 障诊断方法[J]. 太原理工大学学报,2021.52(3):495-501.
　　[16] LEI Y,LIU Z,OUAZRI J,et al. A fault diagnosis method of roll⁃ ing element bearings based on CEEMDAN[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechani⁃ cal Engineering Science,2017.231(10):1804- 1815.
　　[17] 高延,黄民,李宏亮 . 基于倒频谱的滚动轴承故障诊断[J]. 机械 工程师,2016(4):47-49.
　　[18] LIU Y,JIANG Z,HAIZHOU H,et al. Asymmetric penalty sparse model based cepstrum analysis for bearing fault detections[J]. Applied Acoustics,2020.165:107288.
　　[19] 王旭峰 . 基于倒频谱分析法的滚动轴承故障诊断研究[D]. 昆 明: 昆明理工大学,2010.
　　[20] 白泽瑞 . 风力发电机齿轮箱多故障诊断方法研究[D]. 保定:华 北电力大学,2020.
　　[21] 辛卫东 . 风电机组传动链振动分析与故障特征提取方法研 究[D]. 北京:华北电力大学,2013.
 
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/64913.html