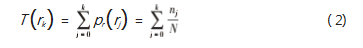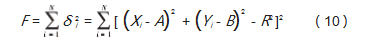SCI论文(www.lunwensci.com)
摘要:针对传统的机械接触式齿轮测量仪器操作复杂、易产生主观误差等问题, 提出一种基于机器视觉齿轮参数非接触式测量系 统。首先利用图像灰度变换、直方图均衡化方法对图像进行预处理, 提出小波变换模极大值法计算图像的矢量模值和相角, 寻找 梯度方向极大值点, 选取自适应阈值方法提取目标图像边缘。对齿轮的边缘轮廓形状特征, 采用最小二乘法拟合原理, 计算齿轮 的齿根圆直径、齿顶圆直径、齿数和模数等参数。以两种参数的齿轮零件测量为例进行实验分析, 结果表明, 测量值满足测量精 度要求, 证明了所提测量系统的可行性。
关键词:机械视觉,非接触式测量,齿轮参数测量,小波变换模极大值,最小二乘法
Gear Paramete Measurement System Based on Machine Vision
Chen Zhaowei, Fan Fanglei, Huang Weili
(College of Mechanical and Electronic, Donghua Polytechnic University, Nanchang 330013. China)
Abstract: Aiming at the problems of traditional mechanical contact gear measuring instruments, such as complicated operation and easy to produce subjective errors, a non-contact gear parameter measuring research system based on machine vision was proposed . Firstly, the image was preprocessed by means of gray scale transformation and histogram equalization . The wavelet transform modulus maximum method was proposed to calculate the vector modulus and phase angle of the image, find the maximum point in gradient direction, and select the adaptive threshold method to extract the edge of the target image. According to the shape characteristics of the edge profile of the gear, the least square fitting principle was adopted to calculate the parameters such as the diameter of the tooth root circle, the diameter of the tooth top circle, the number of teeth and the modulus of the gear. Taking the measurement of gear parts with two parameters as an example, the experimental analysis was carried out. The measurement results show that the experimental measurement values meet the measurement accuracy requirements, which indicates the feasibility of this measurement method.
Key words: mechanical vision; non-contact measurement; gear parameter measurement; wavelet transform modulus maxima; least square method
引言:齿轮是现代机械装备中应用广泛的重要传动类零件, 其几何精度直接影响着机械装备的工作性能和使用寿 命[1]。齿轮的轮齿形状多为渐开线曲面, 其几何形状较 为复杂, 涉及的几何参数也较多, 因此, 齿轮参数测量 一直是测量技术领域的研究热点与难点。目前, 齿轮的 参数测量多数仍然使用专用的精密测量仪器, 采用接触 式机械测量的方法进行测量和检测, 由于仪器操作复杂, 且多为单参数测量, 造成工作量大、耗时长、测量效率 低等问题, 同时, 还容易受人员主观因素影响而产生人 为误差。为了测量零件的实际尺寸, 设计非接触测量系 统, 降低上述影响尤为重要[2]。
随着计算机信息技术的快速发展, 零件的几何量测 量也出现了许多新技术和新方法[3]。其中, 机器视觉测 量技术以其高精度、高效率及非接触无损测量等优点广泛应用于工业生产领域[4], 如大批量生产线中的零件识 别、分拣、定位、缺陷检测和参数测量等。本文提出一 种基于机器视觉的非接触式齿轮参数测量系统, 以期实 现齿轮零件的多参数、实时在线测量工作。
1 测量系统组成
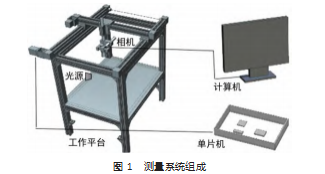
测量系统主要包括工作平台、 CMOS 相机、光源、 计算机和电机驱动系统, 如图 1 所示。系统在工作时 将齿轮放在载物台上进行拍照, 避免光照的强弱或者 其他因素影响图像的采集。然后使用计算机对齿轮进 行图像处理, 达到零件检测的目的。
2 图像处理
2.1 齿轮图像测量流程
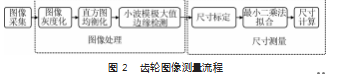
利用相机对齿轮进行图像采集, 将图像保存在计 算机内, 并对采集的图像进行处理来提取齿轮边缘轮 廓特征, 通过最小二乘法来计算齿轮尺寸, 最后与实际尺寸相比较判断其误差。具体图像预处理的流程如 图 2 所示。
2.2 灰度变换
将原图像转换为灰度图像可以降低处理时的计算复 杂度。灰度化用像素点的亮度值作为像素值, 亮度值可 以通过变换颜色模型, 采用加权平均法来计算:
Y = 0.299 × R + 0.587 × G + 0.114 × B ( 1)
由 R (红色)、 G (绿色)、 B (蓝色) 分量的线性加 权组合构成图像灰度化, 则把 3 通道的彩色图像变成单 通道的灰度图像, 如图 3~4 所示, 其中图像横纵坐标表 示图像像素值大小为 3 072×2 048.
2.3 直方图均衡化
将图像中像素个数多的灰度值进行展宽, 可以增加 像素之间灰度值差别的动态范围, 达到增强图像整体对 比度的效果, 使图像清晰, 从而达到增强的目的。对于一幅数字图像, 总像素数为 N, 第j 级灰度 rj 对应的像素 数为 nj, 直方图均衡化的变换函数 T(r)为:
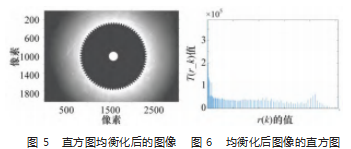
直方图均衡化后图像和均衡化后图像的直方图如下 图 5~6 所示。
2.4 基于小波变换模极大值图像边缘检测
针对齿轮图像处理引起的噪声干扰, 需要选择一种 既降噪又准确的边缘检测方法, 这是传统边缘检测方法 面临的一个问题[5]。由于目标图像的噪声, 光源的不均 匀产生图像边缘的阴影和相机的畸变, 因此采用小波模极大值边缘检测算法。首先, 用平滑函数对待检测图像 进行平滑处理, 经过小波变换, 得到对应小波系数, 然 后, 计算小波系数模的最大值, 最后, 用双阈值法检测 边缘。其具体过程描述如下。
( 4) 寻找梯度方向上取极大值的点。以 0° 、45°、 90° 、135° 、180° 、225° 、270° 和 315° 为中心, 将整个圆 周均分为 8 个 45° 角, 依次编号为 0、1、2、3、0、1、2、 3. 对应水平、45° 线、垂直、 135° 线 4 个方向, 判断沿梯 度方向值是否在某区域中的最大值, 则该点为模极大值 点, 即是为边缘点, 否则该点置 0.
( 5 ) 选取自适应阈值法去除噪声点, 确定边缘图像。 经过上述算法处理得出的齿轮的边缘还存在一部分伪边 缘, 所以还需要经过阈值处理去除[6]。采取单阈值法是 人为选定阈值去除伪边缘, 当选定像素点大于选定阈值 时, 则默认该点为边缘点。但采取这种方法有一定的弊 端, 如果选的阈值太大, 会丢失较弱的边缘, 如果选的 阈值太小, 检测的边缘会含较多的伪边缘。采用双阈值 法, 选取两个合理阈值, 会有效地保留边缘点并同时去
当局部模极大值大于高阈值时, 则该像素点是边缘 点, 保留; 当局部极大值小于低阈值时, 则该像素点不 是边缘点, 置 0; 当局部模极大值点介于高阈值和低阈 值之间的像素点, 检查该像素点领域内周围的 8 个点, 当这 8个点中有一个点的模极大值大于高阈值时, 该像素 点是边缘点, 保留, 否则置 0.得到最终边缘, 可以有效 解决噪声抑制和准确定位之间的矛盾[8]。结果如图 7 所示。
3 齿轮尺寸参数测量
3.1 尺寸标定
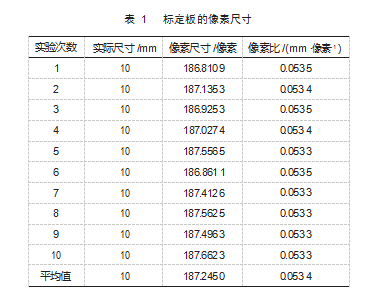
机器视觉的标定算法选用已知实际尺寸的标定板为 辅助工件, 令标定板和实验齿轮位于同一水平面上, 对 标定板和实验齿轮进行拍照, 采用 GP15012*9 的标定板 进行尺寸标定工件。用 SUSAN角点检测算法提取到的标 定板的角质点坐标。计算标定板任意两点在数字图像的 像素坐标系中的长度, 再把标定板在工件坐标系中的尺 寸和它在数字图像坐标系中的尺寸相比, 就得到了实验 的像素比, 完成尺寸标定工作。如图 8 所示。
计算两像素点坐标的像素距离 n, 将标定板的一格 真实尺寸 m 和像素距离 n 作商, 求出实验的像素比, 为 了把测量中引入的误差降到最低, 本次实验针对标定板 的像素尺寸采取 10 次重复实验, 计算出平均像素比。获 取标定板真实值和像素值之间的比例关系, 取 10 组实验 数据求平均值得到像素比为 0.053 4.如表 1 所示。
3.2 齿根圆、齿顶圆和齿数的参数确定
通过最小二乘法拟合齿顶圆和齿根圆半径, 依据最 小化误差的平方和来确定一组数据的最佳函数匹配, 其 具体拟合圆的原理如下:

其中, 圆心坐标为( A, B ), 半径为 R。
设样本集中的点为 (Xi , Yi ), 点个数为齿轮的齿数N, 为了得到最精确的拟合圆实际参数, 用样本点到圆心的 距离的平方与半径的平方作差[9], 即:
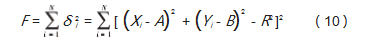
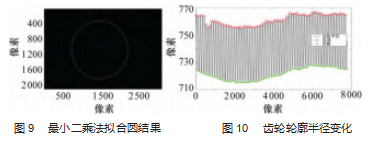
找出使得 F 最小的值, 即为最终解, 从而确定圆的 参数并拟合出圆。图像处理假如比较合理, 那么齿顶圆 和齿根圆的直径曲线就是标准的圆。所以距离圆心最远 的点的集合构成了齿顶圆, 最近的点的集合就构成了齿 根圆[10]。拟合圆如图 9 所示。
在正常情况下, 把齿轮轮廓从其中一个像素点展开, 齿轮边缘所有像素点到中心点的距离与其对应边缘标记 的位置是一个理想的周期函数, 并且对齿顶和齿根上的 所有峰值点做好标记, 更能直观表达齿轮轮廓半径的变 化趋势, 可以直接得出齿数。如图 10 所示。
3.3 模数的确定
齿轮模数的计算, 模数的确定可以用式(11) 计算:
4 结果分析
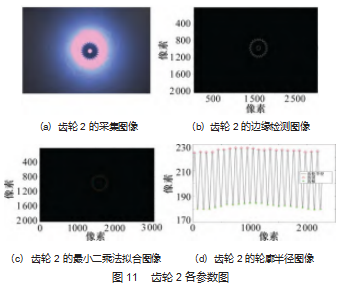
以两组不同尺寸的直齿圆柱齿轮为检测对象进行相 关参数测量, 来验证测量方法的准确性。依据齿轮 1 实 验测量步骤, 图 11 所示为齿轮 2 的采集图像、边缘检测 图像、最小二乘法拟合图像和轮廓半径图像。
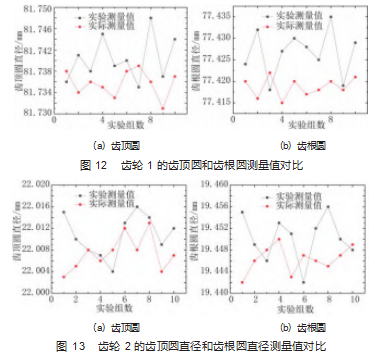
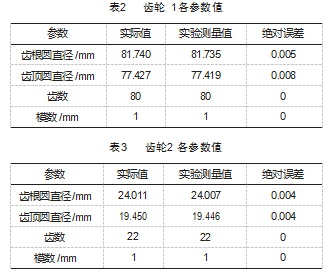
图 12 ~ 13分别为齿轮1和齿轮2的齿顶圆直径和齿根圆 直径的实验测量值和实际测量值变化分布。表2~3 所示为2 个齿轮 10 次实际测量平均值与实验测量平均值结果对比。
齿轮 1 的实验测量值与实际测量值二者之间的绝对 误差为 0.008 mm, 齿轮 2 的实验测量值与实际测量值二 者之间的绝对误差为 0.004 mm, 传统普通齿轮 8 级公差 测量精度为 0.03 mm, 测量精度在允许的范围内, 满足工业生产条件下直齿圆柱齿轮的测量精度。论证了该测 量方法的可行性。
5 结束语
本文以渐开线直齿圆柱齿轮为研究对象提出了基于 机器视觉齿轮尺寸测量方法, 运用图像预处理技术, 采 用小波变换的图像边缘检测, 成功提取了齿轮图像的边 缘信息, 用最小二乘法拟合齿轮直径, 得出齿轮齿根圆 和齿顶圆的像素直径。结合程序设计方法, 设计一套基 于机器视觉的齿轮参数非接触式测量系统。对齿轮的多 参数检测提供一定的借鉴。
参考文献:
[1] 王德祥, 张周强, 管声启 . 基于机器视觉的齿轮尺寸在线测量 系统[J]. 轻工机械,2021.39(2):67-73.
[2] 冯鹏鹏, 曾志强,李忠华,等 . 基于视觉技术的尼龙齿轮分度圆 测量[J]. 制造技术与机床,2020(1):132- 135.
[3] 杨云涛,关贞珍 . 基于机器视觉检测技术的齿轮几何参数自动 测量系统[J]. 计量与测试技术,2020.47(7):18-25.
[4] 李延浩 . 机器视觉在多领域内的应用[J]. 电子技术与软件工 程,2018(1) :93-94.
[5] 顾寄南, 高国伟, 丁卫 . 基于小波模极大值的工件图像边缘检 测[J]. 工具技术,2016.50(11):100- 103.
[6] 王煜,谢政 . 一种基于小波变换的改进 Normalshrink 自适应阈 值边缘检测算法[J]. 软件导刊,2020.19(9):206-209.
[7] 段军, 高翔 . 基于统计滤波的自适应双阈值改进 canny 算子边 缘检测算法[J]. 激光杂志,2015.36(1):10- 12.
[8] Qin Hu, Xing Xu, Dongbing Leng, et al. A method for measuring ice thickness of wind turbine blades based on edge detection[J]. Cold Regions Science and Technology, 2021.192:103398.
[9] 程亚彬, 张宏伟, 郭子路 . 基于最小二乘法拟合圆的矿车车厢 铆接孔检测技术研究[J]. 煤矿机械,2021.42(12):168- 171.
[10]王亚妮,胡有宁,李广文 . 基于最小二乘法的圆柱体油罐装置 拟合[J]. 西安文理学院学报(自然科学版),2017.20(6):11- 14.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63497.html