函数零点问题中参数范围的解法探究论文

SCI论文（www.lunwensci.com）　　　　

　　摘要:已知函数零点的个数，求解参数的范围是目前高考和模考考查的热点和难点．这类问题考查学生函数与方程之间的转化能力．利用参变分离法、分离函数法、数形结合等重要的数学方法可以灵活处理这类题型，提升学生的核心素养．

　　关键词:函数零点;导数;数形结合

       1 问题呈现

　　2总体分析

　　本题题设简洁，将函数、导数、零点等知识有机结合起来，多层次、多角度地考查了学生的数学思维和核心素养，同时考查了学生利用导数解决问题的能力，对逻辑推理、数学运算等提出了较高的要求．本题解法多样，可以直接利用参变分离法求解;也可以利用分离函数法解答，利用导数的几何意义，即切线的斜率求解入手，再从相切逆推至函数图象相交的情况，进而求出参数的取值范围;可以根据零点个数，分类讨论细化解题，求出a的范围;作为选择题，还可以借助题设和选项的特点，利用排除法得出正确答案．但每种方法操作均不容易，在解题过程中会碰到一些障碍．下面具体分享一下，希望能帮助学生找到解决这类问题的突破口．

　　3试题解答

　　评注这种解法要注意多次求导的目的，否则思路易乱．另外①处学生不容易想到，感觉从天而降．事实上，这是一种数学直观，对于含有超越式lnx的函数，我们应关注自变量为e，^e的函数值，这应该是经验主义和数学基本修养，根据实际需要进行验证．②处一定要作说明，以确认函数单调递减的源头和单调递增的尽头，进而保证交点个数不再有新变化，否则不能下结论．这一点学生容易想当然．下面举一反例:

　　共解，结合方程结构特征得x=^e是g'(x)=0的解．下同解法1．

　　评注此种处理方法需要较高的观察能力和配凑思维，值得我们思考和借鉴，提高解题能力．导数中有的零点是较难处理的，需要很多代数技巧作支撑，也要充分利用零点解题，尤其是隐零点，它可以帮助我们化超越函数为基本初等函数，还可能起到降次的作用，整体代换后还可能达到消元的目的．

　　视角2分裂原函数，构造新函数．

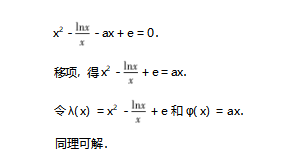
　　评注解法4和解法3有异曲同工之妙，本质是两个函数图象整体平移，不再赘述，感兴趣的同仁可以自行试验一下．事实上，构造函数没有特殊的要求，关键在于新函数易于研究，直观形象就好．这一点对学生来说是一个挑战，形异质同解法会带来解题创新思路，对学生的能力提升大有裨益．

　　当然我们也可以直接转化为函数f(x)=x3－ax2+ex－lnx的图象与x轴交点的个数，分类讨论求出参数a的范围，此法求解原则上可行，但运算量较大．讨论中要保证分类的科学性，做到既不重复，又不遗漏，是求解此问题的关键，限于篇幅，不再赘述．

　　视角3特值验证，小题速解．

　　评注作为选择题，为了节约考试时间，我们期待小题能小做，速战速决，所以结合题设及选项的结构特征，巧妙换元，特征值可排除错误选项，进而快速找到正确选项．这也需要学生有扎实的功底，在较短时间内发现非正确项的破绽．

　　4高考链接

　　通过对此题多种解题方法的探究和比较，能很好地提升学生分析问题和解决问题的能力，逐步培养学生的核心素养，提升学习效率，让学生所学的知识系统化．另外，分离变量、分离函数借助于数形结合是突破此类题的关键，尤其是曲线与直线相切地恰当使用．可以说，题目从知识立意、能力立意向价值引领、素养导向的转变，很好地体现了试题的甄别功能．因此，我们的教学，绝不能够仅仅停留在刷题的层面，一定要在能力和素养上下功夫．

　　参考文献:

　　[1]谢强，罗毅．基于函数零点个数求参数范围的几种解法———由一道高考题展开的思考[J]．高中数理化，2018(10):7－8．

　　[2]任志鸿．十年高考(数学2020年版)[M]．北京:知识出版社，2020．

　　[3]中华人民共和国教育部．普通高中数学课程标准(2017年版2020年修订)[M]．北京:人民教育出版社，2020．

　　[4]教育部考试中心．中国高考评价体系[M]．北京:人民教育出版社，2019．

　　[5]蔡海涛．探寻函数零点揭开参数面纱———从一道高考题谈起[J]．福建中学数学，2021(03):38－40．

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/63238.html