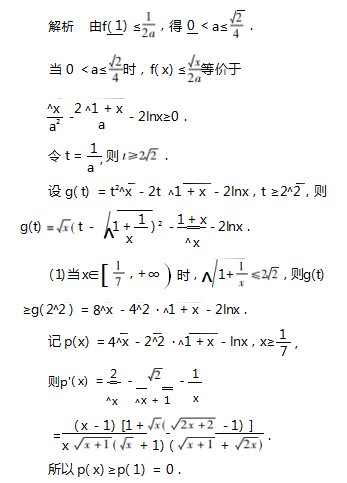SCI论文(www.lunwensci.com)
摘 要: 本文探究了高考导数压轴题中变更主元的几种处理策略,并分别从变更主元后构造超 越函数、构造幕函数、构造双勾函数和构造二次函数等几个视角对其进行呈现.
关键词: 导数,主元,构造,策略
函数与导数是培养学生逻辑推理、直观想象和 数学运算等核心素养的主要载体之一,其一直是高 考数学考查的重点内容.在处理函数与导数的压轴 题时,对零 点 的 处 理 往 往 是 一 个 关 键 环 节,有 些 超越函数( 指不满足任何以多项式作系数的多项 式形式的函数,如三角函数 、对数函数 、反三角函 数和指数函数等) 的零点确实存在,但无 法 精 确 求解,此谓之“隐零点”;有些导数的零点虽然可 求,但因含参而需要讨论.对于这类问题,常见的 处理方式主要有虚设零点 、化隐为显和变更主元 三大类.
本文主要探讨这类压轴题中变更主元的几种处 理视角.所谓变更主元,是指有些数学问题中常含变 量,在某些情况下若按常规思路确定主元可能会导 致问题复杂化,若能针对题目的结构特征人为地突 出某个变量的主体地位,将之当作主元构造新的函 数,则可达到化繁为简、化难为易的目的.这种问题 解决的思想方法也称为主元法.
下面结合近几年的部分高考导数压轴题来感受 这种策略,以供大家参考.
1 变更主元,构超越函数
评注 本题常规的一种做法是通过对 f( x) 进 行求导,结合第一 问的相关结论发现导函数有隐零 点,再虚设零点后进行消“超”代换( 指的是把超越 函数转化为普通函数),得到关于隐零点为自变量 的一个双勾函数,最终利用均值不等式或求导证得. 这种方法对学生的能力要求较高,这里采用了重新 构造关于变量 a 的对数超越函数,此法很好地避免 了隐零点的出现.
2 变更主元,构幕函数
例 2 ( 2016 年全国Ⅲ卷文) 设函数 f( x) = lnx -x + 1.设 c>1.证明: 当 x ∈ ( 0.1 ) 时,1 + ( c-1 ) x >cx.
证明 当 x ∈ ( 0.1) 时,设 h( c) = cx -cx + x-1.c >1.
则 h'( c) = xcx-1 -x = x( cx-1 -1) >0.
所以 h( c) 在 [1.+ ∞) 上单调递增.
所以 h( c) >h( 1) = 0.
所以当 c >1.x∈( 0.1) 时,1 + ( c -1) x>cx.
评注 本题常规的一种做法是通过构造函数 g( x) = cx -cx + x -1 再进行求导,得到导函数的零 点后,再结合前两问的相关结论对零点的范围进行 放缩,最终利用 g( x) 的单调性证得.这种方法其实 是命题者在“高考要体现选拔功能”的思想引领之 下给出的一种证法,这里采用重新构造关于变量 c 的幕函数,会发现根本不需用到前两问的结论就使 得问题得到完美解决!
3 变更主元,构双勾函数
评注 这里的证明思路主要是重新构造关于变 量 a 的双勾函数,再利用均值不等式实现消参的目 的.较之本题的常规做法( 即通过直接求导得到f( x) 的最值) 并没有优势,这是因为f '( x) 的零点并非是 隐零点,它可以直接求出来.这也提醒我们在解题时 不要盲目地进行主元的变更,有时变更可以事半功 倍,有时却可能导致事倍功半,所以应该具体问题具 体分析.
4 变更主元,构二次函数
次函数最 值 问 题.如 果 不 变 更 主 元 也 可 以,比 如 通过令 t = ^x 来构造关于 t 的超越函数,再通过放 缩消去参数 a 来求解.但较之变更主元的思路还 是过于繁琐( 虽然变换主元也并不算简洁) ,而且其换元( t = ^x)和放缩的技巧对学生的能力也是 一种考验.
通过上述几道真题我们知道,通过变更主元后 构造关于新元的超越函数、幕函数、双勾函数和二次 函数等函数进行求解,是处理导数隐零点等问题的 常见策略之一.在导数压轴题的教学过程中,像这样 以专题的形式介绍隐零点问题的处理策略,尽量一 次性彻底地解决与其有关的问题,对学生解题水平 的提升、逻辑思维的训练和核心素养的培养,想必都是极好的.
参考文献:
[1] 苏艺伟,张兵源.主元法巧解导数压轴题 [J].高中数学教与学,2020( 01) : 4-6.
[2] 侯希艳.导函数隐零点的处理方法 [J].高中数理化,2019( 03) : 19-20.
[3] 中华人民共和国教育部.普通高中数学课程标准( 2017 年版 2020 年修订) [M].北京: 人民教 育出版社,2020.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63075.html