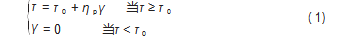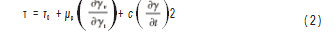CFD 自密实混凝土泵送性能模拟研究进展论文

SCI论文（www.lunwensci.com）

　　摘要： 自密实混凝土 (SCC) 因其更好的可泵性被广泛用于混凝土泵送施工。由于成本高、耗时久、且结果可重复性较低， 混凝 土的泵送性能实验研究已逐渐被数值模拟研究所取代。本文综述了自密实混凝土泵送规律的近期研究成果。归纳了 SCC 在泵送管 道流动过程中流速、压力损失等的变化规律。讨论了自密实混凝土在泵送过程中的流变规律。综述了自密实混凝土的流变模型在 国内外的研究进程， 分析了相关自密实混凝土模型的验证与改良及对一些自密实混凝土的流变性测试方法进行了统分。除对自密 实混凝土的流变模型进行分析外， 还描述了自密实混凝土在泵送前后的流变性能的差异。阐述了自密实混凝土微观状态下的 DEM 模型对坍落度试验的帮助， 对目前较为认可的自密实混凝土泵送规律评估模型作了评述。结果表明自密实混凝土在泵送过程在 CFD 的模拟下节省了大量的人力物力， CFD 自密实混凝土的泵送模拟发展还要再进一步完善， 目前的流变模型能够准确地预测混 凝土的泵送， 但要想得到一个最佳的参数还需要大量验证试验去减小误差， CFD 自密实混凝土的模拟还需要去不断完善。

　　Abstract: Self-compacting concrete (SCC) is widely used in concrete pumping construction because of its better pumpability . The

　　experimental study of pumping performance of concrete has been gradually replaced by numerical simulation research due to high cost, long

　　time-consuming, and low reproducibility of results. The recent research results of self-compacting concrete pumping law were reviewed . The

　　changes of flow velocity and pressure loss of SCC in the flow process of pumping pipeline were reviewed . The rheological law of self-

　　compacting concrete in the pumping process was discussed. The research process of rheological models of self-compacting concrete at home

　　and abroad was reviewed, and the verification and improvement of related self-compacting concrete models were analyzed . The rheological test

　　methods of some self-compacting concrete were divided . In addition to the analysis of the rheological model of self-compacting concrete, the

　　difference in rheological properties of self-compacting concrete before and after pumping was also described . The DEM model in the microstate

　　of self-compacting concrete in the slump test was described . The currently recognized evaluation model of self-compacting concrete pumping

　　law was reviewed. The results show that self-compacting concrete in the pumping process in the CFD simulation saves a lot of manpower and

　　material resources, CFD self-compacting concrete pumping simulation development to be further improved, the current rheological model can

　　accurately predict the pumping of concrete, in order to obtain an optimal parameter also need to do a lot of verification tests to reduce the error,

　　CFD self-compacting concrete simulation also needs to be continuously improved .

　　Key words: CFD; self-compacting concrete; rheological models

　　0 引言

　　混凝土泵送的起源可以追溯到 20 世纪 30 年代， 于 1927 年在德国推出， 于 20 世纪 80 年代在我国开始推广。 如今， 我国混凝土泵送技术已大范围运用在工程建筑中， 在超高层建筑和大跨桥梁建设领域的使用尤为广泛。泵 送混凝土不仅可以大幅度缩短建设时间， 还可以泵送到 许多人工难以浇筑的地方。经过 40 年的探索， 我国积累 了大量的混凝土泵送经验， 如超高程泵送混凝土的配制与施工技术[1-2] (如图 1 所示)、混凝土泵送过程压力变化 规律[3-4]、混凝土可泵性简易评价方法等[5-6]。现代混凝 土的泵送性能主要依赖坍落度， 压力泌水试验等经验性 参数和大型的盘管试验， 这些试验费时费力， 严重制约 现代施工技术的发展。因此需要提出合理的混凝土泵送 规律评估模型和测试方法。

　　对于混凝土的泵送规律研究并不多， 主要针对泵送 前的混凝土[7]。经过泵送后， 混凝土的许多性质都会发生改变， 其中混凝土的流变性变化最大， 即屈服应力与 塑性黏度的变化最为明显[8]。此外还有对泵送中的混凝 土单位长度的泵压损失研究[9]。现代科学技术对混凝土 的泵送研究主要基于 CFD 计算。本文主要总结了自密实 混凝土 (Self-compacting Concrete， SCC) 的泵送规律研 究进展， 并展望了未来的自密实混凝土泵送的研究。

　　1 国内外研究现状

　　自密实混凝土最早由日本学者提出。自密实混凝土 的流动性能较为优异， 在 1988 年试制成功后得到了广泛 应用， 其中应用较多的是高程泵送和远距离泵送[10]。混 凝土的质量、原材料、高效减水剂、粉煤灰等的加入会 使自密实混凝土的性能在泵送过程中发生变化。泵送技 术不仅用于施工现场的混凝土运输， 而且已经成为预制 混凝土工厂自动化混凝土交付和浇筑的趋势。现代泵送 技术的迅速发展使得泵送稠度较高的混凝土成为可能， 但最适合泵送的仍然是容易流动， 不太粘的混凝土。如 今， 新一代混凝土通常由粘合剂、骨料、添加剂、外加 剂、水和空气 6 种成分组成。自密实混凝土具有比传统 混凝土更高的黏度和黏性[11]。接下来主要介绍自密实混 凝土的流变模型， CFD 自密实混凝土的泵送仿真模型及 泵送规律。

　　2 SCC 流变性研究进展

　　2. 1 SCC 自密实混凝土流变模型

　　自密实混凝土一般被视为宾汉姆流体。宾汉姆流体 由 Fyes[12]等提出， 是美国学者 E.C.Bingham 最早发现并给 出表征该模型的两个重要参数： 屈服应力和塑性黏度。 宾汉姆模型由理想的圣维南体和理想牛顿流体组成。在 Tat[13] 的研究中， 宾汉姆模型可以准确描述新拌混凝土的 流变性能; Chong Hu[14] 提出， 当新拌混凝土的坍落度大 于 8 cm 时且没有发生严重离析时， 可将其视为宾汉姆材 料。宾汉姆模型是由弹性元件， 粘性元件， 塑性元件组 成。其表达式为：

　　试中：r为剪切应力;r0为屈服应力;η p 为塑性黏度; γ为剪切应变率。

　　当 τ < τ 0 时自密实混凝土为固态， 当 τ ≥ τ 0 时自密实 混凝土的内部结构被破坏， 进入液态， 按牛顿黏性规律 流动。因此自密实混凝土的泵送过程中需要时刻施加一 个外力使其保持流动状态。

　　Feys 等[15- 16] 发现， 采用宾汉姆模型研究自密实混凝 土的泵送时， 由于剪切速率的增加会使自密实混凝土产 生明显的黏度增稠， 最终导致剪切应力和剪切速率不满 足线性关系。于是提出了改进的宾汉姆模型。

　　式中： ∂γ/∂t 为速度梯度; c 为第二调整系数， Pa ·s2.

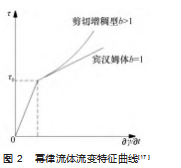
　　F.de Larrard 等[17]研究混凝土模型时发现剪切应力和剪 切 速 率 呈 非 线 性 关 系，提 出 了 标 准 的 Herschel-Bulkley 模型， 流变特征曲线如图 2 所示。

　　该 模 型 使 用 了 剪 切 应力、速度梯度、屈服应力 3个流变参数描述了自密实混凝土的流变特性：

　　式中： a 为一致性因素; b 为幂律指数。

　　Feys 等认为自密实混凝土的幂律指数通常大于 1. 表现为剪切增稠型， 用 H-B 模型描述自密实混凝土的流 变性更为准确。

　　2.2 混凝土流变性研究测试方法研究进展

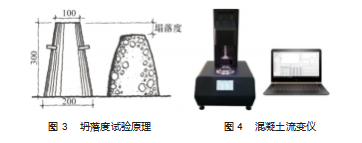
　　自密实混凝土的测试方法有很多， 最初的传统测试 方法是通过现场试验定性评估自密实混凝土的流变性， 比如坍落度试验 (图 3)、 V 型漏斗试验、 L 箱试验等。 它们都是通过控制自密实混凝土材料本身的性质来探究 自密实混凝土的流变性。其他的流变性研究测试方法还 有使用流变仪 (图 4)， 黏度计等或者通过理论流变学方 程来计算混凝土的塑性黏度和屈服应力值。这类方法统 称为定量预测。定性评估和定量预测是自密实混凝土流 变性测试方法的两大分类[18]。定性测试是通过相关的流 变实验来进行， 利用的仪器比较简便， 不论是在实验室 还是在施工现场都能进行， 但只能测试出自密实混凝土 的流变性能， 不能建立流变性与泵送过程中的流速、泵 压损失、物料比等参数的准确的函数关系。定量评估是 通过专业的流变性评估仪器来评判混凝土的流变性， 其 预测结果较为准确， 受外界影响较小， 比较精确， 还能 通过控制混凝土的相关参数来记录流变性的变化， 常用 来探究自密实混凝土泵送的规律。

　　3 CFD 自密实混凝土泵送数值模拟研究进展

　　数值模拟是利用计算机来做仿真试验， 通过计算机 控制不同参数模拟混凝土的泵送过程。通过数值模拟可 以比较直观地发现自密实混凝土的泵送规律。

　　1988 年 Tangawa 等[19] 最先采用有限单元法来模拟混 凝土泵送， 利用宾汉姆流变模型的粘塑性模拟了均一连 续介质状态的混凝土， 非均一连续的自密实混凝土则使 用宾汉姆模型的粘塑性悬浮单元法进行模拟。 1999 年， Puri 和 Uomoto[20] 提出更严谨的试验方法： 将混凝土视作 液固共存的多相材料使用离散单元法开展坍落度流变实 验和 V 型槽试验， 将砂浆视为外层粘结剂而粗骨料作为 球形颗粒单元的核心部分。 Roussel 等[21]基于宾汉姆流变 模型的三维结构的粘弹塑性模拟了新拌混凝土的流动， 同时做了相应的验证试验来相对照验证。 Thrane[22] 利用 了纳维斯托克斯方程中的伽辽金有限单元法公式模拟了 全尺寸自密实混凝土墙的浇筑试验， 并进行了带有钢筋 和无钢筋墙的 FIDAP 软件模拟。 Dufour[23] 等采用了带有 拉格朗日积分点的有限元方法(FEMLIP)， 将计算节点与 材料节点分开， 并将混凝土模拟成由砂浆和粗骨料构成 的非均质材料。

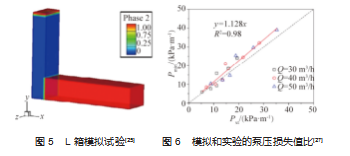
　　近年来， Feys 等发现 SCC 为剪切增稠型材料[15- 16]， 用幂律流体表示更为合适。杜新光等[24]采用拉格朗日有 限单元法， 使用流固耦合的方法分别对高性能混凝土和 自密实混凝土坍落度试验建立仿真模型并进行了模拟仿 真， 最后将试验数据与已有的文献对比验证。段化垒[25] 采用计算流体力学软件对新拌自密实混凝土坍落度试验、 L 箱试验 (图 5) 和 V 型箱试验进行了数值仿真， 通过控 制水灰比、减水剂、和砂浆率的参数来确定新拌混凝土 的工作性能。李靖祺和徐伟[26] 采用 CFD 中的多相流模 型， 基于有限体积法 (Volume of Fluid， VOF) 中的界面 追踪算法对自密实混凝土的流动进行仿真模拟， 并通过与 L 型箱试验对比验证 H-B 模型在进行 SCC 流动模拟上 的可行性。

　　李靖祺在前人的基础上采用了 H-B 模型对模板内的 自密实混凝土的流动进行了仿真模拟， 结合相关的流变 参数分析给自密实混凝土的泵送提供了较多的依据。同 时也做了宾汉姆模型的自密实混凝土在 L 箱的二维流变 实验， 结果表明宾汉姆模型的误差比自密 H-B 模型的平 均误差更大， H-B 模型更加适合作为自密实混凝土的流 变模型， 如图 6 所示。这可以从幂律流体流变特征曲线 做出很好的解释， 当指数为 1 时， H-B 模型可简化为宾 汉姆模型。同时， 使用 H-B 模型可以解决 SCC 在流变参数的回归分析中经常出现负屈服应力的问题， 提高流动 模拟中的稳定性和可靠性。

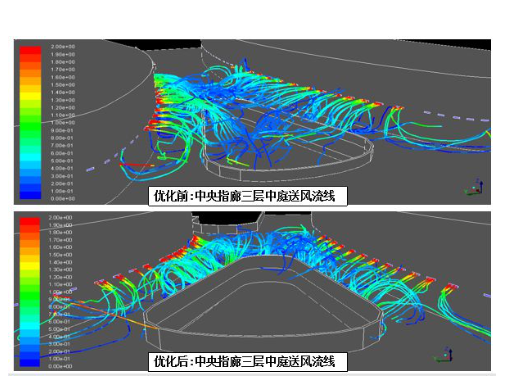
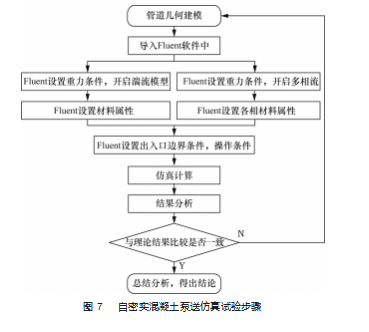
　　李悦[27] 将自密实混凝土视作连续体用 Fluent 软件建 立了新拌自密实混凝土流变性研究， 开展了自密实混凝 土在泵管中的泵送模拟实验， 如图 7 所示， 试验过程中 将自密实混凝土视作单相流和两相流分别给出相应的仿 真模拟， 探究了混凝土在泵送过程中的流速、压力分布、 单位压力损失的变化规律， 结果表明随着自密实混凝土 流速的增大， 自密实混凝土泵送过程中的沿程压力不断 增大， 管道中的单位压力损失呈增大趋势。魏子易[28]利 用 CFD 模拟了自密实混凝土在泵送过程， 分析了其中的 泵送压力损失及相关的流变规律， 并将模拟结果与实验 值进行对比， 结果表明， SST·k-ω湍流模型对自密实混 凝土的适应性很高， 能够准确预测混凝土泵送压力损失， 粘度是影响泵压损失的主要因素， 单位长度的泵压损失 与黏度成正比， 黏度越大， 混凝土由于剪切作用受到的 阻力越大， 导致泵压损失增大; 泵压损失随着屈服应力 的增大而减小， 且在混凝土屈服应力小于 150 Pa 时， 随着屈服应力的增大， 泵压损失降低程度更显著， 当屈服 应力大于 150 Pa 时， 其对泵压损失的影响不明显。

　　Sebastien Remond[29]利用 EDEM 软件设计了一种新的 模拟混凝土流动的 DEM 模型， 模型由硬芯和软壳模型组 成。相互作用基于传统用于颗粒流模拟的模型力， 硬芯 表示粗骨料接触时的相互作用。软壳表示相互作用时描 述粗骨料之间砂浆的剪切。软壳之间允许有较大的重叠， 从而得以计算骨料表面之间的近似剪切速率。然后， 考 虑砂浆的流变特性计算软壳之间的切向力。新拌混凝土 被描述为由两个同心球形颗粒组成的颗粒集合。内部球 体表示粗骨料; 外部球体表示一层砂浆与骨料一起移动。 新拌混凝土被描述为由代表粗骨料的球形硬颗粒组成的 复合颗粒的集合， 粗骨料被代表砂浆的同心球形层包围。 进行了两种模拟： 在 Couette 几何结构中进行的流变模拟 和坍落度试验模拟。流变模拟表明， 模拟混凝土的流变 行为可以用宾汉模型近似。所使用的力模型允许在混凝 土流变特性和模拟混凝土流变特性之间建立直接关系。 坍落度试验模拟 (图 8) 表明， 该模型能够描述混凝土 在流动过程中的形状。

　　Zigeng Wang 和 Ji Hao 等[30]考虑了欧拉方法和宾汉本 构关系， 以混凝土性能的测量值为输入参数， 模拟了超 高层建筑混凝土的水平盘管试验 (图 9) 和泵送试验。


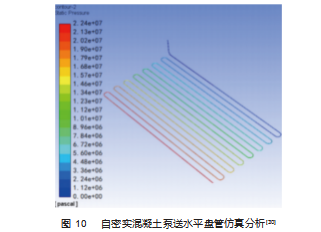
　　根据试验参数 CFD 欧拉模型和宾汉姆结构模型关系 能够准确描述混凝土在泵管中的流动行为。超高层建筑 混凝土水平盘管试验和泵送试验的模拟相对误差分别为 2.02% 和 2.72%。通过模拟结果可知， 混凝土在泵管中流 动时形成的润滑层厚度约为 2 mm， 这与混凝土配合比、 流变特性和泵送速度的相关性很低。随着距泵管进口距 离的增加， 润滑层的速度梯度逐渐减小。屈服层中混凝土的速度梯度逐渐增大， 屈服层的厚度也随之增大。塞 层中混凝土的流速增加， 但塞层厚度逐渐减小。混凝土 在水平管道中流动约 6 m 后趋于稳定， 此后这些指标没 有变化。自密实混凝土泵送水平盘管仿真如图 10 所示。


　　4 结束语

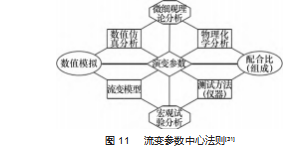
　　自密实混凝土是现代发展的进步的产物， 被称为近 几十年建筑性技术的革命性的发展， 具有广泛的应用前 景。本文从流变学的角度回顾新拌自密实混凝土工作性 研究。可以把研究工作归纳为新拌/自密实混凝土泵送规 律研究关系图 (流变参数中心法则， 如图 11 所示)。

　　自密实混凝土流变参数的研究是探究混凝土泵送规 律的核心， 从微观到宏观一步一步地探究分析， 以自密 实混凝土的组成、流变模型、物理化学分析等为基础， 数值模拟为方法来探究自密实混凝土的泵送规律， 这是 现代技术发展的趋势。

　　( 1) 流变模型的研究过程从宾汉姆模型、改进宾 汉姆模型、 H-B 模型发展到卡森模型， 未来的模型探 究发展方向需要仿真与验证的结合， 利用 CFD 来进行 仿真模拟， 采用试验数据进行佐证， 提出合适的自密 实混凝土流变模型。

　　( 2) 自密实混凝土泵送与自密实混凝土的流变性息 息相关， 流变性的测试方法可以分为定量测试和定性评 估， 分别适用于不同的场合。坍落度试验和漏斗试验等 适用于现场泵送时检测混凝土的工作性能。定量测试的 方法更适用于探究混凝土泵送的规律。

　　( 3) 自密实混凝土的微观状态模拟分析也是探究泵送 规律的一个重点， 微观状态下的自密实混凝土 DEM 模型更 容易确定混凝土的流动状态， 进而判断混凝土的可泵性。

　　( 4) 综合模拟仿真的结果， 黏度是决定自密实混凝 土泵送过程中泵压损失的一个重要因素， 单位长度的泵 压损失与黏度的关系成正比。


　　( 5) 研究自密实混凝土的泵送规律的研究很多， 从 传统的试验方法到现代的仿真模拟都有， 混凝土的泵送 规律研究已经比较成熟， 以后的发展应该着眼实际， 采 用计算机模拟进行辅助研究以节省人力物力， 成熟的计 算机技术可以为自密实混凝土的泵送提供了理论支撑。

　　参考文献：

　　[1] 余成行, 刘敬宇, 王磊 . C60 超高泵送混凝土的配制与施工[J]. 混凝土, 2008(6): 71-76.
　　[2] 张莉莉, 吴华, 黄天贵, 等 . 超高层混凝土泵送技术研究与应 用[J]. 建筑技术, 2015. 46(4): 341-344.
　　[3] 吴斌兴, 陈保钢, 徐建华, 等 . 高强高性能混凝土泵送压力损 失规分析[J]. 混凝土, 2011(1): 142- 144.
　　[4] 李立辉, 陈喜旺, 李路明, 等 . 自密实混凝土泵送压力变化规 律分析[J]. 施工技术, 2016. 45(12): 52-56.
　　[5] 余成行, 师卫科 . 泵送混凝土技术与超高泵送混凝土技术[J]. 商品混凝土, 2011(10): 29-34.
　　[6] 赵筠 . 混凝土泵送性能的影响因素与试验评价方法[J]. 江西 建材, 2014(12): 6-32
　　[7] 罗碧丹, 刘文利, 林伟才 . 混凝土泵送前后性能的对比试验研 究[J]. 混凝土, 2015(4): 123- 126.
　　[8] 阎培渝, 黎梦圆, 韩建国, 等 . 新拌混凝土可泵性的研究进展 [J]. 硅酸盐学报, 2018. 46(2): 239-246.
　　[9] Gonzalez-Taboada I, Gonzalez-Fonteboa B, Eiras- Lopez J, et al. Tools for the study of self-compacting recycled concrete fresh behaviour: Workability and rheology[J]. Journal of Cleaner Pro⁃ duction, 2017. 156(10): 1- 18.
　　[10] 李礼仁, 邓亚芬, 陈旭东 . 1 500 m 超远距离泵送混凝土性能 研究与应用[C]//第26 届华东六省一市土木建筑工程建造技 术交流会 . 杭州: 浙江省建设投资集团股份有限公司, 2010.
　　[11] Secrieru E, Fataei S, Schroefl C, et al. Study on concrete pumpa⁃ bility combining different laboratory tools and linkage to rheology [J]. Construction & Building Materials, 2017. 144(30): 451-461.
　　[12] Dimitri Feys, Ronny Verhoeven, Geert De Schutter. Steady- state rheological properties of fresh self compacting concrete and their evolution in time [J]. Annual Transactions of the Nor⁃ dic Rheology Society, 2007. 15: 35-41.
　　[13] Tattersall G H, Banfill P. The rheology of fresh concrete [M]. Pit⁃ man Advanced Publishing Program, 1983.
　　[14] Chong Hu, Francois de Larrard. The rheology of fresh high per⁃ formance concrete [J]. Cement and Concrete Research, 1996. 26 (2): 283-294.
　　[15] Dimitri Feys, Ronny Verhoeven, De Geert Schutter. Why is fresh self-compacting concrete shear thickening [J]. Cement and Concrete Research, 2009(39): 510-523.
　　[16] Dimitri Feys, Ronny Verhoeven, De Geert Schutter. Fresh self- compacting concrete, a shear thickening material [J]. Cement and Concrete Research, 2008(38): 920-929.
　　[17] De Larrard F, Ferraris C F, Sedran T. Fresh concrete: a hers⁃ cheI-bulkley material [J]. Materials and Structures, 1998(31): 494-498.
　　[18] 古川恭雄, 森博嗣, 黑川善幸 . 新拌混凝土流动与变形的模 拟方法研究[J]. 山东建材学院学报, 1998. 12(增刊1): 41-51.
　　[19] 邓熔 . 搅拌车中混凝土流变性研究及应用[D]. 湘潭: 湘潭大 学, 2016.
　　[20] Puri U C, Uomoto T. Characterization of distinct element model⁃ ing parameters for fresh concrete and its application in shotcrete simulations [J]. Journal of Materials in Civil Engineering, 2002. 32: 137- 144.
　　[21] Roussel N. Correlation between yield stress and slump: Compar⁃ ison between numerical simulation and concrete rheometers re ⁃ sults [J]. Materials and Structures, 2006. 39: 501-509.
　　[22] Lars Nyholm Thrane, Peter Szabo, Mette Geiker, et al. Simula⁃ tion of the test method ′L-box′ for self-compacting concrete [J]. Annual Transactions of the Nordic Rheology Society, 2004. 12: 47-54.
　　[23] Dufour, Gilles Pijaudier-Cabot. Numerical modeling of con⁃ crete flow: Homogenous approach [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009. 29: 395-416.
　　[24] 杜新光, 金先龙 陈向东 . 基于流固耦合的新拌混凝土流动及 变形仿真方法[J]. 上海交通大学学报, 2008. 42(12): 1993- 1996.
　　[25] 段化垒 . 自密实混凝土流动性试验的数值模拟[D]. 北京: 北 京交通大学, 2011.
　　[26] 李靖祺 , 徐伟 . 基于 Herschel-Bulkley 流变模型的自密实混 凝土流动的 CFD 模拟[J]. 工程力学, 2013. 30(1): 373-377.
　　[27] 李悦, 梅期威, 王子赓, 等 . 泵送混凝土在泵管中流动行为的 模拟研究[J]. 混凝土, 2019(12): 116- 119.
　　[28] 魏子易, 安晓鹏, 史才军, 等 . 基于 CFD 模拟的新拌混凝土泵 送压力损失预测[J]. 材料导报, 2019. 33(22): 3738-3743.
　　[29] Sebastien Remond, Patrick Pizette. A DEM hard-core soft- shell model for the simulation of concrete fl ow[J] cement and Concrete Research, 2014(58): 169- 178.
　　[30] Zigeng Wang, Ji Hao, Yue Li, et al. Simulation of Concrete pumped in horizontal coil and super high-rise building based on CFD [J]. Journal of Advanced Concrete Technology Vol . 20. 328-341.
　　[31] 单智 , 石建军 , 熊恩 , 等 . 新拌自密实混凝土流变性研究[J]. 混凝土, 2010 (11): 108- 112.
 
 
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/59411.html