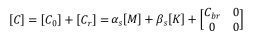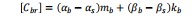SCI论文(www.lunwensci.com)
摘要:本文依托MATLAB软件结合高阶动力算法——积分求微法编制了计算程序,首先对一栋基底隔震结构进行了特定地震波作用下结构动力响应时程分析;其次对该结构非隔震设计情形采用MATLAB编程计算,对比两者在相同地震作用下的动力响应;最后将本文算法与其他方法计算结论对比。以上计算均取得了较为满意的结果,验证了该程序算法在实际工程中的适用性。
关键词:MATLAB;基底隔震;动力响应;高阶算法
Response Analysis of Isolated Structure based on MATLAB
Sun Lei,Shi Xixi,Feng Fei,Gao Jikai,Ye Ziyan
(Nanjing Vocational College of Science and Technology,Nanjing Jiangsu,210048)
Abstract:In this paper,a calculation program is developed based on the MATLAB software combined with the high-order dynamic algorithm-integration and differentiation method.Firstly,the time-history analysis of the dynamic response of a base-isolated structure under the action of a specific seismic wave is carried out;secondly,the non-isolated design of the structure is calculated by MATLAB programming,and the dynamic responses of the two under the same earthquake are compared;finally,the algorithm in this paper Compared with the calculation results of other methods;the above calculations have achieved relatively satisfactory results,which verifies the applicability of the program algorithm in practical engineering.
Key words:MATLAB;base isolation;dynamic response;high-order algorithm
一、前言
基底隔震原理是通过在建筑物上部结构与基础之间设置隔震层的方式来隔离地震波带来的能量,常见的房屋底部隔震层由橡胶隔震支座和阻尼器等部件组成。与传统抗震结构体系相比,基底隔震方案不仅可以使结构内部免遭地震冲击的破坏,而且改变了传统抗震的设计施工思路。
结构动力响应分析是认识动态系统性态和行为的基础性工作。积分求微法是一种高效的结构动力分析算法[1]。结合该原理,依托MATLAB软件编制算法程序,可经过一步计算便同时获得精度较高的时段内每个时步的全部动态响应。
二、多自由度体系隔震计算
隔震体系的计算立足于以下基本假定。
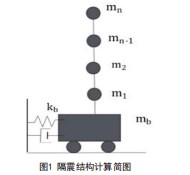
第一,隔震体系由上部结构和隔震层两部分组成,将钢筋混凝土结构、隔震层顶部的梁板结构作为其上部结构的一部分进行计算和设计。第二,上部结构处于线弹性状态,结构层间刚度可按D值法计算而得,计算时应考虑结构的非比例阻尼性质。第三,采用离散化的层间剪切模型,将质量近似集中到各楼层。将隔震层作为第一个质点,使上部各层质点化,并将整个结构的竖向承重构件合并成一个总的竖向杆件,从而形成悬臂串联质点模型。第四,只考虑单向水平地震的作用,同时将房屋刚度中心与质量中心重合,在水平地震的作用下结构不会产生绕竖轴的扭转,如图1。
该体系在地震作用下的运动方程可表达为常见的形式:

式中,g为地面运动加速度时程;M、C和K分别为体系的质量、阻尼和刚度矩阵。为各质点相对于地面的位移向量。
由于上部结构和隔震系统具有明显不同的阻尼,引用分区瑞雷阻尼模型[2],可将阻尼矩阵表示为:
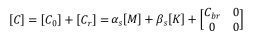
式中,Cr为体现隔震结构非比例阻尼的余项阻尼矩阵:
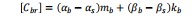
其中kb、mb分别为隔震系统的等效刚度和隔震层质量,αs、βs为上部结构的瑞雷阻尼比例系数。
积分求微算法在待求时段中划分出了多个相邻等距时步,以精细积分法结合秦九韶算法,同时逆用微分求积原理求解含有矩阵指数卷积的数值计算,从而得到体系各时刻的动力响应。本文采用MATLAB程序基于多自由度阻尼体系运动时程积分求微法算法进行计算。
算法简要步骤及部分代码如下所示,该算法的稳定性、精度及计算效率均在文献中有更为详细的讨论和验证[3]。
 三、钢筋混凝土框架结构隔震分析
三、钢筋混凝土框架结构隔震分析
(一)计算模型参数及地震波的选用
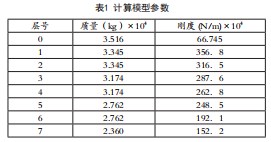
以文献中给出的钢筋混凝土建筑结构为分析目标,底部采用橡胶垫隔震技术,各层层高均为3.6m。以本文前述为假设条件,可将各层质量和刚度参数表示为表1所示内容。需要说明的是,表1中的0代表隔震层,故结构非隔震设计情形下的计算可以将表1中0层信息直接删除[4]。
选取典型的地震地面加速度时程进行记录,计算相应动力响应,一方面可作为使用本文方法的阐释,另一方面可考察该方法的可靠性和有效性。地震波采样用1940年美国加州帝王谷地震中El Centro 9号台测得的南北向地震纪录,采样周期为0.02s,本次分析时间取8s。
(二)计算结果对比分析
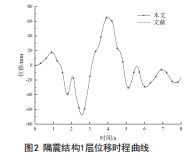
本文采用积分求微算法,时间步长dt取值0.08s,时间分段数m取值4,然后进行隔震结构1层位移时程的计算。其结果和文献传统算法计算的结果如图2所示。
从图2可以看出,在相同地震波(El Centro)作用下的同样隔震结构,当时间步长dt取值0.08s、时间分段数m取值4时,平均步距为0.02s的计算结果和文献中用传统算法得到结合几近一致。
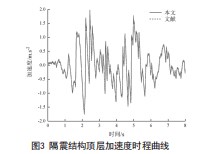
图3为两种方法下的结构顶层加速度时程曲线。本文算法与文献传统算法计算出的加速度时程曲线几乎一致。图3表示隔震结构顶层7层的加速度峰值为1.924m/s2出现在2.45s。这充分表明基础隔震层对于地震波的能量起到了阻隔作用,在减小传至上部结构的加速度的同时减小了层间剪力。
(三)隔震与非隔震结构动力响应分析
基于前述动力响应积分求微原理的算法程序,可分析地震作用下上述7层钢筋混凝土结构隔震与非隔震设计情形下的不同响应情况。考虑到当时步长度一定时,使用文本算法编制的程序的计算精度会受时步内插入节点数量的影响,即节点的数量越多计算结果越精确,故程序中的两个重要参数,即时步长度dt与时步分段数m分别为0.04和4。
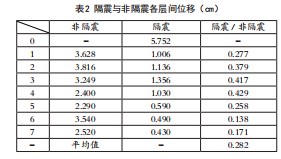
运行程序可直接得到隔震前后各层位移和加速度的时程曲线,对非隔震和隔震建筑各层层间位移进行分析和数据处理,可得隔震与非隔震结构层间的比较,如表2所示。
可以看出,在水平地震的作用下,基础隔震体系的变形主要集中在隔震层,其层间位移达5.752cm。上部结构变形很小,隔震后建筑第1层层间位移是非隔震结构第1层的0.277,顶层层间位移减小至隔震设计前的17.1%,隔震与非隔震层间位移比值平均为0.282,基础隔震设计使得隔震效果得到发挥。为了表达得更形象,现通过图4显示隔震与非隔震设计的显著效果。
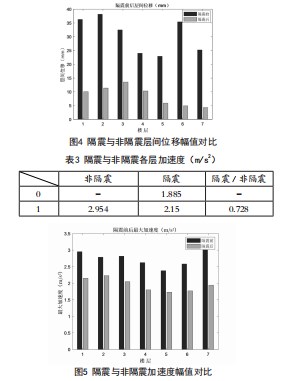
对隔震和非隔震建筑各层加速度进行分析和数据处理,可得隔震与非隔震结构层的加速度幅值比较,如表3所示。
表3显示隔震结构与非隔震结构各层加速度幅值的变化情况。对于基础隔震结构,可看出上部结构各层加速度与非隔震结构相比平均可降至71.4%,尤其是顶层加速度,减小至非隔震结构顶层加速度的64.6%,减震效率达到28.6%,基础隔震设计效果明显。为表达得更形象,现通过图5显示隔震与非隔震设计的显著效果。
可以看出,基于MATLAB运用积分求微算法可以快速进行隔震结构的地震分析,同时可以将计算结果更形象、更直观地呈现出来,便于分析建筑物的地震反应,也验证了该程序算法在实际工程中的适用性。
四、结语
第一,本文建筑隔震体系采用剪切型结构模型。对隔震结构动力响应而言,由于隔震层和上部结构在材料特性上存在差异,非比例阻尼特性不可忽略,故建立非比例阻尼模型结构进行动力响应分析。
第二,本文依托MATLAB软件结合高阶动力算法——积分求微法编制了计算程序,应用于钢筋混凝土框架隔震结构的地震响应分析。编制积分求微算法的关键在于对DQ原理的逆用,利用该方法可快速求得各时段内多个时刻上的动力响应值,且准确高效。
第三,建立结构基础隔震设计前后的计算模型,采用MATLAB编制高阶算法程序分别进行动力响应计算。从结果来看,基础隔震设计起到了阻隔地震能量向上部结构传输的目的,隔震效果显著。
第四,将基础隔震结构的计算结果以可视化方式展示其在地震作用下的动力响应时程,结合与其他文献的比较可看出本文方法的高效性和适用性。
基于MATLAB程序编制积分求微算法进行基础隔震结构时程的分析计算,能够取得令人满意的结果,这为今后处理类似工程问题提出了一个极具潜力并值得开发利用的方法。
【参考文献】
[1]李鸿晶,梅雨辰,任永亮.一种结构动力时程分析的积分求微方法[J].力学学报,2019(5).
[2]R.克拉夫,J.彭津.结构动力学(第二版)[M].北京:高等教育出版社,2006.11.
[3]李鸿晶,杨筱朋,梅雨辰.一种多自由度阻尼体系动力问题的高阶分析方法[J].工程力学,2021.38(01).
[4]曾兆江,尹颖.MATLAB在建筑结构减振工程中的应用[J].工程地质计算机应用,2010(4).
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/51689.html