密钥动态选择机制的图像加密算法（附论文PDF版下载）

SCI论文（www.lunwensci.com）:
 
特别说明：理工类、计算机类和医药类等论文在小编发布时可能会因为复杂的科学计算公式，导致文本格式出错，在阅读时较难读懂，阅读体验一般，建议大家可以直接在文章底部翻页到最后一页下载论文PDF版文档进行深度学习和阅读，感谢理解！

朱淑芹，刘荣月，周冉冉，王文宏
ZHU Shuqin, LIU Rongyue, ZHOU Ranran, WANG Wenhong
聊城大学 计算机学院，山东 聊城 252059
School of Computer Science, Liaocheng University, Liaocheng, Shandong 252059, China

ZHU Shuqin, LIU Rongyue, ZHOU Ranran, et al. A new image encryption algorithm based on key dynamic selection mechanism. Computer Engineering and Applications

Abstract: In this paper, a six dimensional discrete chaotic system is constructed, and a pseudorandom number generator is designed based on the six dimensional discrete chaotic system. Based on the pseudorandom number generator, an image encryption scheme with key dynamic selection mechanism is proposed. The encryption scheme adopts the classic scrambling-diffusion encryption structure. In this encryption scheme, the scrambling sequence is related to the sum of the pixels of the plaintext image, The diffusion key stream in the diffusion stage is dynamically changing according to the pixel value, so the algorithm can resist the attack of chosen plaintext. In decryption, the decryption key is only the initial value of the chaotic system, and the sum of the pixels of the plaintext image is not needed, In this way, the difficulty of key management in "one time pad" encryption  scheme (encryption of different images with different keys) is overcome. The experimental results and security analysis show that the algorithm has the advantages of large key space, no obvious statistical characteristics of ciphertext, sensitive to plaintext and key, and able to resist differential attacks and chosen plaintext attack. It has good application prospects.

Keywords：Six dimensional hyperchaos；Image encryption; Scrambling-diffusion; Key dynamic selection mechanism; Chosen plaintext attack

摘 要：本文构造了一个六维离散混沌系统，并在此混沌系统的基础上设计了一个伪随机数生成器。基于该伪随机数生成器提出了一种密钥动态选择机制的图像加密方案。该加密方案采用了经典的置乱-扩散加密结构。在该加密方案中，置乱序列与明文图像的像素总和相关，而在扩散阶段的扩散密钥流是根据每个像素值动态变化的，因此算法能抵抗选择明文（密文）的攻击。解密时的密钥只是混沌系统的初始值，明文图像的像素的总和是不需要的，因此克服了“一次一密”加密方案（加密不同明文所用密钥不同）中密钥管理的难度。实验结果和安全性分析表明：该算法具有密钥空间大、密文没有明显的统计特性、密文对明文和密钥非常敏感、能够抵抗差分攻击和选择明（密）文的攻击等优点，具有良好应用前景。

关键词：六维超混沌；图像加密；置乱-扩散；密钥动态选择机制；选择明文的攻击

基金项目：山东省自然科学基金 (Grant. ZR2017MEM019)、聊城大学自然科学基金(No.318011606)；国家级大学生创新创业训练计划项目（No.201710447064）。

作者简介：朱淑芹 (1979－)，女，讲师，硕士，主要研究方向为混沌理论、图像处理；刘荣月(1997-)，女，聊城大学计算机学院电子商务专业学生；周冉冉(1997-)，女，聊城大学计算机学院电子商务专业学生；王文宏 (1973-), 男, 博士, 副教授,  主要研究方向为图像处理、模式识别、机器视觉。

1 引言
随着计算机和通信技术的迅速发展，多媒体信息，如图像、音频、视频，由于其清晰、生动、形象的优点已经成为网络信息的主要载体，得到广泛应用和传播。图像总是涉及商业、军事、医疗和政治等敏感事件，如何确保在公共网络上传输和存储的图像的安全性引起了密码学和信息安全领域前所未有的关注。与文本数据不同的是，图像数据具有数据量大、冗余度高的特点。若用传统的加密算法,如 DES、AES 会导致加密效率低、密文样本统计性差的缺点。同时由于像素相关性强，传统的加密算法加密出的密文图像能反应出明文图像的大体轮廓。另外，图像允许一定程度的失真，与文本相比，它不那么敏感。因此传统的加密算法不再适用于图像加密[1]。

混沌理论的发展为图像加密开辟了一个新的道路。混沌是一种确定的非线性系统产生的复杂的、看似随机的物理现象，其产生的序列具有伪随机性，非周期性及对控制参数和初始条件的高度敏感性，同时混沌序列能够大量快速产生和准确再生， 这些特性使得混沌系统特别适用于图像加密。自从1998 年 Fridrich[2]提出了具有开创性的替代-扩散加密体系结构以来，学者们先后提出了许多基于混沌系统的图像加密算法。这些算法中大部分都是基于图像像素的置乱和像素扩散的加密思想[3-9]，例如， 文献[4]提出一种通过行、列两轮置乱，再进行扩散运算的新的彩色图像加密算法。谢国波、王朝阳[8]提出了基于滑块与矩阵旋转的混沌图像加密算法，该算法得创新之处是根据密钥序列的数值，旋转明文图像不同位置的子矩阵块来进行明文图像的置乱处理。Lu xu et al[9]提出了一种基于块置乱和动态索引扩散的混沌图像加密算法，该算法采用了传统的置乱-扩散加密体系结构，但在扩散阶段采用了动态索引的密文反馈机制和动态索引的明文反馈机制，以抵抗选择明文的攻击，这是该文的最大创新之处。

有些算法还结合了 DNA 编码的思想[10-14]。例如，Aqeel-ur-Rehman  et  al[13]提出了基于DNA 编码的混合像素间替换的图像加密算法。该算法的主要特点是在扩散阶段采用了混合像素间替换的扩散方法，具有加密效率高的优点。田海江等人[14]以时空混沌模型作为核心控制方程，设计了一种动态 DNA 编码的图像加密算法。该算法的新颖之处是打破了以前算法中采用固定编码的模式，采用动态编码机制，这就加强了系统的安全性。然而， 很多基于混沌的数字图像加密算法是不安全的，尤其不能抵抗选择明文/密文的攻击[15-19]。朱淑芹[15] 等通过选择多幅明文图像攻击，破解了一种基于比特置乱的超混沌图像加密算法；Zhu et al [16]通过选择明文攻击结合选择密文攻击的方式破解出一种具有密文反馈机制的混沌图像加密算法，使得利用密文反馈机制来抵抗选择明文攻击的方法失效；文献[17]通过选择明文攻击破解了一种基于像素置乱和比特替换的混沌图像加密算法。在破解过程中，不是破解出加密时的密钥序列，而是通过像素值全为零的图像的密文图像与待解密的密文图像作异或运算，恢复出待求明文图像置乱后的序列，使得原算法的比特位替换操作失效。

文献[19]通过选择明文图像攻击的方法，破解了一种基于三维位矩阵置换的图像加密方案。可以看出这些算法被破解的主要原因是加密系统所用密钥流与待加密图像无关，即加密任何图像所用密钥是固定不变的，这就使得加密系统不能抵抗选择明文/密文攻击，为了抵抗选择明文/密文的攻击，近年来提出了各种各样的与明文相关“一次一密”的密钥流生成方案 [3、12、20-23]。例如，文献[12]使混沌系统的初始值与明文图像的像素总和相关。文献[3、17]把图像的哈希值作为混沌系统初值的一部分，这样混沌系统产生的随机序列与明文相关，增强了加密系统的安全性。而文献[18]不但把图像的哈希值作为混沌系统初值的一部分，还用图像的哈希值生成一个掩模图像与明文图像进行异或运算，这进一步加强了安全性。这样，加密系统的密钥集就是混沌系统的初值和图像的哈希值(像素总和)。同样，解密时，不但用到混沌系统的初始值，还要用图像的哈希值(像素总和)。

解密不同的密文就需要不同的哈希值(像素总和)，这为密钥管理增加了难度，在实际应用中是不可行的。为此，本文提出一种具有密钥动态选择机制的图像加密算法。本算法利用混沌系统生成多个随机序列，根据像素值的不同，选择不同的随机序列进行加密，这样加密不同的图像所用密钥序列不同，算法能抵抗选择明文/密文攻击。另外，该算法的密钥集就是混沌系统的初始值，加密不同的图像所用加密密钥是不变的，不像文献文献[3、17、18] 那样把图像的哈希值作为密钥的一部分，解密不同的图像时需传递相应的图像哈希值。减少了密钥管理的难度。

混沌密码体制的安全问题主要分为两大类：一是由加密算法的结构造成的。二是由混沌系统自身所造成，由于计算机计算精度的限制，混沌系统在数字域中有动力学退化的现象，也就是产生的混沌随机数序列随机性能差。一般来说，超混沌系统具有两个及两个以上的正的 Lyapunov 指数、动力学行为更加复杂，产生的混沌序列随机性更强，因此用超混沌进行图像加密，其安全性更高。最近，文献[24]构造了一个四维离散超混沌系统。在文献[24] 的基础上，本文首先构造了一个六维离散混沌系统，然后采用新构造的六维超混沌来进行加密方案的设计。

2 六维离散混沌系统的构造与仿真

文献[24]构造的四维离散混沌系统的形式如式(1)
 x1 i sinx1 i1sinx1 i 1 x3 i 1 x1 i1 x2 i 1;

献[17]通过选择明文攻击破解了一种基于像素置乱
和比特替换的混沌图像加密算法。在破解过程中，

 x2 i sinx2 i1sinx1 i 1;
 x i sinx i 1sinx i 1 x i1;

(1)

不是破解出加密时的密钥序列，而是通过像素值全为零的图像的密文图像与待解密的密文图像作异或运算，恢复出待求明文图像置乱后的序列，使得原算法的比特位替换操作失效。文献[19]通过选择明文图像攻击的方法，破解了一种基于三维位矩阵置换的图像加密方案。可以看出这些算法被破解的主要原因是加密系统所用密钥流与待加密图像无

  3 1 1 3
 x i 2sinx i1 x i 1;
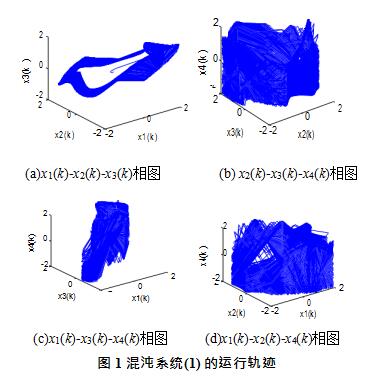
采用 wolf 方法计算的系统(1)的最大李亚普诺夫指数为 λLE1=0.2543 。给定初始值 X(0)={0.9654 ，
0.0546，0.6705，0.78546}，混沌系统(1)的运动轨迹如图 1 所示。


本文在式(1)基础上通过反馈控制和增加状态变量 x5、x6 构造出的六维离散混沌系统具有如下式
(2)的形式
 x1 i sinx6 i 1 sinx1 i 1 x3 i 1  x1 i 1  x2 i 1; x i sinx i 1sinx i 1;

3 基于六维离散混沌系统的伪随机数生成器的设计
设置好混沌系统(2)的初值，生成六个混沌序列 xt={xt(k)｜k=1, 2, 3 ,…, t=1, 2, 3, 4, 5, 6}，利用序列 xi，xj，xq 按照式(3)生成序列密钥 Ti,j,q，这里 i，
j，q 各不相等，且 i，j，q∈{1, 2, 3, 4, 5, 6}，这样
就生成 C 3=20 个不同的序列 T 。(i, j, q 按从小到

  2 3 2

(2) 6

i,j,q

 x i sinx i 1 sinx i 1 x i 1;

大排列)

  3 5 4 3

 x i  2sinx i 1  x i 1;

255 2L(X (k) min(X ))

(3)

  4 5 1

Ti, j,q (X (k))  mod(round( ), 256)

x5 i sinx4 i 1sinx6 i 1;
 x6 i  cosx2 i 1  x6 i 1sinx5 i 1;

max(X ) min(X )
其中

X (k)  k x (k)  k x k  x (k), k  3, k 

5; L  1010 ;

1   i 2    j q 1 2

采用 wolf 方法计算的系统(2)的最大李亚普诺夫指
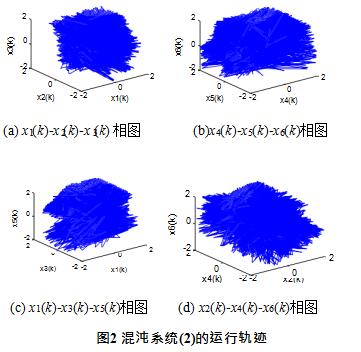
数为 λLE1=0.6104。系统(2)的最大李亚普诺夫指数大于系统(1)的最大李亚普诺夫指数，因此混沌系统(2) 具有更加复杂的动力学行为。 给定初始值X(0)={0.9654, 0.0546, 0.6705, 0, 0.78546,  0.1854}，
混沌系统(2)的运动轨迹如图 2 所示。

min(X )  min{X (k) | k 1, 2,..., mn}；
max( X )  max{X (k ) | k  1, 2,..., mn}；
round(a)表示对数 a 四舍五入取整。混沌系统的初始值作为随机数生成器的种子，混沌系统的初始值不同，就得到不同的 20 个随机数序列 T,i,j,q。这 20
个随机序列就形成如表 1 所示的 10 对随机序列对。
加密不同位置的像素就从表 1 中选择不同的随机序列对，这就是密钥动态选择机制的原理。

表 1   密钥流动态选择表
序列 0 1 2 3 4 5 6 7 8 9
Key1 T1,2,3 T1,2,4 T1,2,5 T1,2,6 T1,3,4 T1,3,5 T1,3,6 T1,4,5 T1,4,6 T1,5,6
Key2 T2,3,4 T2,3,5 T2,3,6 T2,4,5 T2,4,6 T2,5,6 T3,4,5 T3,4,6 T3,5,6 T4,5,6

4 加密算法

加密算法包括混沌随机数随机性能分析和具体的加密方案。随机数的性能好坏在很大程度上决定了混沌密码体制的安全性，因此,在加密之前要先对随机数生成器的性能进行分析。而随机数好坏的关键指标是随机性、均匀分布性等特性。
4.1
混沌伪随机数生成器的性能分析
取初始值 x1(0)=0.9654 ， x2(0)=0.0546 ，
x3(0)=0.6705，x4(0)=0，x5(0)=0.78546，x6(0)=0.1854。
按照3.1章节生成随机数的方法，迭代混沌系统(2)
30000次，得到20个{0,1, 2,…,255}的随机序列Ti,j,q， 同 时 对 初 始 值 进 行 轻 微 的 扰 动 取x1(0)=0.9654+10-15 ，其它初始值保持不变， 迭代

30000次，得到另一20个{0, 1, 2, …, 255}的随机序
列Si,j,q。对随机序列Ti,j,q和Si,j,q进行NIST SP 800-22 检测、信息熵分析，以验证生成的随机数的均匀性、复杂性和随机性。
4.1.1SP800-22的伪随机性检测
目前世界上应用比较广泛的随机数检测标准是
NISTSP800-22标准，NISTSP800-22有16项指标测
试，测试前设定显著性水平，每项的测试结果均转换为p值进行判断，若测试结果中p值均大于显著性

水平a，则认为测试对象满足SP800-22的随机性要求。
对于长度为30000的的20个随机序列Ti,j,q和20 个随机序列Si,j,q，分别转换为长度为240000的二进制序列，取显著性水平a=0.05，进行NISTSP800-22 的16项指标测试，结果如表2所示，表2列出了它们各自的最大值、最小值和平均值。测试结果中p值均大于显著性水平a，表明测试满足SP800-22的随机性要求。

表 2 随机序列 Ti,j,q 和 Si,j,q 的 NISTSP800-22 标准检测
测试项   P-value
随机序列Tijq 随机序列Sijq
max min average max min average
频率测试 0.54943 0.54109 0.54573 0.59001 0.54706 0.56707
块内频率测试 0.62987 0.60044 0.60746 0.59876 0.52007 0.56098
累积和测试orward 0.40896 0.36997 0.38949 0.46654 0.42654 0.44454
累积和测试everse 0.68432 0.64787 0.66408 0.57398 0.54099 0.56098
游程检测 0.36489 0.32476 0.34431 0.38709 0.33674 0.36787
块内最长连续“1”测试 0.25829 0.23127 0.24968 0.29208 0.19293 0.25099
二元矩阵秩测试 0.58793 0.56345 0.57315 0.55940 0.48654 0.50987
离散傅里叶变换测 0.18023 0.14053 0.16208 0.25098 0.22190 0.24239
非重叠模版匹配测 0.45015 0.42087 0.43982 0.50987 0.43987 0.48226
重叠模版匹配测试 0.48865 0.45096 0.45899 0.57459 0.49899 0.55899
全局通用统计测试 0.46386 0.43898 0.45366 0.48762 0.43387 0.46457
近似熵检测 0.38761 0.33786 0.35765 0.39089 0.32109 0.36096
随机偏移测试 0.46908 0.42988 0.44765 0.43987 0.33987 0.39097
随机偏移变量测试 0.29152 0.27182 0.29005 0.36091 0.30654 0.34098
线性复杂度检测 0.69128 0.65234 0.67094 0.55354 0.48547 0.52097
串行测试 0.37909 0.33986 0.35607 0.30943 0.27893 0.28865

4.1.2信息熵分析
信息熵是用于表征信源的不确定性程度的概念。信息熵的计算公式为式(4)

息熵越大，表明序列的随机性越好，经计算 20 个
序列 Ti,j,q 中的的信息熵的最大值、最小值和平均值分别为 7.9978bit、7.9477bit 和 7.9965 bit，而 20 个序列 Si,j,q 中的的信息熵的最大值、最小值和平均值分别为 7.9956bit、7.9377bit 和 7.9935 bit，非常接近理想值。图 3(a)和图 3(b)分别是随机序列 T1,2,3、S1,2,3 的数值分布曲线。图中横坐标代表{0，1，…，255} 中的 256 个数，纵坐标代表密钥流中取{ 0，1，…，
255}中每个数的频数。可以看出随机序列 T1,2,3、
S1,2,3 分布均匀，伪随机性良好。

(a)随机序列 T1,2,3 的 (b)随机序列 S1,2,3 的分布曲线  分布曲线。
图 3 随机序列均匀性检测
4.2加密算法
假设明文图像是一个具有 256 级灰度、大小为
l=m×n 的图像，将其转化为一维向量 P={p(1), p(2), p(3), …, p(mn)}，加密过程包括两个阶段：置乱阶段和扩散阶段。具体步骤如下：
(1)给定初始值 X(0)={0.9654,  0.0546,  0.6705,
0.9876, 0.78546, 0.1854}，迭代超混沌系统(2)生成长度为 l 的六个混沌序列 xi (i=1，2，3，4，5，6)。

然后利用式(3)生成 20 个{ 0, 1, …,  255}上的序列
Ti,j,k。
(2)像素位置置乱阶段的操作就是对图像像素位置进行全局置乱，以打破相邻像素的相关性。根据下面的式(5)和式(6)置乱图像序列P，在生成置乱序列时加入了一个与明文相关的扰动项g， (g=sum(P)/(256l)

为密钥集的一部分，加密不同的图像就要传递相应的明文图像的哈希值或像素总和。该算法的加密系统的密钥集就是混沌系统的初始值，加密不同的图像密钥集是不变的。因此，减少了密钥管理的难度。

5解密算法

hi i mod[ floor(x (i)g1014) ,l i] temp  P(i), p(i)  P(h(i)), P(h(i))  temp i=1, 2, 3, …, l

(5)
(6)

任何完美的加密算法都应被拥有正确密钥者解密，即算法是可逆的。否则，这样的加密算法是没有意义的。解密过程是加密过程的逆过程具体步骤如下：

由式(5)可以看出置乱序列h(i)的生成与明文图像像
素总和相关，加密不同的明文图像所用置乱序列h(i) 不同，这样可以使算法抵抗选择明文的攻击。
(3)扩散阶段将实现对像素位置全局置乱后的图像P进行像素值替代加密，以混淆密文与明文之
(1)
与加密算法中的步骤(1)完全一样，根据给定的混沌系统初始值，迭代超混沌系统(2)生成长度为
l 的六个混沌序列 xi (i=1，2，3，4，5，6)。然后利用式(3)生成 20 个{ 0, 1, …, 255}上的序列 Ti,j,k。
(2)由式(7) 可知 vp(l)=0 ，从而由式(8) 知

间的关系。在扩散阶段首先要生成序列SP，根据SP

s p l  

0 。由 sp(l)进一步知道 Key1(l)和 Key2(l)，

的不同来决定选择不同的密钥流。为了产生“明文
不同，密钥流不同”的效果，按式(7)计算序列
VP={vp(1), vp(2), vp(3),…, vp(l)}

根据密文像素 c(l-1)和 x3(l)，利用式(10)计算出 Q(l),
从而可以解密出 p(l)
(12)


v p i   




j  2


p  j , i f i  1;

(7)

pl   cl   key2 l   (mod((cl 1  key1 l ), 256)) Qi
(3)解出了 P(l)，由式(7)可知 vp(l-1)=P(l)，由式

 v p i  1   p i  , i f i  2 , 3 , . . .l .

(8)进一步可以得到

对序列VP进行(8)式的操作，得到序列SP={ sp(1),
sp(2), sp(3),…, sp(l) }, sp(i)∈[0,9]，i=1, 2, 3, …, l。

s p l 1  floor  mod  p l  x2 l 1 1012 ,10 




(13)

  2565 

  v p i  x (i ) 

  (8)

  

s p i  

floor  mod 

2  1012 ,10  



  256  
从式(7)和式(8)可以看出密钥流的选择和明文图像的每一个像素值都有关。根据sp(i)从上面的表1中选择不同的密钥流对步骤(2)中置乱后的明文序列p(i) 进行扩散操作。例如sp(1)=7，则Key1(1)=T1,4,5(1)，
Key2(1)=T3,4,6(1)。就用T1,4,5(1)和T3,4,6(1)对p(1)进行
扩散操作。为进一步加强算法对明文敏感的效果， 先利用式(10)生成一个与密文相关的用于对密文进行扩散的序列Q。最终的密文扩散公式为下面的式(9)-(11)，这样得到密文序列C={c(1), c(2), c(3), …,
c(l)}。再把C转化为m×n的矩阵，即得密文图像。

由 sp(l-1)进一步知道 Key1(l-1)和 Key2(l-1)，且根据
密文像素 c(l-2)和 x3(l-1)，利用式(10)计算出 Q(l-1)， 从而可以解密出 p(l-1)。依次类推，分别解密出p(l-2)，p(l-3)，…，p(2)，再计算出 vp(1)，从而计算出 Key1(1)、Key2(1)和 c(0)、Q(1)，最后解密出 p(1)。
(4)进行置乱的反变换。由于置乱前后图像的所有像素值的总和不变，因此步骤(3)解密出的置乱图像 P 的所有像素总和就等于明文图像的像素总和， 进而计算出 g 值，因此在解密时，不需要明文图像的像素和。由(5)式可得置乱序列 H={h(1), h(2),
h(3), …, h(l)}。需注意的是进行置乱变换的反变换

c(0)   floor(mod(v p 1 x  11012  / 2565 , 256))
Q(i)  mod [ floor ( x (i)  c(i  1)) 1014 ) , 256]
ci  pi Key2 i (mod((ci 1 Key1i),256))Qi

(9)
(10)
(11)

时，是 从最后一个像素到第一个像素进行式(6)的操作。

从式(8)可以看出 sp(i)的生成与明文像素值有关，因此加密不同的图像所用的密钥流 Key1 和 Key2 不同。而从式(10)可以看出随机序列 Q(i)的生成与密文相关，因此加密不同的明文图像生成的序列
Q(i)不同。再结合式(11)可以看出我们的算法具有加密不同的图像所用密钥流不同的特点。所以算法可以抵抗选择明文的攻击。另外，本算法并不像文献
[18]那样把明文图像的哈希值或图象的像素总和作

6实验仿真与安全性分析

6.1加密算法实验仿真
在本算法的仿真过程中，选择 206×345 的
“autumn”图像进行实验，加密系统的密钥集为混沌系统的初始值，设置为X(0)={0.9654, 0.0546, 0.6705,
0.5698, 0.78546, 0.1854}。仿真结果如图4所示，其中图4(a)为原明文图像，(b)为置乱后的图像，(c)为密文图像。从图4(c)中看不出明文图像的任何信息。

(a)为原明文图像 (b)为置乱后的图像 (c)为密文图像
图 4 实验仿真结果

算法的有效性。为节省篇幅，只呈现“cameraman” 原图像的直方图、加密后图像的直方图，分别如图
5 的(a)-(b)，从统计直方图看出，原图像的直方图呈现双峰分布，统计特性明显。而加密图像的直方图中各像素值的概率分布都接近等概率分布，因此加密后的图像是一幅随机图像。

6.2安全性分析
为了评估算法的总体性能，下面分别从算法的密钥空间、 密文统计分布特性、 抗差分攻击和抗选择明(密)文攻击等方面对算法的总体性能进行评估。
6.2.1 密钥空间分析
加密时可用的所有密钥数就是密钥空间的大小，密钥空间越大，抵抗蛮力攻击的性能越好。本算法的密钥集为keys={x1(0), x2(0), x3(0), x4(0), x5(0),
x6(0)}。实验验证x1(0), x2(0), x3(0), x4(0), x5(0), x6(0)

256个灰度级

的精度可达10-15，x6(0)的精度可达10-14。密钥空间可达1015×1015×1015×1015×1015×1014=1089≈2296。这么
大的密钥空间远远大于文献[1]中指出的一个安全的密码系统的密钥空间应大于2100，因此我们的算法对蛮力攻击是安全的。
6.2.2统计特性分析
本文的加密方案采用了密钥动态选择机制，密钥流的选择与像素值有关。从密文图像直方图呈均匀分布、密文图像相邻像素相关性很小、密文图像的信息熵接近于 8bit 可以看出所得密文图像是一幅随机图像，从而明文图像的统计特性完全被打破，隐藏了明文图像的信息。下面就从以上几个方面进行具体分析。
(1)统计直方图
直方图揭示了图像像素的分布规律，是数字图

(a)“cameraman”的明文图像 (b)密文图像的直方图
的直方图
图 5 加密前后的直方图对比
(2)像素相关性分析
对一幅自然图像来说，相邻像素非常接近，即具有很强的相关性，图像信息的冗余度很大。而图像加密的目标之一就是祛除这种冗余性，减小相邻像素的相关性。对于要评估的明文图像和密文图像，分别随机地选取4000个像素点作为参考点，以这些点为基准分别沿水平方向、垂直方向和对角线方向取其相邻的像素点与之构成像素对，利用相关系数公式(14)来分别计算明文图像和对应的密文图像在这三个方向的相关系数值，所得原图像和加密图像的相邻元素的相关系数如表3

像的一个基本属性。密文图像的直方图应完全不同



n n n

(14)

于明文图像的直方图，且密文图像直方图分布越均


xc 

n 
i  1

x i   y i     
i  1

x i    y i            i  1

n     n  2 n

    n  2

匀，加密效果越好。在一幅直方图中，横坐标代表

n 
i  1

x  2         
  i  1

x i 


n 
i  1

y   2         
  i  1

y i 


灰度图像的 256 个灰度级，纵坐标代表图像所有像素取每个灰度级的频数。本文加密了四幅经典图像
“autumn”、 “pepper”、“rice”、“cameraman”来表明

其中，xi，yi分别表示相邻两个像素的灰度值，
n表示选取的像素对的个数。

表 3  原图像和加密图像的相邻元素的相关系数对比
图像 水平方向 垂直方向 对角方向
“Rice”明文图像 0.9427 0.9263 0.8994
“Rice”密文图像 -0.0026 0.0127 -0.0261
“Cameraman”明文图像 0.9588 0.9360 0.9095
“Cameraman”密文图像 -0.0027 -0.0209 0.0014
“autumn”明文图像 0.9675 0.9845 0.9821
“autumn”密文图像 -0.0056 0.0132 0.0109
“pepper”明文图像 0.9894 0.9931 0.9847
“pepper”密文图像 -0.0031 0.0174 -0.0187

为了更形象、直观地比较图像加密前后的相邻像素的相关性，我们以“cameraman”为例，分别绘制出其明文图像和对应的密文图像在这三个方向的相关性分布图。图6和图7分别为“cameraman” 明文图像和对应的密文图像在三个方向的相关性

分布图。其中图6(a) 为“cameraman”明文图像的水平方向相关分析图，图6(b) 为明文图像的垂直方向相关分析图，图6(c) 为“cameraman”明文图像的对角方向相关分析图。图7(a) 为“cameraman”密文图像的水平方向相关分析图，图7(b) 为“cameraman”

密文图像的垂直方向相关分析图，图7(c)  为
“cameraman”密文图像的对角方向相关分析图。从



E   
i  1


p i l o g 2 (


p i )

(15)

表3和图6及图7可以看出，明文图像的相邻像素间在三个方向上具有很强的线性关系，而密文图像的相邻像素间在三个方向上关系呈现随机的对应关系，祛除了像素的冗余性和相关性。

其中，pi 为第 i 阶灰度值出现的概率。对于 256 级
灰度图像来说，n=256。当密文的概率分布为等概率分布时，即取[0，255]之间每一个值概率均为
1/256 时，具有最大熵为 8bit。本文加密的“rice”、
“cameraman”、 “autumn”、 “pepper” 四幅数字

图像的信息熵如表 4 所示,可以看出四幅图像的密文图像的信息熵都非常接近 8bit。表明加密后图像的随机性、不可预测性很高。
表 4    加密图像的信息熵

图像 密文的信息熵 图像 密文的信息熵

rice 7.9956 autumn    7.9964

   cameraman    7.9945 pepper     7.9975


6.2.3
密钥敏感性分析
一个安全的加密算法应该对密钥敏感，这样才能抵抗蛮力攻击。密钥敏感性体现在两方面：一方

pixel value on location(x,y) pixel value on location(x,y) pixel value on location(x,y)
(a)水平方向相关 (b)垂直方向相关 (c)对角方向相关分析 分析 分析
图 6 明文图像的相关性分布图

面，用具有微小差别的两个不同的密钥加密同一幅明文图像时，得到的对应的两幅密文图像将完全不同，这一点可以用密文图像的改变率t 衡量。另一方面，当解密时，若输入与正确密钥有微小差别的错


误解密密钥，从解密结果中得不到明文图像的任何有用的信息。计算密文图像的改变率t 的具体方法如下：计算密钥a的敏感性时，用密钥a加密明文得到密文图像C1，用密钥a+h（其他密钥不变）加密得到密文图像C2，用密钥a-h加密得到C3，则C2与C1灰度值不同的像素数Num1占整个图像的比例和C3与C1 灰度值不同的像素Num2占整个图像的比例取均值， 得到t，即t=0.5*( Num1/m*n+Num2/m*n)，其中m×n 表示图像的大小。以此方法计算出各密钥的敏感

pixel value on location(x,y) pixel value on location(x,y) pixel value on location(x,y)

(a)水平方向相关 (b)垂直方向相关 (c)对角方向相关分析 分析 分析
图 7 密文图像的相关性分布图
(3)密文图像信息熵分析
在信息论中，熵是表征对象运动状态有序程度的一个量，熵越大，表明对象的无序程度越高。在图像中，可以根据图像的各个像素点的灰度分布的有序性来定义图像的信息熵。图像越混乱，图像信息熵越大，图像提供的信息量就越少。信息熵的计算公式为(15)

性，以加密图像“autumn”为例，我们计算出的各个密钥对应的图像的改变率如表5所示。计算的结果表明算法对密钥具有很强的敏感性。计算中密钥
x1(0)，x2(0)，x3(0)，x4(0)，x5(0)的改变量h均是10-15，
x6(0)改变量h是10-14。
   表5   各初始值的敏感性测试   密钥  x(0) y(0) z(0) w(0)

敏感性t 0.9946 0.9899 0.9967 0.9978

下面的图8中a～f 分别为密钥集是表6中的各密钥时的解密图像，可以看出在解密图像中得不到原图像的任何信息。这也进一步说明了算法对密钥的高度敏感性。

表 6   解密时所用错误密钥
各密钥 x1(0) x2(0) x3(0) x4(0) x5(0) x6(0)
Keys1 0.9654+10-15 0.0546 0.6705 0.5698 0.78546 0.1854
Keys2 0.9654 0.0546+10-15 0.6705 0.5698 0.78546 0.1854
Keys3 0.9654 0.0546 0.6705+10-15 0.5698 0.78546 0.1854
Keys4 0.9654 0.0546 0.6705 0.5698+10-15 0.78546 0.1854
Keys5 0.9654 0.0546 0.6705 0.5698 0.78546+10-15 0.1854
Keys6 0.9654 0.0546 0.6705 0.5698 0.78546, 0.1854+10-14

  D i j 

(16)

N    P   C   R 

i  1
M

j  1
N

 1 0 0 %

   M      N      
     

 i 1 j  1 

25 5  

(17)


(a)Keys1解密结果 (b) Keys2解密结果 (c) Keys3解密结果

(d) Keys4解密结果 (e) Keys5解密结果 (f) Keys6解密结果图8 错误密钥解密出的图像

差分攻击是通过比较分析有特定区别的明文在通过加密后的变化传播情况来攻击密码算法的一种攻击方式。可以用数字图像像素变化率(NPCR) 和归一化平均变化强度(UACI)来衡量数字图像加密算法抗击差分攻击的能力。NPCR和UACI的计算公式[3]分别为式(16)、(17)

UA CI       1 00%
M   N
其中M×N为图像的大小。c(i, j)为原密文图像在(i, j)处的像素值，c′(i, j)为明文改变后对应的密文图像在(i, j)处的像素值。对于8位灰度图像，NPCR与
UACI的理想期望值分别为：NPCRE  =99.6094%，
UACIE=33.4635% 。本算法中随机选取每幅图像中
200个像素点，改变它们的像素值，结果计算的
NPCR值最大值，最小值，平均值以及UACI值最大值，最小值，平均值都列在表7中。它们都非常接近理想值。可见，原图像中一个像素灰度值的变化会导致加密图像中几乎所有像素灰度值发生变化。从而验证了该算法对明文敏感，具有很好的抗差分攻击性能力。

表7 算法明文图像微小改变的NPCＲ和UACI测试结果

Images  NPCR%  UACI%
Max Min Average Max Min Average
Rice 99.8634 99.6626 99.7062 33.4569 33.3916 33.4819
autumn 99.6932 99.5221 99.6315 33.6754 33.4508 33.6569
pepper 99.9532 99.3839 99.6656 33.8543 33.4619 33.6418
camera 99.7898 99.4668 99.5657 33.6492 33.2858 33.3578

6.2.4选择明文（密文）攻击分析
选择明文和选择密文攻击是密码分析中两种有效且应用广泛的安全攻击方法。前者假定攻击者有机会临时获得加密机的使用机会，于是他(她)可以选择一些特殊的明文，并得到相应的密文；后者假定攻击者有机会临时获得解密机的使用机会，于是他(她)可以选择一些特殊的密文，并得到相应的明文；然后可以由这些明－密文对推导出等价的中间密钥。许多成功的密码攻击案例都采用的是选择明文（密文）攻击方式。本文提出的加密方案能够抵抗选择明文（密文）攻击，这体现在两个方面：一是在置乱阶段，置乱序列的生成与明文图像的像素总和有关，即加密不同的图像所用置乱序列不同。二是在像素扩散阶段，扩散密钥流与明文图像的每个象素值和密文像素值都相关，这样加密不同的图像所用扩散密钥流不同。

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jisuanjilunwen/445.html