5 实验结果与分析
5.1 实验内容
本文实施以下几个对比实验:
(21)
(22)
相似度算法中又包括了 5 种局部相似度指标算法
[CN,Jaccard, PA, AA, RA][6],2 种路径相似度指标算法[LP, Katz][6] , 3 种随机游走相似度指标算法
[RWR,ACT,Cos][6];8 种网络嵌入算法中包括了 6 种基于矩阵分解的算法[NMF,SVD,LAP,HOPE,LLE], 一种随机游走算法 Node2Vec 以及一种深度学习算法 SDNE。各算法预测 MAP 指标与时间消耗如表 2 所示(时间单位:秒)。基本参数设置如下,网络嵌
(1)与常用的链路预测算法在时间耗费与预测
精度上的对比。一般来说预测精度是首要评价指标, 其次是时间耗费。通过该实验可以直接评价模型的好坏。
(2)对比不同的表征维度对不同路网预测精度的影响。不同的表征维度对实验结果也会产生影响, 我们希望增加该实验来找出合适的表征维度。
(3)不同梯度下降算法对 loss 函数的影响。梯度下降算法对找到 loss 函数的极值以及在优化模型的效率上有着重要的意义,我们希望能够找到合适的梯度下降算法对模型进行训练。
(4)自动编码器的层数对预测精度的影响。通过构建多层网络模型,研究网络的层数对预测结果的影响,便于最优的网络层次选择。
(5)路网网络嵌入的二维可视化效果。我们希望了解模型在进行表征学习时,模型学到了什么样特征,通过将节点映射到平面空间,从而可以直观
入算法表征维度都为 128,迭代次数均为 50 次。图 5 为各算法的平均 MAP 预测指标,图 6 为
各算法的平均时间耗费,从图 5 和图 6 中我们可以 看出在基于相似度算法中,基于路径相似度的 Katz 算法与基于随机游走相似度的 ACT、Cos 算法取得了不错的效果,但是在时间耗费上,ACT 与 Cos 的时间耗费较多。在基于网络嵌入技术的算法中,深 度学习模型如 SDNE、KAENE 所耗费的时间是其他网络表征模型的几倍或几十倍,其原因主要在于深 度学习的迭代机制以及多层神经网络的参数过多导 致的。在预测精确度上,KAENE 取得了最高的平均 MAP 指标,同时它也是耗时最多算法。SVD 在小数据集中取得了不错的效果,同时它是耗时最少 的网络表征模型,全局精确度最差的算法是 Jaccard, 全局耗时最少的算法是 PA(优先连接指标)算法。
表 2 链路预测算法时间耗费与预测精度表 s
HengYang ChangSha HangZhou Rockford Seattle SanFrancisco
Method Time MAP Time MAP Time MAP Time MAP Time MAP Time MAP
CN 0.598 0.150 28.216 0.158 211.551 0.155 22.232 0.161 103.216 0.166 229.172 0.151
Jaccard 0.393 0.153 27.649 0.156 321.805 0.154 22.944 0.160 86.054 0.165 239.904 0.147
PA 0.669 0.253 27.053 0.245 138.337 0.240 22.588 0.230 73.224 0.239 136.183 0.216
AA 0.446 0.153 28.376 0.161 329.088 0.158 22.646 0.165 108.973 0.167 303.026 0.153
RA 0.409 0.155 27.081 0.162 304.336 0.159 21.718 0.166 107.413 0.167 296.361 0.154
LP 1.289 0.224 91.129 0.224 1299.226 0.228 74.183 0.233 386.289 0.222 1130.770 0.201
Katz 5.457 0.272 53.008 0.264 500.587 0.262 51.473 0.256 233.878 0.263 514.554 0.230
RWR 7.674 0.198 73.553 0.211 1017.762 0.211 62.314 0.215 351.615 0.197 744.623 0.173
ACT 7.803 0.272 759.828 0.271 10577.082 0.267 534.125 0.257 2779.629 0.264 9434.607 0.251
Cos 4.584 0.268 794.242 0.250 9705.852 0.248 517.142 0.269 3511.995 0.245 8761.833 0.243
NMF 32.639 0.361 1302.549 0.356 6500.033 0.350 1183.974 0.327 3450.774 0.350 7259.661 0.308
SVD 1.438 0.650 65.607 0.463 387.730 0.382 55.179 0.439 196.515 0.426 407.642 0.362
GF 8.662 0.333 132.432 0.314 539.370 0.308 118.519 0.291 324.221 0.310 581.470 0.265
HOPE 3.013 0.576 88.405 0.426 482.998 0.388 76.742 0.403 257.071 0.400 533.500 0.343
LAP 9.646 0.619 398.847 0.537 2089.411 0.495 420.597 0.484 1355.974 0.521 2365.255 0.428
LLE 7.368 0.638 414.252 0.586 3401.714 0.562 536.283 0.516 3297.191 0.572 3914.500 0.490
Node2vec 6.110 0.434 134.158 0.507 689.923 0.464 129.721 0.420 361.078 0.475 755.138 0.415
SDNE 2006.504 0.534 8008.310 0.508 20229.245 0.505 12027.505 0.523 13569.462 0.507 20355.337 0.408
KAENE 2966.766 0.643 9775.685 0.554 26665.995 0.583 13322.652 0.506 15224.112 0.577 26554.688 0.517
图 5 各算法平均 MAP 指标 图 6 各算法平均耗时
图 7 HengYang 路网不同表征维度时预测精度 图 8 ChangSha 路网不同表征维度时预测精度
5.3不同表征维度对算法的影响
为了探索不同表征维度对预测结果的影响,本文选取了ChangSha 与HengYang 两个城市的路网数据集。一般来说,网络表征的维度通常为2n且2n €
|V|,n 为自然数且大于 0。
图 7 中由于节点数量为 726,因此只能嵌入到
512 维。对比图 7 与图 8 我们可以发现随着维度的不断增加,预测精度值形成了正态分布,因此,我们在选择表征维度参数时一般不会选择太小或太大。
另外一个发现是,随着数据集网络节点数量的不断增加,最优表征维度也在提高,比如 HengYang 数据集(|V|=726 )的最优网络表征维度为 32,而
ChangSha 数据集(|V|=5018)的最优网络表征维度为 64。
5.4梯度下降算法对 loss 的影响
对损失函数进行梯度下降时所使用梯度下降算法的选择也非常重要,本文对比了 SGD、Adam、
Adadelta、RMSprop、Nadam、Adagrad、Adamax 7
种梯度下降算法在ChangSha 路网数据集中的表现, 梯度下降算法相关参数均使用默认参数,模型迭代次数为 50 次。实验结果如图 9 所示。从图中可以看出使用 Adam 算法取得了最快的下降效果及最小的
loss 值,因此效果最好。而 SGD 算法刚开始虽然取得不错的下降效果,但是随着迭代次数的增加,其不稳定性开始体现出来,使得 loss 值跳出了极小值范围,最终进入了 loss 值很高的平稳状态,因此效果最差。其他 5 种算法刚开始都处于平稳下降状态, 最后随着迭代次数的增加都逼近了极小值,因此效果一般。本文中,我们选用了 Adam 梯度下降算法。
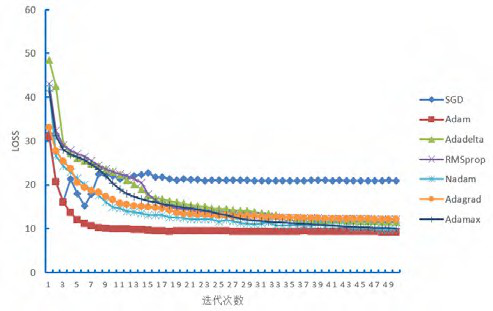
图 9 梯度下降算法对损失函数的影响
5.5自动编码器的层数对预测精度的影响
为了探究自动编码器层数对预测精度的影响, 本文设计了自动编码器层数与预测结果的对比实验, 实验选取了 HengYang 作为实验数据集,相关参数设置如下:初始表征维度为 512,每层表征维度呈等差数列递减,最终表征维度为 128,迭代次数均为 50 次。实验结果如图 10 所示,从图中可以看出随着层数的增加,MAP 指标一开始整体呈现上升趋势,在达到 40 层以后,MAP 指标开始下降,说明此时模型泛化能力开始下降。
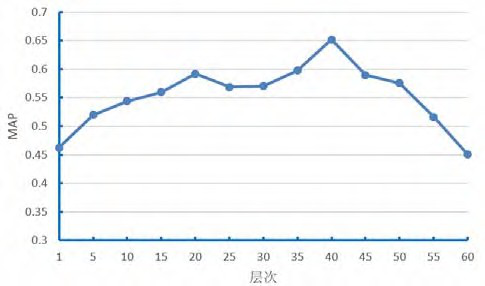
图 10 自动编码器层数对预测精确度的影响
5.6模型可视化效果
由于路网的节点数量较多,在二维平面上展示时,导致大部分节点都重叠在了一起。因此,在本次实验中,我们仍选用了图 1(a)中的复杂网络图。此外,我们对比了[NMF, SVD, GF, HOPE, LLE ,
Node2vec, SDNE]七种网络嵌入模型在该数据集上可视化的表现(注:本次实验 KAENE 无法添加 L 限制)。如图 11 所示,从网络拓扑结构上看 LLE 与
KAENE 与图 1(a)更相近,而 SDNE 则更倾向于学习到了网络的“二阶近似”特性,即具有共同邻居的两个节点之间具有相似性,因为它将节点[4,5] 聚集到了一起。
(a)NMF (b) SVD
(c)GF (d) HOPE
(e)LLE (f) Node2vec
(g)SDNE (h)KAENE
图 11 网络表征可视化效果
6结束语
本文从路网链路预测的应用背景出发,结合深度学习的思想,提出了基于 KAENE 的路网链路预测模型。实验结果表明,KAENE 取得了良好的表现。虽然,KAENE 在预测精度上较高,但是其逐层训练机制与高迭代次数,往往使得模型需要耗费大量的训练时间,对于海量的路网数据来说,需要更多的计算资源和内存空间,对于一些 GIS 研究机构来说,是不可接受的。因此,寻求更加高效的链路预测算法或者实现模型的并行计算将会是本文后续要解决的问题。
参考文献:
[1]Zhao F, Sun H, Wu J, et al. Analysis of road network pat- tern considering population distribution and central busi- ness district[J]. PloS One, 2016, 11(3): e0151676.
[2]Zhao Y, Wu Y J, Levina E, et al. Link prediction for par- tially observed networks[J]. Journal of Computational and Graphical Statistics, 2017.
[3]宋海权, 郭进, 刘刚. 基于复杂网络的城市道路重要度评价及路网自动综合方法[J]. 测绘工程, 2017, 26(1): 8-12.
[4]赵国锋, 苑少伟, 慈玉生. 城市路网的复杂网络特性和鲁棒性研究[J]. 公路交通科技, 2016, 33(1):119-124.
[5]Goyal P, Ferrara E. Graph Embedding Techniques, Ap- plications, and Performance: A Survey[J]. Knowledge-Based Systems, 2018.
[6]吕琳媛. 复杂网络链路预测[J]. 电子科技大学学报, 2010, 39(5):651-661.
[7]Belkin M, Niyogi P. Laplacian eigenmaps and spectral techniques for embedding and clustering[C] Advances in Neural Information Processing Systems. 2002: 585-591.
[8]Grover A, Leskovec J. node2vec: Scalable feature learn- ing for networks[C] Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Dis- covery and Data Mining. ACM, 2016: 855-864.
[9]Wang D, Cui P, Zhu W. Structural Deep Network Embed- ding[C] ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2016: 1225-1234.
[10]Ahmed A, Shervashidze N, Narayanamurthy S, et al. Dis- tributed large-scale natural graph factorization[C] Pro- ceedings of the 22nd International Conference on World Wide Web. ACM, 2013: 37-48.
[11]Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323-2326.
[12]Lee D. Learning the parts of objects with nonnegative matrix factorization[J]. Nature, 1999, 401(6755):788.
[13]Dan K. A Singularly Valuable Decomposition: The SVD of a Matrix[J]. College Mathematics Journal, 1996, 27(1):2-23.
[14]Ou M, Cui P, Pei J, et al. Asymmetric Transitivity Pre- serving Graph Embedding[C] KDD. 2016: 1105-1114.
[15]Hinton G E, Salakhutdinov R R. Reducing the dimen- sionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507.
[16]Hinton G E, Srivastava N, Krizhevsky A, et al. Improving neural networks by preventing co-adaptation of feature detectors[J]. Computer Science, 2012, 3(4):págs. 212-223.
[17]Bengio Y, Lamblin P, Dan P, et al. Greedy layer-wise training of deep networks[C]// International Conference on Neural Information Processing Systems. MIT Press, 2007:153-160.
[18]Rumelhart D E, Hinton G E, Williams R J. Learning rep- resentations by back-propagating errors[J]. Nature, 1986, 323(6088): 533.
[19]Hinton G E. A practical guide to training restricted Boltzmann machines[M] Neural Networks: Tricks of the Trade. Springer, Berlin, Heidelberg, 2012: 599-619.
[20]Chang S, Han W, Tang J, et al. Heterogeneous Network Embedding via Deep Architectures[C] ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2015:119-128.
[21]Katz L. A new status index derived from sociometric analysis[J]. Psychometrika, 1953, 18(1): 39-43.
[22]Zakzeski J, Bruijnincx PCA, Jongerius AL, et al. The cat- alytic valorization of lignin for the production of renewa- ble chemicals[J]. Chemical Reviews, 2010, 110(6): 3552-3599.
[23]Haklay M, Weber P. OpenStreetMap: User-Generated Street Maps[J]. IEEE Pervasive Computing, 2008, 7(4):12-18.
[24]赵玲, 邓敏, 王佳璆,等. 应用复杂网络理论的城市路网可靠性分析[J]. 测绘科学, 2013, 38(3):64-68.
[25]Kunegis J. Konect: thekoblenz network collection[C]
Proceedings of the 22nd International Conference on World Wide Web. ACM, 2013: 1343-1350.
《基于 Katz 自动编码器的城市路网链路预测模型》附论文PDF版下载:
http://www.lunwensci.com/uploadfile/2018/0811/20180811045032291.pdf
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/440.html


