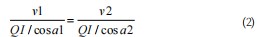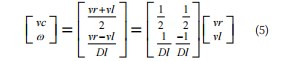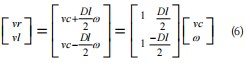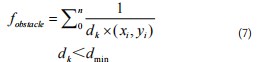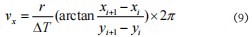SCI论文（www.lunwensci.com）:
摘要：在四轮差速机器人自主运行的过程中,为了更好的完成任务要求,需要加入一个实时的检测,当机器人遇到障碍物时根据需要对路径进行调整,以避开障碍物,所以这就需要加入局部路径规划的算法。Time-Elastic-Band(TEB)算法所规划的局部路径在规避障碍物时不能完全符合机器人的运动状态,因此需对原算法进行优化,并基于ROS平台对优化后的算法进行仿真测试,最终得到符合机器人实际运动状态的局部路径。
关键词：四轮差速机器人；局部路径规划；优化TEB算法；ROS
Local Path Planning of Four-wheel Differential Robot Based on Optimized TEB Algorithm
CHEN Xi,SHI Boqiang,GUO Hui
(Shunde Graduate School,University of Science and Technology Beijing,Beijing 100083)
【Abstract】：In the process of autonomous operation of four-wheel differential robot,in order to better complete the task requirements,a real-time detection needs to be added.When the robot encounters obstacles,the path should be adjusted as needed to avoid obstacles,so it needs to add the algorithm of local path planning.The local path planned by Time-Elastic-Band(TEB)algorithm cannot fully meet the motion state of the robot when avoiding obstacles.Therefore,the original algorithm needs to be optimized,and the optimized algorithm is tested based on ROS platform,andfinally the local path in line with the actual motion state of the robot is obtained.
【Key words】：four-wheel differential robot;local path planning;improved algorithm of TEB;ROS
近年来随着我国制造业的迅速发展和“中国制造2035”的提出,移动机器人也得到了迅速发展,而自主导航又是人工智能领域研究的重点,移动机器人的功能不仅仅是能够按照预定的路线运行,还要具有一定的自主避障能力,以完成在复杂环境中的工作。因此,机器人需要能够根据当前的工作环境实时规划出一条局部路径,以规避预定路线上的障碍物。目前常用的局部路径规划算法Time-Elastic-Band(TEB)算法,加入了对时间信息的计算,还综合考虑到了机器人的运动学特征,因此对不同类型的机器人都有一定适应性。但是在实际运用中,机器人规避障碍物时局部路径会不符合运动状态,规划出来的路径不够平滑的问题。对此,国内外学者基于不同运动形态的机器人对传统TEB算法做出了一些优化改进。
文献[1]中,作者基于阿克曼转向的机器人模型,在传统TEB算法的基础上对速度约束进行优化,即使在阿克曼转向机器人在避障转弯时速度发生震荡,也能对其进行一定约束,从而使机器人运动的更平滑。文献[2]中,作者对传统TEB算法加入障碍膨胀化处理进行优化,能有效增加机器人和障碍物直接的缓冲区,即使机器人在行驶的过程中发生震荡也能有效减少冲击,以保障机器人运行的安全。在上述文章中,缺乏对TEB算法规划的局部路径的优化。
根据上述文章分析,本文基于四轮差速机器人[3]模型对TEB算法进一步优化。在原有的算法基础上,通过对局部路径的路径点进行处理,使用二次样条插值法对路径点进行重新拟合,使规划出的局部路径更加平滑,更加符合四轮差速机器人的运动状态,最后在ROS[4,5]平台上进行仿真验证。
1 TEB四轮差速机器人运动模型构建
1.1机器人运动分析
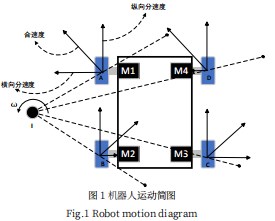
首先针对四轮差速机器人构建机器人运动模型其结构简图如图1所示。纵向分速度[6],其结构简图如图1所示。
由图1可以看出,当机器人的四个主动轮电机转速不同时,根据速度合成则会绕中心的I产生角速度ω,即可实现转向。
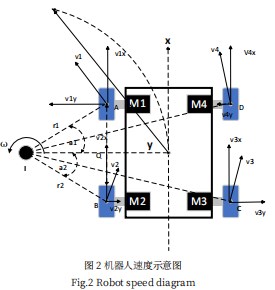
如图2所示,左侧两个车辆与的角速度ω可表示如式(1)所示：
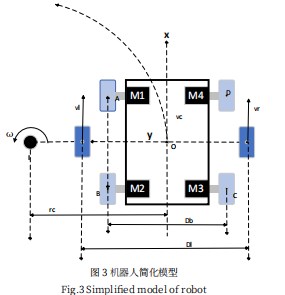
式中v1和v2分别表示左前轮和左后轮的线速度,r1和r2分别表示其对应的转弯半径。在ΔAQI和ΔBQI中,使用三角函数进行转换,可表示为如式(2)所示：
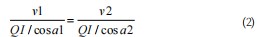
式中a1和a2分别表示∠AIQ和∠BIQ,对上式进行化简得如式(3)所示：
v1x=v1cosa1=v2x=v2cosa2 (3)
同理分析右前轮和右后轮可得如式(4)所示：
V4x=v4cosa4=v3x=v3cosa3 (4)
式中a4和a3分别表示∠DIQ和∠CIQ
1.2四轮差速机器人模型简化及构建
通过上述计算得,同一横向的两个轮子速度相同,因此可把四轮差速简化成两轮差速进行建立运动学模型,如图3所示。
以等效模型来建立运动模型,简化后的运动模型中心o的速度和角速度可表示为如式(5)所示：
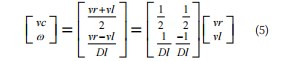
通过对中心o的速度进行分解计算可得出等效左右轮的速度,以此建立运动学模型如如式(6)所示：
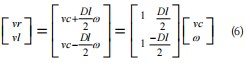2 TEB算法的构建及优化
2.1 TEB算法模型的构建
TEB算法在运行时,会将机器人的位姿坐标信息拟合成一个带有时间信息的elastic band。i时刻机器人的位姿坐标为Si=[xi,yi,θi],xi为横坐标,yi为纵坐标,θi为机器人偏转角度。∆Ti为机器人的位姿Si到位姿Si+1之间间隔的时间。TEB算法的轨迹位姿点如图4所示。
TEB算法的核心部分在于对障碍物的规避。首先通过机器人上的激光雷达可以测得每一时刻机器人距离障碍物的实际距离dk,机器人与障碍物之间的期望距离为dmin。在机器人处于某个位姿时,激光雷达反射同一个障碍物的不同部分都会有一定的信息,所以一般会受到n个来自障碍物的影响因子。当障碍物与机器人之间的距离大于dmin时,则判定机器人不需要进行避障,约束值fobstacle记为0。当机器人与障碍物之间的距离小于期
望距离时,则需要进行避障,通过计算约束值fobstacle来进行矫正,如式(7)所示:
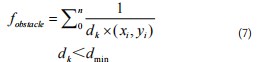
TEB局部路径规划算法的核心思想是根据时间间隔,计算出每一个间隔点时机器人的位姿,并且将计算出的位姿点存入一个二维数组。在进行避障时,机器人应优先考虑局部目标点,这些目标点取决于计算出的位姿点,而不是全局路径上的位姿点。在构建TEB算法模型时,首先需要计算每个位姿点的约束值总和f(T),i(T)为每个位姿的约束值,γk为每个位姿对应的权重),如式(8)所示：
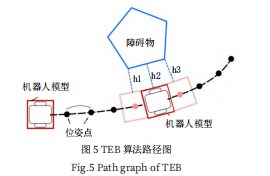
TEB算法的中文译名为时间弹性带算法,顾名思义即根据时间间隔计算出位姿点,然后根据每个位姿点的总约束值对原有路径进行弹性拉伸,使路径绕开障碍物,以达到避障的目的,如图5所示。
TEB算法在对原有的路径进行弹性变形之后,机器人的运动轨迹也会跟着发生相应的改变,因此不能根据原来的线速度和角速度进行行驶,需要重新计算线速度和角速度。线速度vx由位姿坐标(xi,yi)和时间间隔∆T通过如式(9)所示求得：
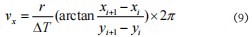
角速度vy由位姿角θi通过如式(10)所示求得：
2.2 TEB算法的优化
2.2.1融合路径点
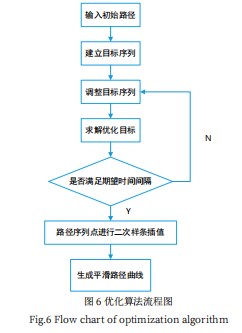
TEB算法是用来进行局部路径规划的,因此需要具有实时性、准确性和迅速性。但是每一段局部路径的位姿点较多,每个都计算的话不仅浪费时间而且可能导致输出滞后,甚至出现较大的误差。所以为了提高TEB算法的效率和准确性,需要适当的调整相邻两个位姿点的时间间隔并减少需要计算的位姿点。当位姿点的个数减少时,路径的圆滑度也会下降,这里采用样条插值法进行优化[7],优化算法流程如图6所示。
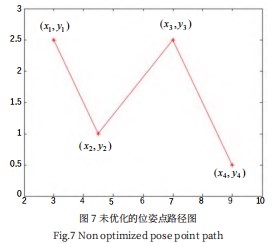
在进行样条插值法优化之前首先需要定义一个二维数组,用来储存调整减少之后的位姿点,设每个位姿点为(xi,yi),然后将每两个相邻的位姿点的连线进行弹性优化,使其路径更加平滑。未优化的位姿点路径如图7所示。
这样直接连起来的直线显然不能够作为路径,因此需要使用样条插值法会将任意两个位姿点拟合成一个平滑曲线函数,最简单的曲线函数就是二次函数,设函数表达式y(x)如式(11)所示。
y(x)=a+bx+cx2(11)
式中x⊆(xi,xi+1)的a、b和c为满足该函数条件的代求系数,这里取上图四个位姿点为例。四个点可以分为三个区间,每一个区间的曲线都对应一个二次函数,因此需要确定三组a、b、c也就是九个待定系数,下面就是根据条件找出九个方程组进行未知数的求解:
(1)首先每相邻的两条曲线在区间端点处的函数值是必须要相等的,所以在点x2处函数一的值等于函数二的值,在点x3处函数二的值等于函数三的值带入式(11)求得如式(12)所示：
y1(x2)=a1+b1x2+c1x
y2(x2)=a2+b2x2+c2x2
y2(x3)=a2+b2x3+c2x3
y3(x3)=a3+b3x3+c3x3
y1(x2)=y2(x2)
y3(x3)=y3(x3)
(2)将第一个端点带入函数一,第四个端点带入函数四,由式(11)求得如式(13)所示：
y1(x1)=a1+b1x1+c1x
y3(x4)=a3+b3x4+c3x
(3)函数一和函数二在点x2处的一阶导的导数值相等,函数二和函数三在点x3处的一阶导的导数值也相等,由倒数公式可得如式(14)所示：
b1+2c1x2=b2+2c2x2
b2+2c2x3=b3+2c3x3(14)
(4)设函数一的二阶导数值为0,可得如式(15)所示：a1=0(15)
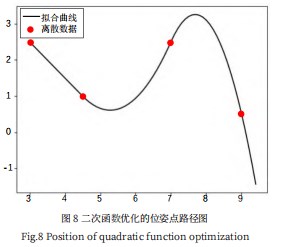
最后联立上面的九个方程组求出优化后的路径曲线,如图8所示。
2.2.2 teb_local_planner的参数调试
teb_local_planner[8]是TEB算法对应的参数文件,不同的参数值也会影响机器人对局部路径的规划,因此需要根据实际任务要求对参数进行调试。
(1)Robot param的调节,这一部分是对机器人行驶效果影响最大的参数。max vel_x和acc_lim_x是对线速度与线加速度的约束,机器人在避障时应慢慢减速,因此max vel_x和acc_lim_x都不应过大。max_ vel_theta和acc_lim_theta为角速度和角加速度,同理也不应过大。max vel_x_backwards为倒车速度,当机器人的转弯半径过大不容易避开障碍物时,机器人会向后倒车一段距离以保证避障效果,在上面对路径进行优化之后一般不会出现这种情况,所以使用default。min_turning_radius和wheelbase分别为机器人的最小转弯半径和车轮轴间距,这里根据我们机器人的实际情况进行设置。调试结果如下所示。
max vel_x:0.4
max vel_backwards:0.2
max vel_theta:0.3
acc_lim_theta:0.5
min_turning_radius:0.5
wheelbase:0.4
(2)Obstacles param的调节,这一部分是障碍物反馈信息的参数。min_obstacle_dist为机器人与障碍物之间最小的期望距离,根据上面计算约束值的需要进行设置。inftion_dist为设置缓冲区大小的参数,机器人在进入缓冲区范围内就开始减速,但不进行避障,这个参数过小会导致机器人有可能来不及避障导致避障失败,过大会导致机器人避障缓慢而且浪费时间。costmap_obstacles_behind_robot_dist为机器人测得距离后方的障碍物之间的间隔,因为后面的障碍物一般为已经避过的障碍物,如果再次进行计算不仅会浪费计算资源而且也不会对路径产生实质的优化效果,所以设为default。调试的结果如下所示。
min_obstacle_dist:0.27
inftion_dist:0.6
costmap_obstacles_behind_robot_dis:1.0
3算法仿真测试
3.1仿真模型建立
最后通过ROS平台对算法进行仿真测试,采用ROS平台提供的URDF建立机器人模型。URDF文件主要由以下四个标签组成：
(1)<joint>：描述机器人关节运动方向和速度限制的运动学和动力学属性。
(1)<link>：机器人的机械结构和物理属性,其中包括尺寸、颜色、惯性常量、碰撞系数等。
(3)<robot>：完整的机器人最顶层的标签,其他标签要在此标签下插入。
(4)<gazebo>：机器人模型在Gazebo仿真中需要的参数,包括机器人的材料属性、Gazebo插件等。
通过调用上述标签建立机器人模型,首先创建一个car ws的工作空间,然后在car_ws下创建URDF文件夹、meshes文件夹、launch文件夹和config文件夹。其中,将URDF或xacro文件放入URDF存文件夹,将URDF中引用的模型渲染文件放入meshes文件夹,将相关的启动文件放入launch文件夹,将RVIZ配置文件放入config文件夹。在URDF文件夹下创建car.urdf文件,并使用诸如“robot”、“link”之类的标签来构建无人驾驶模型。本设计模型包含了10个link,9个joint。9个joint分别负责这些link的连接方式。
由于整个URDF文件过于冗长,可以使用xacro简
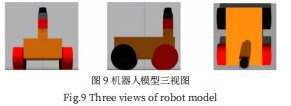
化模型文件,例如：使用常量定义常用变量,调用数学公式计算半径,使用宏定义重复使用模块,引用其他xacro文件。使用xacro精简化之后,添加标签,并编写launch文件,可以在Gazebo中查看机器人的真实外观,并且可以通过键盘来控制车辆移动。如图9所示为搭建的整车模型的三视图,至此,机器人模型的搭建完毕。
Gazebo可以为测试机器人建立一个模拟场景。加入模型库,里面有桌子,墙,锥桶,甚至人偶模型,以模拟真实世界。本设计使用Gazebo的Building Editor来构建出2D的赛道环境设计草图,通过给草图上的建筑物赋予相应的参数,例如长、宽和高,Gazebo中会生成对应的3D环境信息,至此,机器人的仿真世界物理环境设计完成。
3.2优化前后算法仿真对比
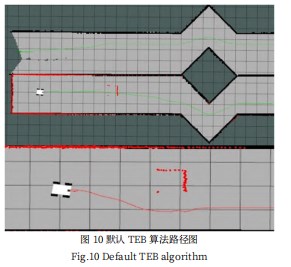
最后把建立好的四轮差速机器人运动学模型和优化的TEB算法通过ROS平台提供的RVIZ可视化界面[9,10]进行仿真测试。如图10所示中红色为改进前的TEB算法的局部路径,可以看出最大的缺点是避障时的路径不够圆润,而且局部路径选取的位姿点过多,导致局部路径规划的路径过长,浪费运算资源,增加了不确定性,不符合机器人运动的状态。
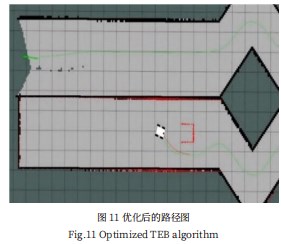
下面使用改进后的TEB算法进行仿真测试,路径图如图11所示。可以看出优化后的路径不管是全局还是局部都具有较好的圆滑度,而且局部路径的计算长度不是很长,既节省了运算资源也能够完美的避开障碍物。
4结论
本文通过四轮差速机器人,提出了一种优化的TEB算法,并做出仿真实验,结论如下。
(1)在建立四轮差速机器人简化模型的基础上,对TEB算法规划的局部路径使用二次样条插值法进行拟合优化,从而使局部路径更加圆滑,符合机器人的运动状态。
(2)将优化算法和机器人模型导入ROS平台,在RVIZ可视化仿真平台上进行仿真测试,通过仿真验证了优化的有效性,此后可将优化后的算法移植应用于工业生产领域的机器人,以提高其工作的稳定性。
参考文献
[1]郑凯林,韩宝玲,王新达.基于改进TEB算法的阿克曼机器人运动规划系统[J].科学技术与工程,2020,10(20):3997-4003.
[2]代婉玉,张丽娟,吴佳峰,等.改进TEB算法的局部路径规划算法研究[J].计算机工程与应用,2022,58(8):283-288.
[3]丁皓,刘浩宇,庄逸,等.基于四轮差速模型的多机器人路径规划[J/OL].控制工程:1-8[2022-06-10].
[4]GOEBEL R P.ROS by Example[M].California Willow Garage,2013,4:5-7.
[5]Lentin Joseph,Jonathan Cacace.Mastering ROS for Robotics Programming-2D[M].Packt Publishing Ltd,2018,2:321-358.
[6]毛志伟,吴训,周少玲,等.四轮驱动全轮差速转向移动焊接机器人运动学分析与仿真[J].中国机械工程,2016,7(6):1731-1734.
[7]李承远.基于改进TEB算法的自主导航控制[D].杭州:杭州电子科技大学,2020.
[8]朗坦•约瑟夫,乔纳森•卡卡切.精通ROS机器人编程[M].北京:机械工业出版社,2019,2:113-144.
[9]菜自兴.机器人学基础[M].北京:机械工业出版社,2020,12:150-166.
[10]余伶俐,周开军,陈白帆.智能驾驶技术路径规划与导航控制[M].北京:机械工业出版社,2020,5:40-61.
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！
文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jisuanjilunwen/42273.html
