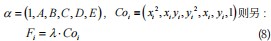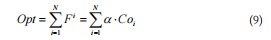SCI论文(www.lunwensci.com):
摘要:为了满足对椭圆目标抓取的需要,针对椭圆检测过程中,由于边缘信息的遮挡、断层、嵌套和背景复杂等原因,提出一种快速、抗干扰的椭圆检测算法。首先将彩色图像转变为灰度图像,经过边缘提取和细化算法得到细边缘信息图。利用8连通算子提取边缘图中的连续弧线段,并根据跟踪弧段左端点与弧中点连线的斜率变化,将弧段分为4类并确定拐点。对4种不同凹凸性和方向性的弧进行初始聚类,具体需要根据弧间线段中点连线与其他平行弧间线段中点位置关系和阈值比较,确定椭圆。应用几何最小二乘法拟合椭圆参数。
关键词:椭圆检测;椭圆拟合;边缘检测;梯度检测;最小二乘法
Ellipse Detection Algorithm Based on Midpoint Threshold of Parallel Chord
ZHANG Xiaoyuan,LIU Tangyou,YU Futing
(College of Information Science and Technology,Donghua University,Shanghai 201620)
【Abstract】:In order to meet the needs of capturing ellipse target,a fast and anti-interference ellipse detection algorithm is proposed for the reasons of occlusion of edge information,fault,nesting and complex background in the process of ellipse detection.Firstly,the color image is transformed into gray image,and the fine edge information image is obtained by edge extraction and thinning algorithm.The 8-connected operator is used to extract the continuous arc segments in the edge graph.According to the slope change of the line between the left end point and the middle point of the arc segment,the arc segment is divided into four categories and the inflection point is determined.For the initial clustering of four kinds of arcs with different concavity,concavity and directivity,it is necessary to determine the ellipse according to the comparison of the position relationship and threshold between the midpoint of the line between arcs and other parallel lines between arcs.Geometric least square method is used tofit ellipse parameters.
【Key words】:ellipse detection;ellipsefitting;edge detection;gradient detection;least square method
0引言
椭圆检测是机器视觉处理领域内的一项经典的目标检测问题。它在工业零件检测,交通信号路牌分类和生物天文图像识别中都具有广泛的应用。因此,数字影响中椭圆信息的提取应满足高效准确的要求。传统的椭圆算法可以大致分为两类:基于Hough变换及其衍生改进椭圆检测算法和基于弧段聚类边缘信息的椭圆检测算法。传统的Hough变换算法具有方法简洁和能够有效抑制噪声和交叉边缘等优点,文献[3]针对一维参数空间霍夫变换椭圆检测算法不能检测长轴端点缺损的椭圆这一缺陷,提出了两种改进算法。两种改进算法都是先确定椭圆中心,采用分步计算参数的方法,以降低霍夫变换参数空间的维数,从而降低算法整体的时间复杂度。文献[4]提出了一种有效的基于随机Hough变换的椭圆检测算法(RED),但是此类方法的时间复杂度和空间复杂度过高,需要在五维优化空间内进行投票择优拟合。对设备硬件算力要求高,计算时间久,故不适用于需要快速高效检测椭圆的场景。
考虑到实际工程实施中,待检测影响的边缘图信息常常有掩盖、截断等情况发生,完整的椭圆边缘会被分为一些相互孤立的弧段。无论是Hough变换还是最小二乘法的椭圆拟合检测算法,其处理的对象都是离散的采样点。针对有大片信息丢失的椭圆边缘,上述两类算法已不能胜任有效的椭圆检测目标。椭圆最主要的一个信息是边缘的连续弧和其椭圆的几何特性,因而比离散采样的边缘像素更具有代表性,故可以从椭圆弧边缘的代数和几何信息出发,跟随边缘信息进行椭圆检测。
最近几年,基于弧段及其衍生椭圆检测算法在实际丰富的数字影像识别检测中已经取得了一些成果。文献[5]针对对检测精度不高、占用空间大、运行时间长,提出了一种基于曲线跟踪的椭圆检测算法,通过检测轮廓线得到参数,判断是否为椭圆。文献[6]针对多个椭圆因重叠、遮挡、嵌套情况而存在检测效率与精度较低的问题,提出一种基于边界聚类的椭圆快速检测改进方法,以上在复杂图像中基于边缘跟踪的椭圆检测算法已经取得了良好的效果。文献[8]提出基于梯度分类与多边形辨识的椭圆快速检测方法。该方法通过边缘检测算子对采集的图像进行预处理,获取图像边缘的梯度信息,根据边缘灰度梯度与凹凸性将边缘线分为4类圆弧特征,通过对4类圆弧特征的聚类初步确定备选的椭圆集合,但是其对椭圆边缘弧段的提取都十分冗长,对边缘梯度信息的计算量过大,得到的候选椭圆弧段过多,无效的椭圆弧段占用过多的计算资源,容易产生虚假椭圆。
本文基于椭圆边缘弧段相关几何性质和代数性质,提出了一种新的椭圆检测过程,来解决其在弧段分类产生中和后续弧段聚类中的繁琐性。
1图像预处理
边缘信息的有效提取是椭圆检测算法的实施前提,边缘提取算法应该能够极大响应弧线段边缘并降低对背景及噪声信息的关注度。
椭圆信息的检测是基于像素值变化进行研究,对于彩色原图来说,三通道的数据量过于冗余,故需要将彩色图进行灰度变换。并通过灰度变换将目标物的灰度信息有效区别于背景信息。
传统的Canny算子针对水平和竖直两个方向的灰度梯度信息进行边缘提取,而椭圆的几何特性使得椭圆边缘大多数梯度方向并非水平和垂直。故可以采用改进的Sobel算子,提高对斜向边缘的优先响应。
若水平方向和竖直方向的梯度模板分别为Gx和Gy,则45°和135°方向的梯度模板表达式为:
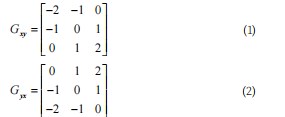
在增加了两个维度方向的梯度信息之后,每一个像素点会与周围3×3领域内像素点像素值形成的矩阵进行卷积计算得出Gx、Gy、Gxy、Gyx四个方向上的梯度分量,由此可以得知该像素点此时的梯度信息分量为:
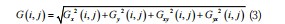
在结构信息复杂的数字图像中,图像边缘的灰度量级不一致。单一阈值的算子检测容易忽略灰度值梯度的变化,故采用自适应阈值的Canny算子进行灰度梯度变化与阈值的比较,更多提取完整的椭圆边缘信息。
椭圆检测的效率会受到待检测椭圆边界周围非椭圆无效边界影响,使得检测效率大大降低。本文通过细化边缘来提高椭圆边界在边缘特征图中的关注度,使得边缘图细化到单一像素的宽度,避免由于像素冗余致使不明显的边缘信息。
2弧段分类
弧段需要进行边缘信息进行分类处理,区别并剔除非弧段边缘。所以需要对边缘图中的边缘进行筛选和识别弧段边缘,采用8-邻接算子L对连续边缘段进行追踪。设边缘图的边缘灰度值为1,非边缘背景信息灰度值为0。8-邻接算子的定义为中心为0,上下左右、左上右上、左下右下为1。如图1所示:
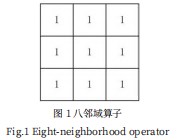
该算子遵循从上至下,从左至右的方式与细化边缘图进行卷积加权求和操作,规定图像的某9像素区域,其中g为其灰度值:
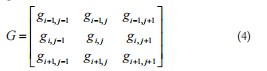
则8-邻接算子W与L其卷积的结果计为
当9像素区域均为背景信息时,W的值为0,当其中心是边缘段的端点时,W值为1,当其为边缘段的中间点时,W≥2。因边缘图为细化为1像素的边缘,故W=2。将卷积值W=1处的点记作一段边缘的一端点,并以有效值出现的方向为滑块前进方向,将算子中心置于新有效值出现位置,并将之前的有效边缘像素置0,以免像素值的重复计算。边缘段的获取过程如图2所示:
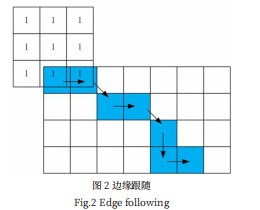
设置阈值thseg,统计各个边缘段的长度,当其有效长度小于给定阈值时可以认定其为噪点或非参考性的过段边缘端。
由椭圆的几何形状可知,一个完整的椭圆由4类弧段组成,这些弧段在椭圆中的分布位置如图3a1-a4所示:
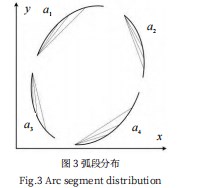
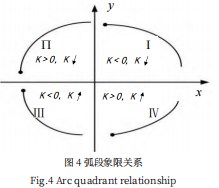
设椭圆弧段上的点为P(x,y,k),其中x,y为弧段边缘点在图像中的横纵坐标,k为该点与弧段左端点P1之间连线段的斜率。由椭圆的几何性质可知,椭圆弧段现有凹凸两个类别,当为凹弧段时,k值增大变化;当为凸弧段时,k值减小变化。故在使用8-邻接算子进行边缘识别时,根据边缘段长度大小设定采样点,并依次计算每个采样点与左端连线斜率变化方向。依据上述k值变化方向判定边缘弧段的凹凸性。椭圆段的凹凸性仅能代表Ⅰ、Ⅱ两种不同的弧段特性,于是引入弧段的方向性。若弧段若检测到算子前进梯度方向为右与右上时,即k>0则规定弧段方向为向上,若检测到算子前进方向为右和右下,即k<0则规定弧段方向为向下。于是按照分类方法,弧段被分成Ⅰ、Ⅱ、Ⅲ、Ⅳ4类,分别为下凸、上凸、下凹、上凹。每一类对应于笛卡尔坐标系的四个象限,如图4所示:
当在一段连续的边缘段上,点(x,y)与左端点P(xl,yl)连线斜率在四个象限分别满足下列变化图像,如图5所示:
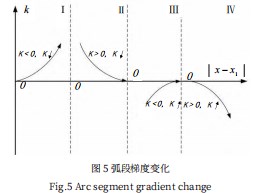
若边缘段过长,可以在一个边缘段中囊括2种以上的弧段种类,在单一边缘端中每类弧段的分界点是k符号或者变化方向跳变处。于是记录这些跳变点,以该点为分界点将边缘端分割,是每一个边缘端仅具有单弧段性质。设置阈值tharg,当截断后的弧段小于阈值时,则判定该段为过小弧段与噪声段,仅保留大于该阈值的弧段。
3椭圆候选集聚类
属于同一椭圆的不同弧段应该聚类于同一椭圆。由于复杂影响目标造成的边缘丢失遮盖,规定一个椭圆由3类不同的弧段组成,则一个椭圆可以一共有4种不同的弧段组合,记不同的组合为C。
设在边缘图中某一类弧的数量为Q,则可能的组合数量为O(Q3)。庞大的数据量显然不能直接选取弧段组,故需要依据筛选标准和条件进行弧段组合。
本文对弧段分组的约束条件有两个,首先同一椭圆的不同弧段应满足笛卡尔坐标系中的象限对应关系,其次利用两辆弧段平行线中点几何关系交叉验证,排除不满足要求的弧段组。
第一个约束条件确保了每三个一组弧段由来自三个不同对应象限。
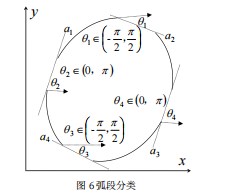
如图6所示,从图中圆弧的几何关系可以看出,相邻两个象限的弧段端点之间连线的斜率信息应满足以下几个条件:
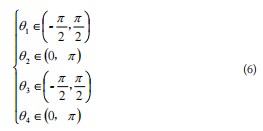
式中:规定从左至右为水平正方向,角度θ表示两相邻象限弧段之间的连线与正方向形成的夹角。当两相邻弧段不满足上述参数不满足上述约束关系,不能归为同一弧段组。通过上述条件筛选,可以排除一系列不符合要求的弧段。
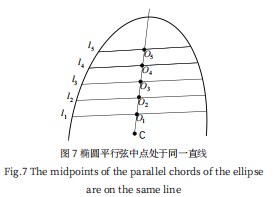
第二个约束条件是为了确定两个相邻象限弧段属于同一椭圆。根据椭圆几何性质可知,椭圆的一组平行弦的中点处在同一条直线上,并且过该椭圆的椭圆中心。如图7所示:
设定阈值
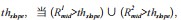
可
见两相邻弧的两组任一组平行弦中点不具备一个椭圆的几何性质,故可以将这对弧组排除。
经过两次弧组约束条件的筛选,可以排除一大部分无效的弧组,使得候选参数空间占用减少。
4椭圆拟合
在二维坐标系中,椭圆一般可以用以下的圆锥曲线隐式表示:
x2+Axy+By2+Cx+Dy+E=0(7)
将上式左端分解为两个向量的乘积,用α代表椭圆
隐式表达式参数向量,Coi表示候选弧段的采样点坐标
为了求出5个未知数,需要在一组弧段内的采样点至少为5组,由于一组弧段为3个,故根据弧段长度自适应间断采样,获得坐标向量组。
因为图像的边缘点采样点与理想椭圆参数存在误差,故上式不为零,不能求出唯一解,但可以通过最小二乘法拟合求出最小近似解。将圆锥曲线的求解问题转化为求解误差方程最小值的问题:
N为采样点数目,根据极值定理,其求解条件为:
由此可以得到6个线性方程,于是可以求出其参数解。
以下是用本文方法对图片进行处理的结果图,如图9所示:
 新算法与随机霍夫变换的比较结果,如表 1 所示 :
新算法与随机霍夫变换的比较结果,如表 1 所示 :
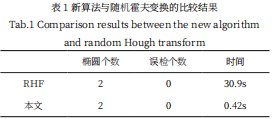
两种算法都检测出了指定的椭圆个数,但其在时间消耗上差距巨大,随机霍夫变换因其庞大的参数空间导致运算缓慢,而本文基于弧段阈值算法能够根据边缘图像快速进行有效边缘筛选,计算参数大大减少,能够满足实时性的要求。
5结论
(1)传统Hough变换及其改进的椭圆检测算法需要对每个前景点进行累加,计算量大,新算法剔除了明显不属于椭圆的曲线,减少计算量,满足在线检测对实时性的要求。
(2)对于有遮挡缺失的椭圆,本算法不要求椭圆边缘完整,只需有椭圆的部分边缘就可以识别,而传统RHF算法需要比较完整的椭圆才可以进行拟合。
参考文献
[1]成浩,崔文超.基于Hough变换的椭圆检测算法对比分析[J].软件导刊,2018,17(0 9):115-118+121.
[2]陈余根,杨艳.基于霍夫变换椭圆检测的两种改进算法[J].半导体光电,2017,38(05):745-750.
[3]霍天欢,陈临强.基于一维Hough变换的椭圆检测改进算法[J].杭州电子科技大学学报,2011,31(02):54-57.
[4]李良福,冯祖仁,贺凯良.一种基于随机Hough变换的椭圆检测算法研究[J].模式识别与人工智能,2005,18(04):459-464.
[5]李振坤,闫志华,王占云.一种基于曲线跟踪的快速椭圆检测算法[J].机械设计与制造,2018(10):245-248.
[6]吴尧锋,王文,卢科青,等.边界聚类椭圆快速检测方法[J].浙江大学学报(工学版),2016,50(03):405-411.
[7]刘志慧,夏勇.基于曲线弧分割的椭圆检测方法[J].计算机技术与发展,2015,25(10):19-23+28.
[8]吴晨睿,张树有,何再兴.基于梯度分类的复杂背景椭圆快速检测方法[J].浙江大学学报(工学版),2018,52(05):943-950.
[9]王春芳,高煜妤.一种新的基于弧段提取的椭圆检测方法[J].计算机测量与控制,2015,23(02):587-589+592.
[10]闫蓓,王斌,李媛.基于最小二乘法的椭圆拟合改进算法[J].北京航空航天大学学报,2008(03):295-298.
[11]陈若珠,孙岳.基于最小二乘法的椭圆拟合改进算法研究[J].工业仪表与自动化装置,2017(02):35-38+46.
[12]全燕鸣,凌泉.基于几何对称性的椭圆拟合算法[J].自动化与仪表,2020,35(05):51-55.
[13]徐则中,游庆祥,钱诚.椭圆对象参数的快速提取[J].江苏海洋大学学报(自然科学版),2020,29(04):1-7.
[14]WANG Yong-tao,HE Zhe-qi,LIU Xi-cheng,et al.A Fast and Robust Ellipse Detector Based on Top-down Least-square Fitting[C]//British Machine Vision Conference 2015.
[15]Kwon B K,Kang D J.Ellipse detection method based on the advanced three point algorithm.IEEE,2015:1-5.
[16]DONG H X,PRASAD D K,CHEN I M.Accurate Detection of Ellipses with False Detection Control at Video Rates Using a Gradient Analysis[J].Pattern Recognition,2018,81:112-130.
[17]Claudia Arellano,Rozenn Dahyot.Robust Ellipse Detection withGaussianmixturemodels[J].PatternRecognition,2016:12-26.
[18]Viorica Pătrăucean,Pierre Gurdjos,Rafael Grompone von Gioi.Joint A Contrario Ellipse and Line Detection[J].IEEE Transactions on Pattern Analysis and Machine Intelli gence,2017,39(4):788-802.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/42223.html
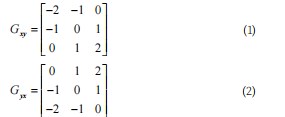
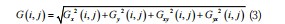

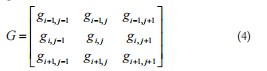
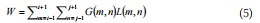




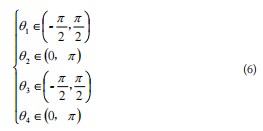
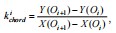 ,前后两个线段斜率相减的范数之和表达该组中点的位置相关性,
,前后两个线段斜率相减的范数之和表达该组中点的位置相关性, 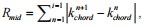 对每一对相邻象限弧组,取两组平行弦,取远端端点引一条线段值另一弧中一点a,记该线段为基弦,并以相同斜率求取一组平行弦。如此一来一对相邻象限弧组就有一对平行弦组。其中点相关性记作R,R,如图8所示:
对每一对相邻象限弧组,取两组平行弦,取远端端点引一条线段值另一弧中一点a,记该线段为基弦,并以相同斜率求取一组平行弦。如此一来一对相邻象限弧组就有一对平行弦组。其中点相关性记作R,R,如图8所示: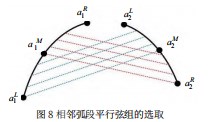
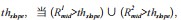 可见两相邻弧的两组任一组平行弦中点不具备一个椭圆的几何性质,故可以将这对弧组排除。
可见两相邻弧的两组任一组平行弦中点不具备一个椭圆的几何性质,故可以将这对弧组排除。