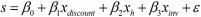SCI论文(www.lunwensci.com):
摘要:本文选取了产品的销售量、价格折扣、节假日和库存量等特征,建立了零售产品的需求预测模型:回归模型和神经网络模型。这两种模型预测值的MAPE有一定的可靠性,模型可以用来对零售产品的需求进行预测。
关键词:线性回归模型;神经网络模型;MAPE
Neural Network Model for Demand Forecasting of New Retail Products
WU Yuheng,WU Changjian,LI Yu,HUANG Danyang
(Zhujiang College of South China Agricultural University,Guangzhou Guangdong 510900)
【Abstract】:This paper selects the characteristics of product sales volume,price discount,holidays and inventory,and establishes the demand prediction model of retail products:regression model and neural network model.The MAPE of the predicted values of the two models has a certain reliability and the two models can be used to predict the demand of retail products.
【Key words】:linear regression model;neural network model;MAPE
受到互联网的影响,我国消费市场也在不断的发生变化。市场上的消费模式已经逐步由“以客为主”代替“以物为主”。在新零售行业,性价比不再是顾客衡量是否购买物品的唯一标准,而是把注意力放在“个性化、时尚、美观”等方面。在消费者需求的推动下,新零售企业的生产模式逐步向多品种、小批量前进。这样让零售店铺里的商品种类更加琳琅满目,同时也给零售行业的库存管理增加了很大的难度。如何能对新零售产品给出精准预测,是当前大多数新零售企业需要重点关注并思考的问题[1-5]。
1数据来源
本文数据来源为赛氪官网赛题(https://www.saikr.com/c/nd/6456)。根据相关问题对数据的需求和原数据的特点,首先读取附件数据表,筛选出累加销售额前50的skc(单款单色),有效数据共24601条,接着利用筛选出的数据建立回归模型和神经网络模型,用于预测skc销售量。
2线性回归模型
建立如下的线性回归模型:
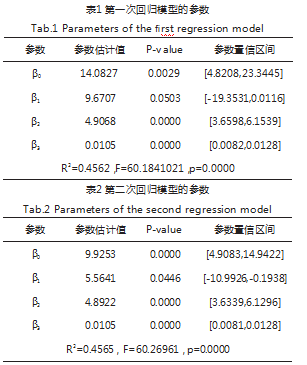
其中s表示销售量,xdiscount表示商品价格的折扣,xh表示节假日虚拟变量,xinv表示库存量。如果当天是节假日,则xh=1,否则xh=0。利用MATLAB求解,得到模型的回归系数估计值及其置信区间(置信水平α=0.05)、检验统计量R2、F、p的结果见表1。
表1显示,R2=0.4562指因变量s(销售量)的45.6%可由模型决定,F值远远超过F检验的临界值,p远小于α,因而模型从总体来看是可用的。不过回归系数β1的置信区间包含零点,表明回归变量xdiscount是不太显著的。由于xdiscount是表示商品售价的折扣,从回归结果来看,在置信水平α=0.05下,商品售价的折扣对销售量影响不显著。在实际销售中,折扣还是会对人们的购买欲望有影响的,但不是线性影响。因此,调整回归模型,将回归变量xdiscount换成x2discount,即折扣的平方。重新求解模型,结果见表2。
表2显示,R2=0.4565指因变量s(销售量)的45.65%可由模型决定,F值远远超过F检验的临界值,p远小于α。在置信水平α=0.05下,三个变量对s(销售量)的影响是显著的,因而模型是可用来预测商品的销售量,具体回归模型如下:
系数β1=-5.5641表明商品降价10%平均每天能增加1单位的销售量,β2=-4.8922表明节假日平均每天能增加4.8922单位的销售量,这些说明了商品打折和节假日能促进消费。
3神经网络模型
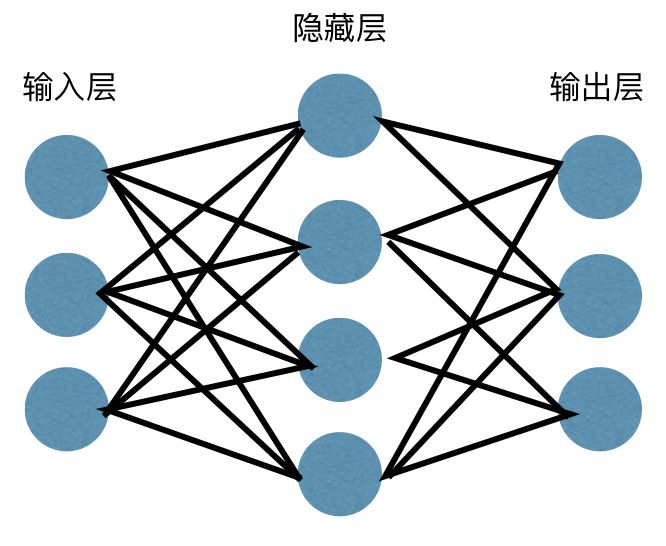
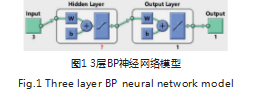
建立3层BP神经网络,训练数据算法采用Levenberg-Marquardt,输入数据为折扣、节假日虚拟变量以及库存量,输出变量为销售量。如图1所示。
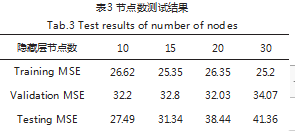
为了评价神经网络模型的性能和泛化能力,将数据随机分成训练样本(75%)、检验样本(15%)和测试样本(15%)。在BP神经网络中,隐藏层节点数的选择非常重要,为了选择合适的隐藏层节点数,可以考虑取不同的节点数进行测试。隐藏层的节点数依次选10、15、20、30,各训练10次神经网络,并计算训练样本均方误差的平均值、检验样本均方误差的平均值和测试样本均方误差的平均值,如下表3所示。
上表显示,随着隐藏层的节点数由10增加到30,测试样本均方误差的平均值由27.49一直增加到41.36,因此隐藏层的节点数选为10比较合适。
4两种模型的比较
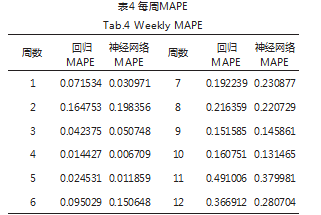
利用建立好的回归模型(2)和神经网络模型预测目标skc在2019年10月1日后12周内每周的周销售量,并计算每周预测值的平均绝对百分比误差MAPE。如表4所示。
表4显示,神经网络模型预测值的MAPE和回归模型预测值的MAPE差别不是很大。两种模型前10周预测值的MAPE在0.25内,预测效果基本上可以认为较可靠。不过两种模型11周和12周预测值的MAPE就很大了,这也说明了模型不够稳健。
5结语
本文建立了回归模型和神经网络模型,这两种模型的预测有一定的可靠性,可以用来对零售产品的需求进行预测。不过这两种模型预测值的MAPE有时会很大,这表明了模型不够稳健,仍需要进一步探索,寻找精度更高、稳健度更好的模型。
参考文献
[1]何无霜.消费者网络购物影响因素探究[D].南京:南京大学,2017.
[2]李洋,张朋朋.新零售的发展及其对居民消费的影响[J].电子商务,2020(5):61-63.
[3]王雨帆.线上线下一体化视角下传统零售企业消费者粘性影响因素分析[J].商业经济研究,2020(6):121-124.
[4]余昕杰.“新零售”商业模式对零售业企业的影响研究[J].中国市场,2020(6):125-126.
[5]苑卫卫.新零售视角下消费者体验影响要素分析[J].商业经济究,2020(4):78-80.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/37379.html