SCI论文(www.lunwensci.com)
摘 要:本文探讨了神经网络模型在系统响应预测中应用的可能性。首先介绍了人工智能概念,主要包括决策树、深度学 习、神经网络等主要人工智能算法的优势及特点。然后,针对不同的系统响应预测案例,建立了神经网络模型,并对不同系统 响应的预测性能进行了比较。最后,分析了基于神经网络模型的系统响应预测的可行性。
关键词:系统响应预测,人工智能.神经网络
Research on the Application of Neural Network Model in System Response Prediction
DU Bairun1. LI Shuang2. ZHONG Xiaoying2
(1.Dalian University of Technology School of Economics and Management, Dalian Liaoning 116024;
2.China Ship Development and Design Center Science and Technology on Electromagnetic Compatibility Laboratory,
Wuhan Hubei 430064)
【Abstract】: This paper explores the possibility of using neural network models in system response prediction. Firstly, the concept of artificial intelligent, including the principles, characteristics, and advantages of major algorithms such as decision trees, deep learning, and neural network are introduced. Then, several system response estimation examples are conducted and a NN-model is established, the estimation performance is analyzed through simulation. Finally, the feasibility analysis of NN-model based system response estimation is performed.
【Key words】: system response estimation;artificial intelligent;neural network
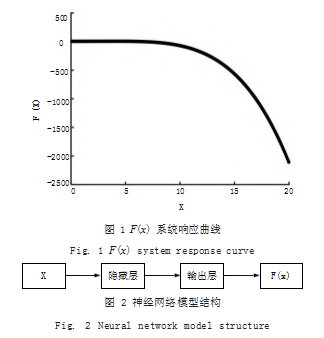
0 引言:系统的定义为若干部分相互联系、相互作用, 形成 的具有某些功能的整体。系统有一定的功能,或者说系 统具有一定的目的性,系统的功能是指系统与外部环境 相互联系和相互作用中表现出来的性质、能力和功能。 我们在评估一个系统性能时,最关注外部因素输入系统 后,经过系统响应所造成的影响,这就需要建立一个系 统模型,通过系统模型的建立,结合外部因素输入,就 能获得对系统模型所表征对象的输出影响的预测。一般 地,系统响应分为线性响应和非线性响应,线性响应的 系统建立系统响应模型较为容易,而我们所研究的对象 往往比较复杂,单纯的线性响应,甚至是数学理论公式 都难以表征。
人工智能(Artificial Intelligent,AI) 是研究开 发能够模拟、延伸和扩展人类智能的理论、方法、技术及应用系统的一门新的技术科学,得到了愈加广泛的重 视,并在经济政治决策、控制系统、仿真系统中得到应 用,其通过学习的方法,从解决一类问题的经验中获取 知识、学习策略,在遇到类似的问题时,运用经验知识 解决问题并积累新的经验,在复杂系统响应预测方面, 如电子电路系统设计 [1]、能源消耗预测 [2]、经济学规律 预测 [3] 等,具有广泛的应用前景。
本文将首先介绍人工智能概念,主要包括决策树、 深度学习、神经网络等主要人工智能算法的优势及特 点 ;然后,探讨神经网络模型在系统响应预测中应用的 可能性,针对典型系统响应预测案例,建立神经网络模 型,并对预测性能进行比较分析 ;最后评估了神经网络 模型在不同系统响应预测中应用的可行性。
1 人工智能算法特点及分析
根据学习经验(知识) 可将人工智能算法分为 :监督学习算法、无监督学习算法、半监督学习算法 [4]。
1.1 监督学习算法
常用算法有很多,包括线性分析法(LinearAnalysis)、 朴素贝叶斯法(Naive Bayes)、决策树(Decision Tree)、 支持向量机(Support Vector Machine,SVM)、神经网 络(Neutral Network, NN)、集成学习(Ensemble Learning)等,此处仅介绍使用较多的方法。
(1) 线性分析法 :来源于统计学,其中最小二乘法 是使用最广泛的回归学习算法之一。通过对优化目标调 整、改进衍生出 Ridge Regression、Lasso Regression 等算法。(2)朴素贝叶斯法 :基于概率论的分类方法。 在贝叶斯理论中,该方法要求所有特征之间相互独立。 (3)决策树 :源自风险管理的辅助决策系统,是一个利 用树状模型的决策支持工具,根据其建分支的策略不同 派生了很多子算法, 如 ID3、C4.5、CART 等。其优点 是学习结果易于人类理解 ;缺点是当数据集变化时,决 策图变化较大。(4)支持向量机 :20 世纪 60 年代被提 出, 直到 1992 年由 Bernhard E. Boser 等人改进为可 以应用于非线性问题后被广泛应用,在 21 世纪初期的 很长时间里被认为是最好的分类器。(5)神经网络 :源 于生物神经学,具有较长历史,可以处理复杂的非线性 问题。研究一度停滞,随着计算机计算能力的提升和卷 积网络结构的提出,发展出深度学习,已经成为当前非 常强大的工具。(6)集成学习 :一种利用若干个基础分 类器共同执行决策的方法。近来被广泛应用,随机森林 正在逐步取代 SVM 的地位。此外,还有以 Adaboost 为代表的提升方法。
1.2 无监督学习算法
主要包括聚类和降维两类。聚类算法,根据不同的 策略模式,如距离切分、密度划分等,可划分为不同的 方法。
(1) 距离切分方法(Partition Method) :根据特 征之间的距离进行聚类划分,是一种最基础的算法,主 要是指 K- means 及其派生算法。(2)密度划分方法 (Density Method) :通过定义每个子集的最小成员数 量和成员之间距离实现划分。最典型的算法是 Density- Based Spatial Clustering of Applications with Noise,DBSCAN。(3) 模型方法(Model Method) : 以概率模型(以高斯混合模型为典型,即 Gaussian Mixture Model) 和神经 网络模型(Self-Organizing Map, SOM)为主要代表。其特点是不完全将样本认 定为属于某子集,而是指出样本属于各子集的可能性的 大小。(4) 层次方法(Hierarchical Method) :将数据集划分成有父子关系的树形结构。同时考察各子类之 间的亲缘关系, 比较典型的是 BIRCH(Balanced Its Reducing and Clustering using Hierarchies)模型。
而对于降维算法,则一般被用来压缩特征数量以便 后续处理。主要有 :线性降维,用于处理线性问题。模 型比较简单,具体包括主成分(Principle Component Analysis,PCA) 和线性判别分析(Linear Discriminate Analysis,LDA)。流行学习(Manifold Learning) :可 处理非线性降维, 目前比较成熟的算法包括 Isomap、局 部线性嵌入(Locally Linear Embedding,LLE)等。
1.3 强化学习
强化学习倾向于在动态环境中寻找合理的行为决 策,相对独特的分支。其行为主体是一个在某种环境中 独立运行的 Agent,通过训练获得在该环境中的最佳行 为模式,包含以下几个要素 :
(1)智能体(Agent) :是可采取一系列行动以达 到某种目标的控制器,如自动驾驶的控制器 ;(2)环境 (Environment) :是智能体所能感知和控制的世界模 型。如自动驾驶环境是智能体能感知到的路况和车本身 的行驶能力 ;(3)状态(State) :是任意静态时刻智能 体能感知到的环境情况 ;(4)行为(Action) :是智能体 能在环境中执行的行为 ;(5)反馈(Reward) ;是智能体 执行某个 / 某些行为后获得的结果,包括正、负反馈。
2 基于神经网络模型的系统响应预测
一个简单的神经网络的逻辑架构分成输入层、隐藏 层和输出层。输入层负责接收信号,隐藏层负责对数据 的分解与处理,最后的结果被整合到输出层。每层中的 一个圆代表一个处理单元,可以认为是模拟了一个神经 元,若干个处理单元组成了一个层,若干个层再组成了 一个网络,也就是“神经网络”。在神经网络中,每个 处理单元事实上就是一个逻辑回归模型,逻辑回归模型 接收上层的输入,把模型的预测结果作为输出传输到下 一个层次。通过这样的过程,神经网络可以完成非常复 杂的非线性分类,也就是具备对复杂的系统非线性问题 进行预测 [5-10]。
典型系统响应可以用多项式表示如式(1)所示 :
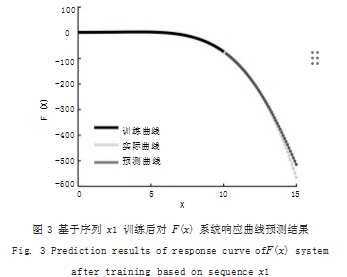
建立浅层神经网络模型,如图 2 所示,隐藏层神经 元数量设为 5.利用序列 x1 和对应的 F(x1) 对神经网络 模型进行训练,序列 x1 范围为 0.1 ~ 10.预测序列 x2对应的 F(x2), 序列 x2 范围为 10 ~ 15.如图 3 所示, 可以看到预测曲线与实际曲线存在一定差距,计算预测 曲线值与实际曲线值的相对误差均方根值为 0.0352.
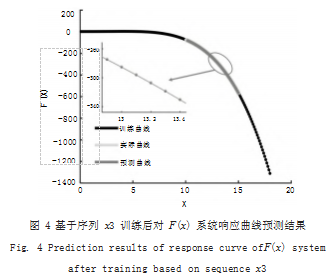
构造序列 x3 和对应的 F(x3) 对神经网络模型进行训 练,序列 x3 范围为 0.1 ~ 10. 以及 15 ~ 18. 预测序 列 x2 对应的 F(x2),如图 4 所示,可以看到预测曲线与 实际曲线基本吻合,计算预测曲线值与实际曲线值的相 对误差均方根值为 0.0027.相对于仅用 x2 序列进行训 练,获得的预测性能明显提升。
改变系统响应,表示如式(2)所示 :
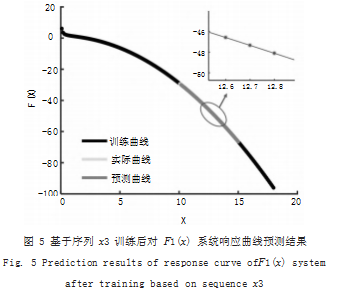
假设 a2=-0.3. a1=0.5. a0=1.采用上述构建的神经 网络模型和训练序列 x3 及对应的 F1(x3),则序列 x2 对 应的系统响应曲线 F1(x) 如图 5 所示,计算预测曲线值与实际曲线值的相对误差均方根值为 9.9e-6.可以看到 本文提出的基于神经网络模型能对不同的系统响应曲线 进行预测。
神经网络模型对任意系统响应进行建模和预测,包 括线性模型、多项式模型、记忆模型、无记忆模型等, 上述结果基于神经网络模型对系统非线性响应进行了建 模和预测,所预测对象在训练对象范围之外,神经网络 模型预测有一定的偏差,若所预测对象在训练对象范围 之内,神经网络模型预测性能较好,上述结果在系统响 应预测中对所采集的数据要求提供了指导,能够为复杂 系统响应预测提供较好手段。
3 结论
本文首先介绍了人工智能的概念,其中主要的人工智能算法,包括决策树、深度学习、强化学习等的原理 以及特点,并对各种算法进行了优势分析。然后,基于系统响应特点,重点研究了神经网络模型,运用浅层神 经网络模型对不同的系统响应曲线进行了预测,并与实 际系统响应曲线进行了比较,可以看到神经网络模型能 够在系统响应预测中发挥作用,为复杂系统响应预测提 供技术手段。
参考文献
[1] 许弘,刘军,李志强,等.基于神经网络的微波集成电路补偿模 型设计[J].杭州电子科技大学学报(自然科学版),2021.41(5):7- 13.
[2] 刘社民,李建功,裴付中,等.基于改进神经网络算法的电力系 统经济调度[J].吉林大学学报(信息科学版),2019.37(1):80-87.
[3] 冯娇,李红朴.基于优化小波神经网络的宏观经济预测技术 研究[J].现代电子技术,2019.42(7):181-183+186.
[4] 林树森.机器学习观止:核心原理与实践[M].北京:清华大学 出版社,2021.
[5] 南敬昌,赵景梅,袁杰.基于RBF神经网络的射频功放行为模型研究[J].计算机工程与应用,2011.47(8):125-127+134.
[6] 闫海鹏,吴玉厚,郭维城.基于神经网络的功率放大器预失真 建模[J].微电子学,2017.47(1):100-105.
[7] ESTARAN J,RIOS-MUELLER R,MESTRE M A,et al.Artificial Neural Networks for Linear and Non- Linear Impairment Mitigation in High-Baudrate IM/ DD Systems[C]//Ecoc,European Conference on Optical Communication.VDE, 2016.
[8] AHMAD S T,KUMAR K P.Radial Basis Function Neural Network Nonlinear Equalizer for 16-QAM Coherent Optical OFDM[J].IEEE Photonics Technology Letters,2016.28(22):2507-2510.
[9] 于欣平.基于神经网络的数据挖掘分类算法比较和思考[J]. 微型电脑应用,2018.34(7):94-96.
[10] 方芳.基于神经网络算法的大数据分析方法研究[J].软件工 程,2018.21(09):34-36.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/63307.html