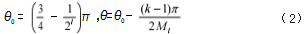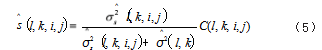SCI论文(www.lunwensci.com):
摘 要:本文研究了两种新的基于多尺度分析的阈值去噪方法,分别是基于 Curvelet 变换的局部 Winner 滤波去噪和基 于非下采样 Contourlet 变换的自适应阈值去噪,同时在估计子带系数方差的时候,设计了弧型窗口来完成,更符合 Curvelet 变换和 Contourlet 变换各向异性的特征,用文中方法进行图像去噪实验,提高 PSNR 值的同时,视觉效果也比较好,保留了 图像本身的一些细节特征。
关键词:Curvelet 变换 ;非下采样 Contourlet 变换(NSCT) ;子带自适应阈值 ;弧形窗 ;图像去噪
Research on Image Denoising Method Based on Multi-scale Analysis
CAO Fangju
(Hebei Vocational University of Technology and Engineering, Xingtai Hebei 054001)
【Abstract】: In this paper two new threshold denoising methods based on multi-scale analysis are studied, which are local Winner filter denoising based on Curvelet transform and adaptive threshold denoising based on non down sampling Contourlet transform, at the same time, arc windows are designed to estimate the variance of subband coefficients, which is more in line with the anisotropic characteristics of Curvelet transform and Contourlet transform, the image denoising experiment is carried out with the method in this paper, while improving the PSNR value, the visual effect is also better, and some detailed features of the image itself are retained.
【Key words】: Curvelet transform;nonsubsampled Contourlet transform(NSCT);adaptive threshold by subband; arc window;image denoising
0 引言
图像中的噪声对图像分析、图像压缩等高层图像处 理影响很大,所以图像恢复一直是图像处理中最重要的 一部分。利用小波变换去噪是曾经流行的方法,但是小 波变换方向性差,而实际的图像,其边缘往往具有多样 性,针对这一点小波变换有一定的局限性,去噪效果也 会受影响,所以多尺度分析流行开来,如 Curvelet 变换、 Contourlet 变换等,它们能够更好的表示二维图像, 最大程度的保留图像的细节、边缘等信息。再配上合适的图像去噪算法,就会得到比较好的去噪效果。
阈值去噪是最常用的去噪方法,选择合适的阈值往往 能够改善去噪效果,而阈值的选择与图形进行变换后的系 数方差及计算方差的窗口有很大关系,所以选择合适的图像表示方法以及适应其特性的窗口,理论上肯定会改善图 像去噪的效果,文献 [1] 提出非下采样小波变换域空间自适 应 Bayesian 缩减方法 , 它采用固定尺寸的方形窗口来估 计信号的方差,实际上,这类方形窗口是各向同性的,其 方向选择性差。Curvelet 变换和非下采样 Contourlet 变 换 [2] 具有很强的方向性,主要针对曲线奇异性的信号, 其各向异性特征非常有利于图像边缘的高效表示。曲线 特性是这两种图像变换表示方法优于小波变换的主要方 面,这就要求在估计信号方差时,所选择的窗口应该能体现这一特征,即要求窗口的方向应该与子带系数的能 量分布趋势相一致,因此,我们设计了一种弧形窗口。
1 弧形窗口定义
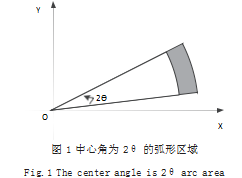
我们以当前待处理系数为中心,选取曲线特征明显的弧形区域,图 1 所示是中心角为 2θ 的弧形区域。其表达式为 :

其中,r 是弧形窗所对应大圆的半径,r 越大,窗 内包含的系数个数越多 ;θ 是弧形窗口对应中心角的一 半,通过调节 θ 的值,能够使弧形窗有更好的方向选择性,可以看出 :θ=90°时,该弧形窗就变为方形窗口, 所以弧形窗比方形窗更具有通用意义。
2 弧形窗口参数的选择
为使弧形窗口该弧形窗有更好的方向选择性,我们选择 θ 时,考虑当前子带的尺度信息和方向信息,使得在不同的子带内, θ 值也不同,从而弧形窗与子带系数的能量分布趋势相一致。这里,我们选取 :
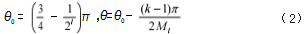
式中, Ml (l = 2,...L)为每一个分解尺度 l 上方向子带的个数,L 为分解的最大尺度数,k 表示当前方向子带。对于 r 的选取,我们采取多次实验,通过比较发现,r 取 2 时效果最好。
3 弧形窗局部 Wiener 滤波
假设原始图像被零均值、方差为 σ2 的加性高斯白噪声所污染,在 Curvelet 变换域,含噪图像可表示为 :

其中C(l, k, i, j )、s (l, k, i, j )和ε (l, k, i, j )分别是含噪图像、原始图像和噪声在第 l 层的第 k 个子带位置
(i,j) 处的 Curvelet 系数。
局部 Wiener 滤波的几个步骤中,有两个至关重要的步骤 :估计每一个子带上的噪声方差和当前系数的信号方差。对于 Curvelet 域子带内噪声方差 σ2(l,k) 的估计,目前还没有明确的解析形式。J-L.Starck[3] 等人给 出了利用 Monte-Carlo 技术的噪声方差估计方法,作 为一种近似的求解方案。基于这一技术的噪声方差估计 也被用在本文给出的去噪方法中。
在确定 σ
2(l,k) 后, σ
s2(l,k) 的估计是关键,不难发现,σ
s2(l,k)的值不仅随着尺度、方向的变化而变化,而且在同一个子带内,不同的空间位置(比如边缘与平坦区 域)的图像方差也相差很大,因此在同一子带内采用相同 的 σ
s2(j,l) 估计是不合理的,保证方差估计具有空间局部 适应性特点的方法是 Miback 提出的基于局部自适应窗口 的极大似然估计法,每一个位置处信号的方差 σ
s2(l,k,i,j) 由 C(l,k,i,j) 的邻域的 Curvelet 系数来估计 :

这里,(x)+=max{0,x},W, 和 #W 分别表示窗和窗的 大小,我们采用上面定义的弧形窗。这两个关键的问题 解决后,原始图像的每一个 Curvelet 系数可由下面的 Winner 滤波器公式估计得到 :
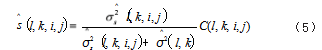
把弧形窗口用到信号方差估计式时,相应的算法我 们称之为弧形窗局部 Winner 滤波。把这种滤波算法应 用于图像去噪,得到了比较清晰的去噪结果。
4 子带自适应阈值去噪
文献 [4] 提出一种小波域和尺度相关的自适应阈值去噪 方法,但由于小波变换只有水平、垂直、对角线 3 个方向, 其方向选择性差,为此,我们选择非下采样 Contourlet 变 换来更好的表示图像细节特征,并且利用上面设计的弧 形窗定义了一个在各方向子带上自适应的阈值。
设 f 是受噪声污染的图像,模型为 :

其中,g 是原始图像, ε 是服从均值为 0,方差为 σn2 的高斯白噪声,即ε ~ N(0,σ) ,去噪的目的就是从观察 图像 f 中恢复原始图像 g。
对式(6) 进行非下采样 Contourlet 变换(NSCT),

y
t(i,j)、x
t(i,j)、n
t(i,j) 分别是噪声图像、原始图像、 噪声 在第 t 个细节方向子带的系数 ,t=1… N,N 表示所 有的细节方向子带个数。
自适应阈值稍加修改即可变为子带自适应阈值 :

s 是当前方向子带所在的层数,J 表示最大的尺度, σ
t 是用 Monte-Carlo 仿真估计的第 t 个细节方向子带 的噪声标准差, σ
tx (i,j) 是第 t 个细节方向子带点 (i,j) 的 信号标准差。
两个阈值参数x、σ
th 在非下采样 Contourlet 域即为 :

N1、N2 分别表示第 t 个细节方向子带纵、横方向的 系数个数。
具体的仿真实验步骤如 :
(1)对噪声图像应用 NSCT。
(2)用 Monte-Carlo 仿真估计第 t 个细节方向子带 的噪声标准差 σ
t。
(3)对于每一个细节方向子带内的系数,根据式
(1)选取弧形窗。估计每一点的信号方差 :

并用式(10)计算阈值参数 σ
tth,M 表示窗内系数 的个数。
(4)对于每一个细节子带,用式(9)计算阈值参数
−σ
tth,如果σ
tx t < σ
tth ,则用式(8)计算阈值,否则,阈
值为零。
(5)对于第 t 个细节方向子带内的每一个系数,以T(i,t) 为阈值,用软阈值函数进行处理,即 :

(6)把处理后的系数和未处理的低通部分一起进行 逆 NSCT,得到去噪图像。
5 实验结果及分析
我们选用 Lena 256×256 和 Peppers 256×256 图 像作为测试图像,对这两幅图像分别加入标准差为 10, 15,20 和 25 的零均值加性高斯白噪声,分别利用基于 Curvelet 变换的局部 Winner 滤波方法和基于 NSCT 的子带自适应阈值去噪方法,选取弧形窗口估计信号点 方差,根据多次试验结果表明,从粗分辨级到细分辨 r分别取 4,5,6,7 时效果最好。整个实验的性能评价 通过峰值信噪比 (PSNR) 来定量进行,单位为 dB,如 表 1 所示。
图 2(a) 为 噪声 图像, 对 比 图 2(b)、(c)、(e) 可以发现,用弧形窗局部 Winner 滤波去噪后 Lena 的 帽子边缘和纹理更清晰,整体视觉效果也较好 ;因为局 部 Wiener 滤波方法不会对系数造成“过扼杀”,而且 选用与 Curvelet 曲线特征对应的弧形窗口估计信号方 差,使 Curvelet 善于表示图像边缘的优势得到更好的 发挥 ;至于本文中第二种去噪方法,由于我们所选取的 阈值具有子带自适应性,可以在有效滤除噪声的同时, 极大程度地保护有用的信息。而且,图像的 NSCT 分解 采用的是具有各向异性的 Contourlet 基,对纹理较丰 富的图像可以更好地发挥自身的多方向选择特性。这一点 可以从图 2(d)和(f)所示的去噪效果对比可以看出, 图 2(f)不仅整体视觉效果好,而且边缘及纹理清晰。

6 结论
本文针对图像去噪信号方差估计往往采用方形窗, 方向选择性差的问题,设计了一种弧形窗口,然后在此 基础之上主要研究了两种图像去噪方法,一种是基于 Curvelet 变换的弧形窗局部 Winner 滤波方法,一种 是基于非下采样 Contourlet 变换的子带自适应阈值去 噪方法,详细阐述了两种去噪算法的公式及步骤,并把 去噪结果和小波变换以及其他相应图像变换下的去噪方法进行了对比,结果表明,本文的方法在保持图像细节 尤其是曲线细节方面有明显优势。
但是,本文仿真试验所用的图像中含有的噪声都是 加性噪声,而没有涉及到乘性噪声,比如医学图像中常 含有的噪声,就是今后我们主要研究的方向之一,另外 应用第二代 Curvelet 变换结合我们设计的弧形窗去噪 时,虽然 PSNR 值较高,但去噪后的图像中有滑痕,影 响了图像质量,如何去掉划痕还有待于进一步研究。
参考文献
[1] A Pizurica,W Philips.Estimating the probability of the presence of a signal of interest in multiresolution single-and multiband image denoising[J].IEEE Transactions on Image Processing,2006,15(3):654-665.
[2] Cunha A.L.da,Zhou J.,and Do M.N.The nonsubsampled contourlet transform:theory,design,and applications[J]. IEEE Transactions on Image Processing,2006,15(10): 3089-3101.
[3] JL Starck,EJ Candes,DL Donoho.The Curvelet Transform for Image Denoising[J].IEEE Transactions on Image
Processing,2002(06):670‒684.
[4] Y Chen,L Lei,ZC Ji,JF Sun.Adaptive Wavelet Threshold for Image Denoising by Exploiting Inter-scale Dependency[C]. International Conference on Intelligent Computing(ICIC 2007)Qingdao(CN),2007.
[5] F Abramovich,T Sapatinas,BW Silverman.Wavelet thresholding via a Bayesian approach[J].Journal of the Royal Statistical Society,1998,60(4):725-749.
[6] Do M.N.and Vetterli M..The contourlet transform:an efficient directional multiresolution image representation [J].IEEE Trans.Image Process,2005,14(12):2091-2106.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/34305.html