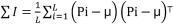SCI论文(www.lunwensci.com):
摘要:散斑干涉的获取的相位条纹图像由于光照条件,摄像设备以及工作环境等因素的影响常常会引入噪音,噪音的存在使得后续的图像分析处理工作难以进行。随着计算力的发展,人工神经网络是近年来兴起的一种新的去噪方法。然而,在应用卷积神经网络进行处理时,由于样本数量的不足,难以获得非常好的效果。本文参考卷积神经网络的工作原理,对去噪卷积神经网络进行了一点改进,在神经网络的前端加入了一个基于噪音估计的学习率计算模块,使得学习过程中神经网络能够更好的学习到噪音特征,将其应用于相位条纹图时获得了不错的效果。
关键词:散斑干涉;噪音估计;卷积神经网络
Convolution Neural Network Image Denoising of Speckle Interferometry Phase Fringe Image Based on Noise Estimation
WANG Xubao,GU Weitao
(Beijing University of Technology,Beijing 100124)
【Abstract】:Speckle interference to obtain the phase stripe image due to light conditions,digital cameras and the working conditions often introduce noise,the influence of such factors as the presence of noise makes it hard for the subsequent image analysis processing work.With the development of computing power,the artificial neural network is in recent years the rise of a new denoising method.However,when the convolutional neural network was used to deal with,because of the inadequate number of samples,is difficult to obtain very good results.In this paper referring to the working principle of convolutional neural network,the denoising convolutional neural network is improved a little,a learning rate calculation module based on noise estimation is added in the front end of the neural network,so that the neural network can better learn the noise characteristics in the learning process,and good results are obtained when it is applied to phase fringe graph.
【Key words】:speckle interferometry;noise estimation;convolutional neural network
0引言
数字图像在采集、传输、处理、储存等过程中常常会产生噪音干扰,因此对图像进行去噪处理获取高质量的图像是后续信息提取必不可少的一环[1]。图像的去噪手段大致可分为几种方法:空间域滤波器[2-5]、频率域滤波器[6-13]、神经网络滤波器等[14-17]。空间域滤波器是最早的滤波器,其主要目的是考察单张图片中像素之间的空间分布关系,依据先验知识设计滤波条件,容易受到局部像素分布的影响。频率域滤波器通过变换域的方式将像素的空间分布处理成频率域分布,能够从总体上较好的把握滤波阈值与效果,但是在原图中本来存在高频变换的区域则容易当成噪音进行误处理。神经网络滤波器是近几年来发展较快的新型处理手段,其中,2008年Jain V[18]等人用卷积神经网络(CNN)处理自然图像的去噪,得到了与常规方法(小波变换法/马尔可夫随机场)相近的结果,这一研究使得CNN进入了图像去噪领域研究人员的法眼,并随之发展出了利用残差神经网络、深度置信网络、循环神经网络等不同神经网络结构对图像进行去噪处理。
基于数据驱动的人工神经网络在训练与测试时会很大程度的受到训练集的影响,因此如何在训练时尽可能的充分利用训练集中信息是研究的一个重点问题,本文考虑利用噪声估计的方法对训练图的质量进行标注,使得神经网络在训练过程中能够充分利用高质量图中的信息而减少低质量图中信息的利用。
1基于主成分分析的噪声估计
一般的图像可以表示为:
Y(X)=S(X)+N(X) (1)
其中,Y(X)是噪音图像,S(X)是原始图像,N(X)是噪音。一般来说噪音符合均值为0方差为σ2的高斯分布。
假设P为矩阵表示的图像块,可将其分为3×3,5×5,7×7,9×9大小等大小不一的图像块,现在求取L个图像块构成的协方差矩阵如下:
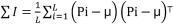
在上式中,Pi表示图片P中的第i个图像块,μ为L个图像块矩阵的均值。
记统计值 r=λmin/σ2 (3)
其中λmin为协方差矩阵ΣI的最小特征值,r无量纲。
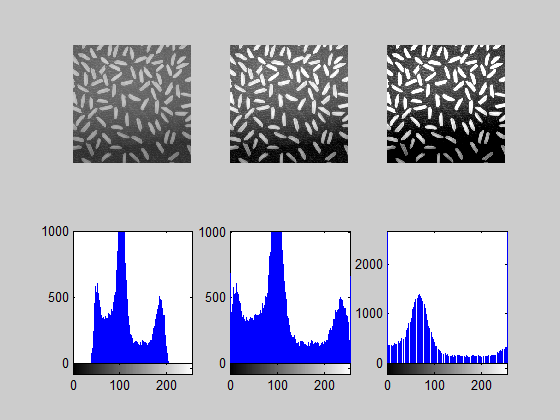
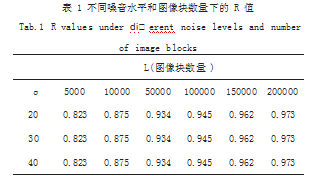
分析多个仿真图像获得结果如表1所示,纵列表示了不同的仿真噪音水平,横列表示了不同的图像块数量,交叉点为r值。
表1中反应了不同噪音水平与图像块数量下r值的依赖关系,可以明显的看出噪音水平的多少与r的值无明显关系,r的值和图像块的数量则有着密切的相关性,任意选择一个噪音水平,从表1中可作出如图1所示图。
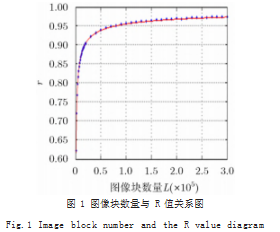
如图1所示,横轴为图像块数量L,纵轴为笔直r,从图像中可以看出,r与L满足一定的非线性分布规律,对上述数据进行分析与拟合后可知r与L满足如下式的回归方程:
r=aLb+1(4)
使用最小二乘法求解此回归方程,两边取对数后,带入数据解得a=-9.6357,b=-0.4589。因此,图片噪音的均方差估计值为:

2网络的构建
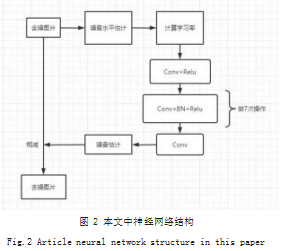
在本文中使用Pytorch进行网络的构建,经过多次的试验,网络的具体结构如图2所示。该网络一共包括9层,第一层为卷积层(Conv)与ReLu激活函数,第二至八层为卷积层加批量标准化(Batch Normalization,BN)加ReLu激活函数,第九层为卷积层。输入的图像被预先裁剪为420×512大小,通过旋转/翻转等方式进行数据增强。所有卷积层中卷积核采用5×5大小的卷积核,学习率的获取依赖于学习率计算模块。训练所用图集为不同噪音水平下的仿真图集,大约1000张图片,按照7:3的比例分为训练集与验证集。
学习率的获取通过几个步骤进行:(1)从训练图集随机选取100张噪音图像。(2)估计100张图像的噪音水平。(3)依据100张图像的噪音水平生成正态分布。(4)在网络获得新图像输入时,估计其噪音水平,并在上述步骤中找到其在累计正态分布中的百分位置。(5)通过下式来计算学习率:学习率=0.002×F(α)。其中F(X)函数为100张图像噪音水平估计获得的累计正态分布,α为新输入图像噪音水平估计在累计正态分布中的百分位。
网络的训练在一台NVIDIA GTX 1660Ti,CPU Core i5 9400F 2.90Ghz,16Gb内存的电脑上完成,python版本为3.6,CUDA版本为10.4。
3训练结果
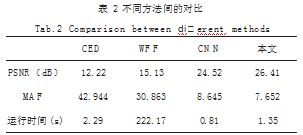
我们将本文的方法与传统的图像处理方法进行了比较,得到了不错的结果。参与比较的方法有增强相空间滤波器(CED)与加窗傅立叶变换(WFF)以及卷积神经网络(CNN)。比较的指标有峰值信噪比(PSNR)平均绝对误差(MAF)以及运行时间上的对比。结果如表2所示。
如表2所示,深度学习的方法在峰值信噪比方面与平均绝对误差方面比传统方法要出色很多,本文的方法基于学习率的改进相比于一般的卷积神经网络更能够学习到图像中的噪音分布,因此比一般的卷积神经网络训练后的效果更好。在运行时间方面,由于本文的方法加入了一个计算学习率的模块,因此每张图片的运行时间比一般的卷积神经网络更长,在之后的工作中可以考虑训练完成后去掉该模块,时间上应该会有所提升。
如图3所示展示了本文与其他方法在相位图像去噪以及提取骨架线方面的比较。上半部分图像为相位条纹图,下半部分图像为其提取的骨架线。
从图3中可以看出,传统方法在不同程度上存在模糊以及伪影问题。(图3中a1表示了使用本文方法去噪后的相位条纹图,a2表示了使用本文方法去噪后的骨架线提取图,b1,b2表示了未去噪前的相位条纹图,c1表示了使用WFF方法去噪后的相位条纹图,c2表示了使用WFF方法去噪后的骨架线提取图,d1表示了使用CED方法去噪后的相位条纹图,d2表示了使用CED方法去噪后的骨架线提取图,f1表示了使用CNN方法去噪后的相位条纹图,f2表示了使用CNN方法去噪后的骨架线提取图。)
使用CED方法的图像在处理后高频区域内十分混乱,骨架线的提取存在大量的断裂。使用WFF方法处理的图像虽然减少了骨架线的断裂,但是在高频区域内存在模糊/对比度低的问题,这使得人们难以从图像中获取清晰的相位分布情况。本文以及CNN方法则较好的去除了噪音,同时也良好的保留了骨架线,对进一步的获取相位信息提供了帮助。
4结语
本文提出了一种基于噪音估计的卷积神经网络去相位条纹图方法。相比于传统去噪手段,本文的去噪手段效果更优质,所需时间更短,实时性更好。训练完成后具有一定的迁移能力,可以扩展到其他相位条纹图像的去噪中去,如全息相位干涉图等。
参考文献
[1]张娜娜,张媛媛,丁维奇.经典图像去噪方法研究综述[J].化工自动化及仪表,2021,48(5):409-412+423.
[2]齐德明.基于改进型的非局部均值滤波算法在医学图像处理中的研究与应用[J].计算机应用与软件,2021,38(9):256-261+279.
[3]郑宏亮,王奕,张天壮,等.快速二步交叉非局部的图像混合噪声滤波器[J].吉林大学学报(信息科学版),2021,39(5):498-503.
[4]陈伟,党榕.混合噪声图像的去噪算法研究及FPGA实现[J].电子测量技术,2021,44(16):135-140.
[5]谭宏伟,周芳,贺丰收.一种基于相位补偿的干涉图自适应滤波算法[J].遥感信息,2021,36(4):55-62.
[6]文鸿雁,郭锴,陈伟清.基于遥感图像频率域滤波的灰色线性中值去噪算法[J].桂林理工大学学报,2014,34(4):697-703.
[7]裴建隆,朱煜峰.不同频率域滤波器的去噪效果比较分析[J].江西科学,2019,37(4):609-614.
[8]Bo L,Cheng W,Peisheng M,et al.Fingerprint image enhancement using mixedfilters[J].Journal of Computer Applications,2008,28(7):1892-1895.
[9]刘长波.基于稀疏表示和频域方向滤波的图像雨雪去除算法[D].天津:天津大学,2014.
[10]李世金,张书毕,张秋昭,等.自适应伪相干值改进的InSAR干涉图Goldstein滤波算法[J].金属矿山,2018(7):152-156.
[11]陆达,邬敏贤,金国藩.计算全息术中的空间域滤波[J].光学学报,1986(1):87-92.
[12]杨超.时频域结合的数字图像增强技术的研究[D].唐山:华北理工大学,2019.
[13]高延东.面向高精度DEM的InSAR关键处理技术研究[D].徐州:中国矿业大学,2019.
[14]Kai Z,Wangmeng Z,Yujin C,et al.Beyond a Gaussian Denoiser:Residual Learning of Deep CNN for Image Denoising[J].IEEE Transactions on Image Processing,2017,26(7):3142-3155.
[15]Kai Z,Wangmeng Z,Lei Z.FFDNet:Toward a Fast and Flexible Solution for CNN based Image Denoising[J].IEEE transactions on image processing,2017:1.
[16]Shi G,Yan Z,Kai Z,et al.Toward Convolutional Blind Denoising of Real Photographs[J].2018.
[17]Danelljan M,Hger G,Khan F S,et al.Learning Spatially Regularized Correlation Filters for Visual Tracking[J].CoRR,2016.
[18]Jain V,Seung H S.Natural Image Denoising with Convolutional Networks[C].International Conference on Neural Information Processing Systems.Curran Associates Inc,2008.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/39114.html