摘要:随着人工智能及脑科学的发展,深度学习逐渐成为一个研究热点。在教育领域,深度学习有助于学生扎实掌握学习内容,发展高阶思维,培养核心素养。而单元教学是连接深度教学和深度学习的“桥梁”。基于此,文章以“一次函数”为例,围绕单元教学论述了引导学生深度学习的教学策略。
关键词:初中数学,深度教学,单元教学
教材是实施教学的依据。根据知识点在整个教学体系中的作用和学生的心理发展规律,华东师大版数学教材组建了不同的单元,指引教师进行单元教学。然而,在数学教学实践中,部分教师虽然能从整体角度定位知识,但仍一味采取传统的单课时教学方式,导致学生很难把握知识点之间的联系,容易出现知识碎片化、学习表层化的问题,同时,学生也难以将知识内化为自己的理解,灵活地迁移、应用数学知识。解决这些问题,需要引入单元教学。单元教学以单元为教学单位,注重宏观把控,能够弥补单课时教学的不足,助推学生深度学习,是深度教学和深度学习之间的“桥梁”。因此,教师要站在深度教学视域下,着力实施数学单元教学,促进学生的深度学习。
一、深度教学视域下的初中数学单元教学概述
(一)深度教学
深度教学是深度学习在教育领域发展的结果。深度教学是展现知识生产过程,剖析知识外部符号与内部逻辑关系,使学生建立知识之间的内部联系与整体知识结构,获取数学思维方法,继而在新情境中解决数学问题,发展高阶思维的教学活动[1]。
(二)单元教学
单元教学是指站在整体视角,整合不同版本教材中具有逻辑性的内容,形成新的教学单元,并以此为基础,制订单元教学目标,划定课时安排,实践教学流程,并在教学过程中进行效果评价,获得最高价值的动态循环的教学过程。
(三)深度教学视域下的单元教学
深度教学视域下的单元教学是以深度教学理念为指导,以单元教学为载体,促使学生进行结构性分析,建构知识体系,获取数学思维方法,锻炼高阶思维,发展核心素养的教学活动。
在深度教学视域下实施数学单元教学时,教师要站在整体角度,整合教学内容,构建新的教学单元,再以新的教学单元为基础,紧扣学生的深度学习进行教学目标设计,依据单元内容之间的联系划定教学课时,最后以数学课堂为依托,应用多种方式组织教学活动,引导学生深度学习。
二、深度教学视域下的初中数学单元的具体教学策略
下文将以“一次函数”为例,论述在深度教学视域下实施单元教学的策略。
(一)整合教学内容,建构教学单元
建构教学单元是实施单元教学的基础。教师要打破教材单元或版本的限制,探索不同知识点之间的联系,建构新的教学单元,夯实深度教学基础。
“一次函数”在华东师大版数学教材中位于八年级(下册)第二单元,本单元共五节,即“变量与函数”“函数的图像”“一次函数”“反比例函数”和“实践与探索”。其中,“一次函数”是本单元的教学重点,包括“一次函数”“一次函数的图像”“一次函数的性质”和“一次函数的表达式”。在分析华东师大版数学教材内容的同时,教师可以重新整合教学内容,建构出“一次函数”新单元。单元内容有“变量与函数”“函数的图像”“正比例函数”“一次函数”“反比例函数”“一次函数与方程、不等式”和“实践与探索”。这样的教学内容,便于学生进行结构性分析,把握不同知识点及其之间的联系,建构知识体系,扩展学习深度。
(二)紧扣深度学习,设定教学目标
教学目标是单元教学的指引。与单课时教学相比,深度教学视域下的单元教学不是只让学生机械地记忆、理解、掌握知识,而是让学生在掌握知识与技能的基础上,发现数学本质,获取数学思维方法,感受数学的价值和意义,反思数学知识与问题[2]。这一过程,正是学生进行深度学习的过程。因此,教师要紧扣学生的深度学习,结合单元教学内容,设定相应的教学目标。
“一次函数”的单元教学目标如下:
(1)经历数学问题探究过程,发现其中的变量关系和变化规律,建立函数模型,解决实际问题,认知函数的本质,体会函数的应用价值。
(2)分析实际案例,利用表格法、解析式法、图像法解决问题,体会函数的本质,并根据不同的函数形式探索函数关系与变化规律。
(3)解决实际问题,根据具体情况判断函数自变量的取值范围,确定函数值;对比函数的三种形式,明晰各自的优势和劣势。
(4)利用描点法绘制函数图像,明晰一次函数、正比例函数、反比例函数的图像特征;根据函数图像,归纳、总结函数性质;根据函数图像判断函数值的增减情况,感受数形结合法。
(5)分析一次函数图像,获取关键信息,确定一次函数解析式(待定系数法),解决实际问题,体会数形结合法的意义。
(6)对比、分析一次函数、一元一次方程、二元一次方程组、一元一次不等式,把握它们之间的关系,以函数变化视角反思不等式与方程,建立知识体系。
(7)剖析实际问题,建立一次函数模型,获取数学建模思想方法,锻炼问题解决能力,学会用函数的思想分析、解决现实问题。
(三)把握知识联系,分配单元课时
课时教学是落实单元教学的途径。与传统的单课时教学相比,单元教学下的课时教学之间有着密切的联系,构成了统一的教学整体。知识联系是单元课时的切入点,有联系的知识点便于学生逐步深入探究,拓展学习深度和广度。因此,在深度教学视域下实施单元教学时,教师要依据知识间的联系分配单元课时。
掌握函数的概念是学生学习正反比例函数和一次函数的基础。学生在学习正反比例函数和一次函数后,可以对比不同的函数、不等式、方程,掌握知识点之间的联系。基于此,教师可分配如下的单元课时内容(见表1):
(四)依托数学课堂,开展深度教学
课堂是开展深度教学的平台。在数学课堂上,教师要结合教学目标和课时内容,依据深度教学特点组织教学活动,引导学生深度学习。
1.创设情境,调动兴趣
建构主义理论指出,有效的学习情境利于学生进行意义建构。与此一致的是,深度教学的核心策略之一正是创设教学情境[3]。因此,在实施课堂教学时,教师要围绕数学教学内容,创设教学情境,调动学生兴趣,夯实深度教学的基础。
例如,在“函数的概念(一)”课堂教学中,教师要依据现实生活和教学内容创设生活情境。具体而言,教师可以借助电子白板展示实际生活中关于运动与变化的现象,如“地球在整个宇宙中的位置随着时间的变化而变化”“气温随着海拔的增高而降低”“弹簧随着拉力的增大而伸长”等。大部分学生会认真观察这些现象,也会自发迁移生活经验,思索各种现象中的变化量。如此,有学生会发现“变化过程中必然存在两个变量间的依存关系”的规律。教师趁机引出本节课内容,和学生一起探究变化量之间的变动规律。学生的学习兴趣愈加浓厚,能够主动走进数学课堂。
2.提出问题,驱动探究
深度教学的核心理念是问题引领,多层次分析、理解知识[4]。深度教学是体验性、理解性的教学。在深度教学过程中,学生会发挥主观能动性,不断迁移认知、解决问题,由此理解数学知识,发现数学本质,用数学的语言进行表达。在数学课堂上,教师要依据数学教学内容,提出具有引领性的问题,驱动学生深入探究。
例如,在“函数的概念(一)”这节课上,为使学生认知函数概念,教师呈现不同的实例,并提出问题,引导学生分析两个变量之间的关系。
实例1:轻轨的运行速度是60 km/h(停靠站的时间忽略不计)。假设轻轨的行驶路程为s(km),行驶时间为t(h)。请问,轻轨运行的路程和时间之间有怎样的关系?假设任意确定一个时间t,是否能确定t所对应的路程s?
实例2:在举办元旦晚会之前,所有班级都购买了不同数量的荧光棒。其中,一班购买了56根,二班购买了67根,三班购买了45根。假设每根荧光棒2元,请问这些班级购买荧光棒各自花费多少钱?若某班决定购买x根荧光棒,要支出的班费为y元,x与y之间有怎样的关系?
实例3:某市的自来水价格为3.5元/吨。假设某户人家每月用水量为m(吨),水费为n(元)。请问,用水量m和水费n之间有怎样的关系?
学生纷纷开动脑筋,认真阅读题目,把握关键信息,列出关系式。这时,教师引导学生思考:“在以上实例中,有哪些量是变化的,有哪些量是始终不变的?”学生继续分析,将视线集中在变量和常量上,并主动作答。依据学生的作答情况,教师概述常量和变量的内涵。在学生建立一定的认知后,教师继续提问:“在这些变化过程中,有多少个变量?变量之间有怎样的关系?”学生认真观察、对比每个实例,以发现变量之间的关系。有的学生提道:“当一个变量发生变化时,另外一个变量也在发生变化。”基于此,教师提问:“当其中一个变量取定值时,另外一个变量是否确定?”学生继续思索,探寻变量之间的关系。最后,教师依据学生的探究成果,展示函数概念。通过从具体到抽象、从特殊到一般的分析过程,学生能够用数学的思维进行分析,用数学的语言进行表达,有利于增强深度学习效果。
3.随堂练习,迁移应用
深度教学的特点之一是学生迁移应用[5]。迁移应用既是学生建构新旧知识间的联系,建立知识结构的方式,又是学生解决问题,巩固课堂所学的途径。在数学课堂上,学生能够在教师的引导下,不断迁移应用已有认知,解决问题,掌握新知。教师要把握时机,组织随堂练习活动,引导学生迁移应用,解决实际问题。在迁移应用的过程中,学生可以在了解自身学习情况的基础上达到查漏补缺的目的。
例如,在“一次函数的概念(一)”这节课上,教师结合函数概念以及学生之间的学习差异,设计难度不同的随堂练习,如:
练习一:请分析课堂上展示的三个实例,写出它们的函数关系式,并指明自变量。
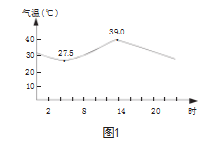
练习二:图1是本地夏季某天的气温变化图。横坐标表示时间,纵坐标表示气温。请问,时间和气温之间是否构成函数?为什么?
练习三:请用自己的话描述函数概念,并联想生活经历,列举满足函数关系的实例。
在完成练习题时,学生迁移课堂认知,列出函数关系式,分析变量之间的变化规律,增强对所学内容的理解。不少学生会因此调整原有认知结构,建构知识体系,感受函数的应用价值,锻炼数学思维能力。
三、结束语
总之,在深度教学下实施单元教学,可以使学生深度学习单元内容,提高数学学习效果。对此,在实施数学单元教学时,教师要以深度教学理念为指导,整合教学内容,设定教学目标,合理分配课时,以数学课堂为平台,应用多种教学方式来引导学生发挥能动性,不断迁移应用已有认知,解决问题,理解学习内容,更新知识结构,锻炼多种能力,提升课堂学习效果。
参考文献
[1]萧明正.基于深度学习的初中数学单元主题式教学策略[J].亚太教育,2022(18):87-89.
[2]顾晓宇.基于深度学习的初中数学单元教学设计研究[D].上海:上海师范大学,2022.
[3]万兵.基于深度学习的初中数学单元教学研究[D].武汉:华中师范大学,2022.
[4]陈庆.基于深度学习的初中数学单元整体教学研究[D].福州:福建师范大学,2021.
[5]金渝超.深度教学视角下的初中数学单元教学设计研究[D].重庆:西南大学,2021.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/79233.html