SCI论文(www.lunwensci.com):
摘 要 : 文章通过设计由浅入深的课堂活动,引导学生通过探究实践,提升数学思维能力,发展 核心素养,实现深度学习.
关键词 : 活动设计; 深度学习; 平面直角坐标系
深度学习是指在教师引领下,学生围绕着具有 挑战性的学习主题,全身心积极参与、体验成功、获 得发展的有意义的学习过程[1].要实现深度学习, 学生要对问题本身进行全面、深入、完整的理解.同 时,还要理解与其相关的背景、环境等因素.在深度 学习中,学生能关联相应事物所有要素,深入事物核 心,能对事物的本质有一个较清晰地认识.传统的课 堂学习大多是“脖子以上的学习”为主,动用的多是 听觉和视觉.深度学习应该是让学生全方位地感知 世界,最大化地让学生用身体“五觉”完整地感受事 物[2],让学生用身心体验学习,促使学生对多种感 官的综合应用,同时这种参与和学习必须是具有自 发性、自主性,充满热情的.
新课程教学背景下,教师必须立足于学生的发 展来设计数学教学活动,使学生通过生动有趣的活 动载体,将新的知识融入原有的知识结构中,实现发 展高阶思维,知识发生新的迁移,从而提升数学学科 核心素养,实现深度学习.
1 平面直角坐标系教学思路的设计
教学思路设计是对所教内容的认识,对整堂课 设计的思考即 : 教学目标、教学途径、教学方法与措施、如何突出重点、如何分散难点等.只有科学的教 学思路,才能使数学学习符合学生的发展规律.
笔者认为,必须遵循《数学课程标准》的要求. “为学生的发展而教” ,必须把教学的最根本出发点 放在学生的发展上,突出基础性、普及性、发展性,使 数学教育真正做到面向全体学生.因此,教学总体思 路设计 : 第一,教学的重点是“导”学,先让学生“学” 数学,再由教师“教”数学 ; 第二,在组织学生进行学 习活动时扮演指导者的角色 ; 第三,注重数学思想的 培养,逻辑思维能力的训练 ; 第四,学习数学基础知 识、训练数学基本能力不能有丝毫松懈 ; 第五,实行 差异性教学,让每个人都能习得必要的数学,并有区 别地发展.
本节课学习“平面直角坐标系 ” ,让点与坐标的 对应顺利实现一维到二维的跨越.“平面直角坐标 系”就是“数轴”的发展.“平面直角坐标系”的建立, 使有序数对与坐标平面内的点一一对应,是数形转 化的基础,是沟通代数与几何的桥梁,是学生今后学习 函数、函数与方程、函数与不等式关系的基础知识.
上一节课学生对“有序数对表示物体的位置” 在具体情境中进行了学习.本节课先复习回忆数轴 上点与实数的一一对应,并发现平面上的位置无法用一条数轴来准确描述,在此基础上说明建立平面 直角坐标系的必要性以及合理性.我们引入平面直 角坐标系用于平面上任意一个位置的描述,也就是 本节课的教学重点: 已知点的坐标在平面直角坐标系 中描点,和由平面直角坐标系内的点的位置写出它的 坐标.然后我们再进一步深入讨论各象限的符号特征.
学生经历画坐标系、描点、看图、观察、总结归纳 点的特征等活动过程,使学生能够通过坐标准确描 出点的位置、通过点的位置写出点的坐标、通过点的 坐标特征判断点的位置等,感受“数形结合”“从特 殊到一般”的数学思想,体会从具体到抽象的认知 规律,初步体验将实际问题数学化的过程和方法.
2 平面直角坐标系教学过程的活动设计
教学过程的设计体现教师的教学思想、教学手 段和方法以及艺术水平.课堂活动既能活跃课堂气 氛,激发学生兴趣,还能直击学生的心灵,诱发深度 思考,开发学生智能,碰撞思维的火花,实现师与生、 生与生的情感交流.教学活动设置的优劣对一堂课 的成败起着举足轻重的作用.
本节课一共设置三个大环节的活动.
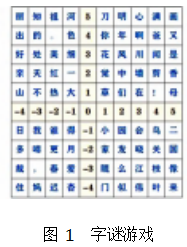
第一个大环节 : 复习引入,创设情境.又设置了 两个小环节: 第一个是复习回忆数轴相关知识,包括它 的三要素,以此给学生烙印本节课第一个“一一对应” ; 第二个是字谜游戏,复习上节课平面上的位置与有序 数对的对应关系,给学生烙印第二个“一一对应”.
如图 1,“家”字的位置记作( 1,-2) ,请你破解 密码: (-3,-1) ( -1,-3) ( 1,4) ( -3,-3) (2,2) (5,-2) (4,1).密码 : 我爱你,中国!
你能在里面找到一句你熟悉的诗句吗? 请把它 用密码表示出来.
设计意图 : 通过密码游戏,使学生直观理解“位置”与“有序数对”间 的“一一对应”关系,为 引入 “平面直角坐标系”埋伏笔.通过找诗句,加强学科 间的融合,渗透全面发展的重要性,同时增加了课堂 趣味性.
第二个大环节 : 探究新课、巩固新知,设置了四 个小环节.
第一个小环节 : 知识点( 1) 平面直角坐标系
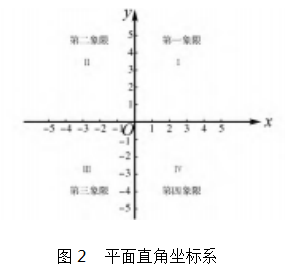
用到前面的铺垫,如何描述平面中任意一点的 位置? 显然一条数轴已经无法达到目的,因此我们 类比数轴和字谜游戏引导学生抽象概括出平面直角 坐标系及其相关概念,由教师示范画出平面直角坐 标系( 图 2).紧接着让学生在暗格上模仿画一个平 面直角坐标系,并标出相应的元素.这里学生特别容 易漏画箭头也就是正方向.
请大家类比数轴,我们要将平面直角坐标系画 成什么样子?
①说一说组成平面直角坐标系的两条数轴具备 什么特征? ( 互相垂直,原点重合 ; 每一条数轴上也 有正方向、单位长度、原点) 由我们的生活经验,向 上为正,向下为负.
②两条数轴分别叫什么名字? 交 点叫什么? ( 水平的为 x 轴或横轴,竖直的为 y 轴或 纵轴,交点仍然叫原点) .
③用来表示平面上的点的有序数对,叫什么?
④平面被两条坐标轴分成了几个部分,分别叫 什么?
第二个小环节 : 知识点(2 ) 已知坐标确定点的 位置
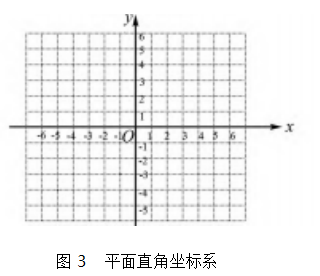
在画好的平面直角坐标系( 图 3) 中根据点的坐 标,找点的位置.此时特别注意演示 : 要找到横坐标 对应的列,纵坐标对应的行,也就是过横纵坐标分别 向 x 轴、y 轴作垂线,交点即是该点的位置.接下来让学生亲历描点过程,体会对应关系.
第三个小环节 : 知识点(3 ) 确定直角坐标系中 点的坐标的特征
请观察你刚描点的象限及他们的坐标,是否能 找到他们的一些共同特征? ( 见表 1)
进一步追问: ( 1) 如果点 P(x,y) 在第二象限, 那么 x,y 分别是正数还是负数?
(2) 如果 x>0,y<0,那么点 P(x,y) 在第几象限?
在第二个环节的基础上,我们进行点的分类,并 通过问题串的形式引导学生观察分类后的点的坐标 有什么共同特点,它们为什么会具有这样的共同特 点? 比如第一象限的点 A,它的横纵坐标对应的就 是 x 轴和 y 轴正半轴上的数,最后它落在第一象限, 那所有在第一象限内的点的横纵坐标是不是都为正 数? 从而使学生进一步内化“数形结合”思想,最后 用几何画板来检验我们所得结论.紧接着我设置了 三个小题和两个小游戏,一是为了活跃课堂气氛,二 是检验学生刚才那一番“内化”有没有真正吸收.其 中第 4 题为了培养学生的符号意识,体现特征的普 遍性,让学生熟悉用符号表达和描述问题,体会从特 殊到一般的数学思想方法.第 5 题是一道简单的含 参问题,本质还是考察特殊位置的点的坐标特征.
第四个小环节 : 知识点(4) 已知点确定坐标巩固第三环节的果实,由点的位置写出点的坐 标.先判断其所在象限,再来一番刚才描点的逆操 作,分别向 x 轴和 y 轴做垂线,找到其对应两轴上的 坐标.特别提醒学生,要将横坐标也就是 x 轴上的坐 标写在前面,纵坐标写在后,中间用逗号隔开.
至此本节课的重难点都基本结束,进入我们第 三个大环节 : 课堂小结,回顾提升.通过问题串实现 对本节课知识点的回顾,最后引出大鼻子笛卡尔,是 他最早引入坐标系,当然我们现在学习的是前人在 他的基础上不断完善的结果,但是这种用代数的方 法来研究几何图形的“数形结合”的思想,是我们今 后学习经常用到的数学思想方法.
3 有关平面直角坐标系的典型练习题的设置
练习 1 请大家在导学案上自己画一个平面直 角坐标系,并标出象限和横轴、纵轴和原点.
设计意图 学生自主作图,可以充分考查其对 知识的理解,检测是否会独立而完整地画出直角坐 标系,正确标明坐标系的原点、正方向和单位长度, 亲自经历的过程就是学生将知识内化的过程,能够 正确且准确地画出平面直角坐标系,将为后续函数 的学习提供有力的保障.
练习 2 请在你画好的平面直角坐标系中描出 下列各点 :A(4,5) ,B( -2,3) ,C( -4,-1) ,D(2. 5,-4) ,E(0,-4) ,F(0,5) ,G( -3,0) ,H( 1.5,0) . 并指出它们分别属于哪个象限.
设计意图 ( 1 ) 从 用“有序 数对”表示 具体 物体的位置,点的坐标则是其进一步抽象,学生 是否真的理解了,自主而准确地标注点坐标显得 尤为重要.这也是本节课的重点.(2 ) 通过标注点 坐标,引导学生观察点坐标的特征,为后续探 究 象限特征做铺垫.
参考文献 :
[1]刘月霞,郭华.深度学习走向核心素养(理论普及 读本) [M].北京:教育科学出版社,2018 :32.
[2] 张宏伟.如何理解学生的深度学习[N].中国教 师报,2020-07 -15(4) .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/75171.html