SCI论文(www.lunwensci.com)
摘 要 : 一元一次方程是初中数学的重要知识点,是解决应用题的常用工具.为掌握不同类型 应用题解题方法,提高一元一次方程应用题解题效率,应针对不同应用题类型,采取不同的授课方法,这也是学生把握破题的关键.
关键词 : 初中数学; 应用题; 一元一次方程
一元一次方程应用题主要有配套问题、工程问 题、盈亏问题、方案问题、行程问题和几何问题[1]. 列一元一次方程的关键在于寻找到等量关系,教学 实践中应将抽象问题具体化,帮助学生理解、寻找等量关系,提高其应用一元一次方程的解题技能.
1 配套问题
配套问题在初中数学中较为常见,创设的情境 描述的是整体与局部的关系[2].寻找等量关系可从时间、参与人数总量入手.
例 1 某生产厂家设计一种储物柜.每个储物 柜由两扇门、三个抽屉、一个框架构成.一个工人每 天可以做 5 扇门或者 3 个抽屉或者 2 个框架.如果 共有 38 名工人,要求全部参加工作,如何分配可使 得工人每天的工作刚好能配套完成一定数量的柜子,并计算每天完成柜子的数量.
该情境中柜子、框架、抽屉、门之间存在隐含的 等量关系,只要设出其中一个变量,则可顺利地表示出剩余变量.同时要求学生思考工人数量与对应部件间的对应关系,构建一元一次方程.解析 设参加制作框架的工人为 x 人,则每天 制作的框架数量为 2x 个.要想配套则需要制作 2x 个柜子,对应需要 6x 个抽屉,4x 扇门.制作抽屉和 门的工人分别为6x/= 2x 人、4x/5= 0.8x 人,工人总数 为 38 人,则可列出一元一次方程为 : x + 2x + 0.8x = 38.解得 x = 10.则做框架、做门和做抽屉的工作分别为 10 人、8 人、20 人,每天恰好制作 20 个柜子.
2 工程问题
工程问题是初中数学中极为常见的问题.解答 该类问题的难点在于如何理解每天工作量和天数之 间的关系.很多学生不明白为什么将总工程量看做 “1”.为帮助学生更好地突破这一难点,应以学生熟 悉的生活情境为切入点,对工作效率加以解释,即将 整个工程量看做 1.则每天完成的工作量为 1/天 数[3].在此基础上为使学生活学活用,应做好例题展示,看其能否正确回答.
例 2 某道路改造工程由 1 号单位施工计划 30天能够完成,结果在施工 10 天时接到通知需要提前8 天完成工程.为完成施工要求剩余工程由 1 号和 2号单位共同完成,结果如期完成施工任务.
( 1) 若要求 2 号单位单独完成该工程,需要多少天?
(2) 若 1 号和 2 号单位同时进场,完成整个工程需要多少天?
围绕问题情境设计如下问题 :
( 1) 1 号单位的工作效率是多少?
(2) 接到通知时 1 号单位完成的工程量该怎么表示?
(3) 两单位合作的天数是多少? 搞清楚者三个问题便不难列出正确的一元一次方程.根据题干描述还需明白两个单位合作的过程中 1 号单位的工作效率并未发生改变,认识到这一点从 2 号单位的工作效率入手问题便迎刃而解.解析 ( 1) 设 2 号施工单位每天的施工量为 x, 1 号施工单位按照计划每天的施工量为1/30.施工 10 天后接下来还需施工 30 -8 -10 = 12 天.2 号单 位同样需要施工 12 天.则列一元一次方程式为 : 1/30× 10 +1/30 × 12 + x × 12 = 1.解得 x = 1/45.则 2 号单位单独完成该工程需要 45 天.
(2) 设两单位共同完成该工程需 x 天,则(1/30+1/45) x = 1.解 得 x = 18.即两个单位共同施工需18 天.
3 盈亏问题
盈亏问题与人们的生活密切相关,多数应用题 情境都来源于人们的生活.运用一元一次方程解答 该类应用题的关键在于明确成本、售价、利润、打折 之间的关系,尤其借助百分比和成本表示售价时应 能正确表示出来,明白打折就是按照对应价格的百分之多少出售.
例 3 某商店出售甲、乙两种商品.两种商品的
成本总价为 300 元.其中甲、乙商品分别按照 60% 、 50% 的利润率出售.销售过程中均按照标价 9 折出 售,该商店总获利 114 元.
( 1) 甲、乙两种商品的成本各多少元?
(2) 若该商店投入 1 000 元购进这两种商品,每种商品至少购进 1 个,则如何安排进货获利最大?
情境中给出两种商品的成本价之和以及出售规 则.授课时要求学生从甲、乙商品中的其中一个商品 入手设参数,看其能否正确表示出售价格,以及如何围绕“114 元”构建一元一次方程.
解析 ( 1 ) 设甲商品的成本价为 x 元,则乙商 品的成本价为(300-x) 元,则对应的标价分别为( 1 + 60% ) x,(300-x) ( 1 + 50% ) ,则根据题意可列一 元一次方程 : 0.9 ( 1 + 60% ) x + 0.9 (300 -x) ( 1 + 50% ) -300 = 114.解得 x = 100.则甲、乙两种商品 的成本分别为 100 元、200 元.(2) 根据题意甲、乙两 种商品的利润分别为 0.9 ( 1 + 60% ) × 100 -100 = 44 元,0.9 × ( 1 + 50% ) × 200 -200 = 70 元,相当于 花费 100 元利润为 35 元.显然进的甲商品越多,获利越多,则乙商品只进 1 个,甲商品进 8 个.
4 方案问题
方案问题往往给出多个方案,要求学生选择最 佳方案.吃透题意,寻找参数的对应关系是解题的关 键.为提高学生条理分析问题的意识与能力,要求学 生在读题后,要对题干中的“关键词”进行分类,分别寻找等量关系.
例 4 使用甲、乙两种车运送货物.两车同时参 与运输需各运 12 趟,支付 4 800 元费用.若甲、乙两 车均单独运完,则乙车运输趟数是甲车的两倍,且乙车每趟运费比甲车少 100 元.
( 1) 甲、乙两车每趟的运费是多少?
(2) 若仅使用一种车,甲、乙两车每趟还需分别 支付 40 元,20 元的损失费,单独使用哪辆车运完该批货物支出的总费较少,总费用是多少?
情境中涉及两个非常重要 的关键词“运 费”“趟数”.其 中 围绕“总运 费”“ 甲乙运费的关系 ”可列出对应的一元一次方程.围绕“两车单独运 输的趟数”以及 隐含 的工程量为“1 ”可列 出对应 一元一次方程,求出参数后计算出单独使用甲、乙的总费用.
解析 ( 1 ) 设甲车每趟的费用为 x 元,则乙车 的费用为(x -100) 元,根据题意可得 12x + 12 (x - 100) = 4 800.解得 x = 250.则甲、乙两车的运费分别 为 250 元,150 元.(2) 单独使用甲车需运输 y 趟,则乙车需 2y 趟,根据题意 12/y+12/2y= 1.解得 y = 18.经检验 y = 18 为原方程的解,2y = 36.单独使用甲车的 费用为(250 + 40) × 18 = 5 220 元,单独使用乙车的 费用为( 150 + 20) × 36 = 6 120 元,显然单独使用甲 车的总费用最少,为 5 220 元.
5 行程问题
行程问题是初中数学中一类结合实际且较有意 思的问题[4].部分习题以图象设问兼顾考查学生的 读图能力,解题的关键在于吃透图象纵轴、横轴表示的含义,明确变化点表示的含义.
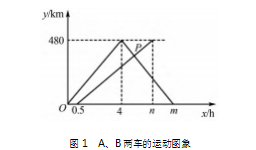
例 5 甲、乙两地相距为 480 km,A、B 两车分别 从甲乙两点开始相向而行,A 车到达乙地立即返回, B 车到达甲地停止.其中 B 车的速度为80 km / h.两 车离各自出发地的距离 y( km) 和行驶时间 x( h) 之 间的关系如图 1 所示.
( 1) 图中 m、n 的值分别是多少?
(2) 求出 P 点坐标,并解释该点的实际意义.
图象中的隐含信息较多,学生需根据题干描述 将 A、B 两车的运动图象对应起来.两个图线的起始 点并不相同,意味着 A、B 两车并不是在同一时间出发的,这一点应给予学生引导使其引起足够重视,如可询问其哪辆车先出发,哪辆车后出发中间相隔多长时间等.
解析 ( 1) 根据题干描述折线为 A 车的运动图 象,直线为 B 车的运动图象.由图像知 A 车单程用 时 4 小时,则双程用时 8 h.B 车速度为 80 km,用时 480 ÷ 80 = 6 h,则 m = 8.n = 6.5; (2) P 点表示 A 车 返回甲地时距甲地的距离和 B 车距离乙地的距离 相等.由 ( 1 ) 可 知 A 车 的运 动 速 度 为 480 ÷ 4 = 120 km / h.设 A 车行驶时间为 x h,2 × 480 -120x = 80(x-0.5) 解得 x = 5.则 80 × (5-0.5) = 360.则 P 点坐标为(5.360).P 点表示的意义为 A 车行驶 5 h 后 A、B 两车距离各自出发点的距离为 360 km.
6 几何问题
部分几何类的应用题需运用一元一次方程知识 解答.解答几何类应用题常需画出草图以更好地揭 示相关参数之间的内在关系,但是部分习题围绕 “距离”设计的有陷阱,使学生难以识别.为提高学 生解题的正确性,应为其剖析“陷阱”设在何处,如 何加以识别,尤其通过展示应用题的具体解题过程, 启发其在以后列一元一次方程时能更为全面地考虑问题.
综上所述,用一元一次方程解应用题时应做好 题型的归类,并做好不同题型解题方法的探寻、应用以及总结.
参考文献 :
[1]石莲花.核心素养视域下初中数学应用题教学 的实践与探索 : 以“一元一次方程的应用”教学 为例[J].现代教学,2022 (09) : 63-64 .
[2]梁飞.提升一元一次方程应用题教学效果的三个策略[J].广西教育,2021 (01) : 121.123 .
[3]范志德.关于初中数学一元一次方程应用解题 研究[J].天津教育,2019(33) : 155 -156 .
[4]丁丽娟.初中数学一元一次方程应用题解题研 究[J].中学数学,2019(16) : 63-64 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/75069.html