SCI论文(www.lunwensci.com):
摘 要 : 在新课程改革持续推进的教育背景下,对高中数学教学提出更高的标准和要求,不仅 要关注理论知识、运算方法和解题技巧,还需要注重学生思维能力的培养与发展.教师在教学中需 探寻有效途径培养学生的逆向思维,将学生逆向思维的培养融入点滴教学之中,在促进学生思维品 质提升的同时,使其深化理解与掌握数学知识及技能.
关键词 : 有效途径; 课堂教学; 逆向思维
逆向思维又称之为求异思维,即为对司空见惯、 似乎已成定论的事物或观点反过来思考的一种思维 方式,使思维向对立面的方向发展,从问题的相反面 深入探索,树立新思想和创立新形象.高中数学作为 一门逻辑思维和抽象性十分强的科目,逆向思维成 为高中生学习数学知识与解题的必备品质之一.在 高中数学教学中,教师要将培养学生逆向思维的品 质融于平时的数学教学中,不断关注学生的思维能 力发展,通过探寻有效途径加大培养力度,从而既优 化学生的思维品质,又促进学生数学能力的飞跃.
1 基于概念教学着手,培养学生逆向思维
在高中数学课程教学中,概念属于基础性知识, 是学生学习其他知识和解题的前提.为有效培养学 生的逆向思维,教师首先可基于概念教学着手,使其 对概念进行反向推理,潜移默化地培养逆向思维.对 此,高中数学教师在概念教学中,不能因循守旧地只 带领学生进行正向推导,还要指导学生学会反向推 理,使其数学思维不再固化,而是变得发散和开阔.
在进行“对数函数”教学时,教师先带领学生回 顾指数函数的研究过程,再次谈论细胞分裂问题,学生知道某种细胞分裂时,得到细胞个数 y 是分裂次 数 x 的函数,可用指数函数 y = 2x 表示.接着,教师设 疑 : 现在大家一起从逆向视角研究相反的问题,假如 要求这种细胞经过多少次分裂,大约可以得到 1 万 个,10 万个…… 细胞,那么分裂次数 x 就是要得到 细胞个数 y 的函数,根据对数的概念,这个函数可以 写成对数的形式.就是 x = log2 y.提示学生逆 向思 考,用 x 表示自变量,y 表示函数,使其顺利得出新 的函数形式 y = log2 x,并辅助学生总结出对数函数 的概念,即为,一般地,当 a>0 且 a ≠1 时,函数 y = logax 叫做对数函数.随后教师指导学生结合指数函数 的定义域、值域逆向研究对数函数的定义域和值域.
概念是数学学科的基石,是学生深度理解数学 问题的关键.在高中数学教学中,教师要通过灵活多 样的教学方法,引导学生深化对数学概念的理解,从 而为学生的思维发展奠定坚实的基础.在上述案例 中,教师合理利用指数函数与对数函数这对互逆概 念设计教学,帮助学生理解对数函数的概念,使其学 会利用联系的观点分析问题,让学生认识到事物之 间能够相互转化,为学生后续思维能力的进一步优 化奠定了基础.
2 借助定义教学契机,养学生逆向思维
定义即为对于一种事物的本质特征或一个概念 的内涵和外延,进行确切而简要的说明,与概念相 比,意思、出处和侧重点均有所不同.在高中数学教 学中,教师可借助定义教学的契机展开逆向思维锻 炼.某些与定义直接相关的问题,条件与结论是相互 等价的,能够相互推导出来,让学生了解到定义不仅能 正向使用,也可逆向使用,借此培养学生的逆向思维.
在开展“集合”教学时,教师先带领学生学习集 合、子集、全集和补集等相关基础性知识,重点是定 义的描述和元素,结合韦恩图指引学生学习交集的 定义 : 一般地,由所有属于 A 且属于 B 的元素所组 成的集合,叫做 A 与 B 的交集,记作 A ∩B,读作“A 交 B”,即A∩B = {x |x∈A,且 x ∈B}.使学结合这一说 法给出并集的定义: 一般地,由所有属于A 或属于 B 的 元素组成的集合,叫做集合A 与 B 的并集,A 与 B 的并 集记作A∪B,读作“A 并B”,即A∪B = {x |x∈A,或x∈ B}.之后,教师组织学生进行逆命题和真命题的判断练 习,如: 当集合A 是集合 B 的子集时,A∩B = A,反过来 讲,当A∩B =A 时,集合A 就是集合 B 的子集.要求学 生模仿这样的说法自主设计命题,由同伴判断.
数学定义皆为高度概括和抽象的语句对数学问 题进行归纳.在教学中,教师要以此为契机,引导学 生深度融入定义概念,深刻理解和认识定义,特别是 借助问题的反复认知,使得学生把握定义的内在意 义,培养学生思维的灵活性和深刻性.在这一课的教 学中,教师在讲授基础性的定义知识过程中融入逆 向思维的培养,并结合举例说明,让学生也列举一些 相关例子,使其学会逆向思考和应用定义,锻炼了学 生的逆向思维能力.
3 强化公式应用练习,培养学生逆向思维
从数学视角来看,公式是用数学符号表示几个 量之间关系的式子,具有典型的普遍性特征,适用于 同类关系的所有问题.在高中数学公式教学中应当 突出双向性,教师既要指导学生通过常规思维正向 使用公式求解问题,还需强化公式的逆向应用训练, 使其慢慢形成逆向理解公式的思维,促使学生牢固掌握、深化记忆与灵活使用,最终产生融会贯通的效 果,这样才能真正实现对学生思维的灵活性和敏锐性 的培养,使学生具有发现的慧眼,捕获问题的本质.
以“三角函数”教学为例,该部分知识内容运用 得较为广泛,通常是考试考查的一个重点.由于有多 种三角函数公式的存在,包括正弦、余弦、正切、余切 等,所以对学生灵活运用公式的水平要求较高,不过 只要学生掌握公式的逆推能力,学习起来难度就不 是特别大.在学习完理论知识后,教师可设计练习 题,先引导学生直接应用公式变化来解题,之后,再 鼓励学生从逆向视角出发,运用逆向思维进行求解.
逆向思维需要学生拥有对数学知识的深刻认识 以及对数学关系的准确把握.公式是数学学科的典 型特征,是数学关系的高度浓缩.在数学公式教学 中,教师要着眼于公式的灵活应用,让学生学会举一 反三,把握公式的本质.在上述案例中,教师高度重 视公式的正向与逆向使用,让学生学会使用恰当的 方法解答练习题,使其意识到逆向思维是处理问题 的有效工具,通过加强练习培养学生的逆向思维.
4 教师发挥引导作用,培养学生逆向思维
教师是学生学习进程中的引路人.科学有效的 引导能够给学生的学习带来事半功倍的效果,促进 学生在轻松快乐中掌握知识,在不经意间掌握数学 思维的方法.在新时期教育背景下的高中数学教学中, 要想更好地培养学生的逆向思维,教师需要及时更新 教育理念,坚持“以生为本”原则,增强对学生逆向思维 的训练,使其数学思维变得更加深刻和敏锐.同时,高 中数学教师还应发挥自身引导作用,引领学生适当采 用分析法与反证法分析数学问题,培养学生的双向思 考能力,使其学会应用这两种逆向思维方式.
例如,在实施“解析几何”教学时,教师引用例 题 : 在平面直角坐标系 xOy 中,动点 P 到定点 F(0, 1) 的距离和 P 到定直线 x = -4 的距离之比为 1∶ 2, 求动点 P 的轨迹 C 的方程.如果轨迹 C 上的动点 N 到定点 M(m,0) (0 <m<2) 的距离的最小值是 1,求 m 的值.第一问较为简单,学生能够轻松推导出动点P 的轨迹方程是
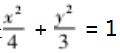
.处理第二问时,学生通常只考虑到 0 <4m <2 这一种情况,容易把 4m >2 的情况漏掉,此时,教师就需要引领学生结合结论把 公式逆向推理,使其发现其中的问题.让学生分两种 情况进行讨论 : 当 0 <4m <2 时,由 | MN | 2 = 1,通过计算能够得出 m =
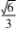
,代入公式后发现 x >2,超出讨论区间,要把这个值舍去 ; 当 4m >2 时,当 x = 2 时,| MN | 2 取最小值 1,可求得 m = 1 或 m = 3 ( 舍 去).综上,m = 1.
学生思维本领的发展是一个潜移默化的渐进过 程,学生思维能力的提升不是一蹴而就的.在此过程 中,既需要学生在平时的学习中不断总结,不断升 华,更离不开教师的悉心指导.为此,在平时 的教 学中,教师应针对学生的学习实际,有 意识地培 养学生的数学思维,尤其是借助一些典型的数学 问题,挖掘学生的思维潜能,让学生有豁然开朗 之感,促进学生思维的顿悟.在上述教学案例中, 教师极力发挥出自身的引导作用,提示学生采用 逆向推理,帮助学生走出思维 的 困境,产生“拨开 云雾见日月”之感.
5 积极开展解题训练,培养学生逆向思维
在高中数学教学中,解题训练是不可或缺的一 个重要环节,既能检测学生对理论知识和解题方法 的掌握情况,还可以锻炼学生的解题技巧,使其掌握 更多窍门,从而正确、快速地处理数学试题.因此,高 中数学教师需积极开展解题训练活动,指引学生采 用逆向思维分析和解题,使其把复杂、特殊、抽象的 问题变得简便、一般和具体.
在“数列”教学中,教师可设置这样一道数学试题 : 已知 a1 = 3,an + 1 = a,n=N* ,求 an 的值.本道题目主要考查学生对数列知识的掌握情况.教师可先 要求学生认真阅读题目内容,找出已知信息和所求 问题,使其尝试从逆向视角切入,结合函数相关知识 求解.具体解题过程如下 : 结合题目中给出的已知条件 an + 1 = a,能够将其转变成函数关 系 式,即 为f(n + 1) =f 2 (n) ,得到这个式子 以后,教师可 以让 学生联想到需要使用什么方式把函数式继续推导下 去,使其运用函数概念、公式等知识,套入公式后得到f( n) = f 2 ( n -1 ) ,然后继续推导得出f (2 ) = f 2 ( 1) ,经过一系列计算得到f ( n) = [f ( 1) ]2n-1 = 32n-1 也就是说 an = 32n-1 .
数学学习离不开解题,解题既是学生数学学习 的重要内容,也是优化学生思维品质的重要引擎,解 题能力与学生的思维品质的培养可谓相辅相成.学 生的学习归根结底要落脚于学生的解题能力.为此, 在平时的数学教学中,教师一方面要通过庖丁解牛 式的细致讲解,帮助学生厘清数学知识的脉络,更重 要的是指导学生学会解题,善于解题,不断提升学生 的数学解题能力.在平时的教学中,教师要通过精心 设计解题活动,通过展示、分享、分析、比较,不断凸 显学生解题过程中的得与失、优与劣,并从思维的品 质上给予评价.上述案例中,教师积极设计解题训练 活动,为学生提供和制造更多运用逆向思维的机会, 使其获得解决问题的新途径,能够快捷、高效地解答 试题,改善学生的逆向思维水平,同时更提升了学生 的数学解题能力.
总之,数学思维是学生数学学习的重要内容,是 提升学生数学学习质效的关键内在因素.逆向思维 更是学生思维品质中的关键组成.在高中数学教学 实践中,教师应意识到培养逆向思维的重要性与价 值,在日常教学中要善于把握契机,从概念、定义、公 式和解题等多个环节切入,全方位培养学生的逆向 思维能力,使其深化理解数学理论知识,让学生形成 简便、有效的解题思路.
参考文献 :
[1]瞿冲.论高中数学教学中学生的逆向思维培养 [J].高中数理化,2021 (S01) : 76 .
[2]王万仓.数学教学中学生逆向思维能力培养研 究[J].成才之路,2020(17) : 50-51 .
[3]周青云.培养学生数学逆向思维的有效途径 [J].吉林教育,2018(18) : 60-61 .
[4] 张元亮.高中数学教学中培养学生逆向思维能力的办法[J].数理化解题研究,2017 (27) : 17-1.
[5]史姗珊.高中数学教学中学生逆向思维能力的 培养探讨[J].考试周刊,2017 (A1) : 100 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/74985.html

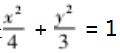 .处理第二问时,学生通常只考虑到 0 <4m <2 这一种情况,容易把 4m >2 的情况漏掉,此时,教师就需要引领学生结合结论把 公式逆向推理,使其发现其中的问题.让学生分两种 情况进行讨论 : 当 0 <4m <2 时,由 | MN | 2 = 1,通过计算能够得出 m =
.处理第二问时,学生通常只考虑到 0 <4m <2 这一种情况,容易把 4m >2 的情况漏掉,此时,教师就需要引领学生结合结论把 公式逆向推理,使其发现其中的问题.让学生分两种 情况进行讨论 : 当 0 <4m <2 时,由 | MN | 2 = 1,通过计算能够得出 m = 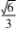 ,代入公式后发现 x >2,超出讨论区间,要把这个值舍去 ; 当 4m >2 时,当 x = 2 时,| MN | 2 取最小值 1,可求得 m = 1 或 m = 3 ( 舍 去).综上,m = 1.
,代入公式后发现 x >2,超出讨论区间,要把这个值舍去 ; 当 4m >2 时,当 x = 2 时,| MN | 2 取最小值 1,可求得 m = 1 或 m = 3 ( 舍 去).综上,m = 1.
